Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
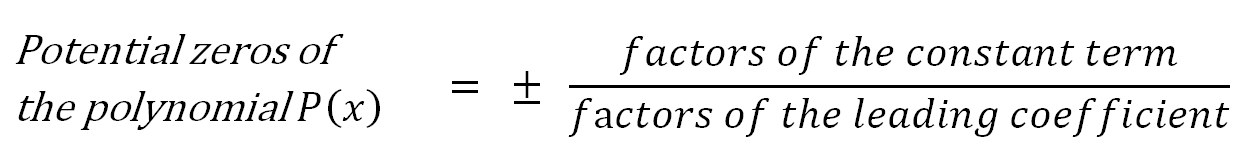
Introduction to the Rational Zero Theorem
The rational zero theorem, also known as the rational zero test or rational root test, is a fundamental concept in algebra that helps in finding zeros of polynomial functions. This powerful theorem provides a systematic approach to identifying potential rational roots of a polynomial equation. Our introduction video offers a comprehensive overview of this essential mathematical tool, making it easier for students to grasp its significance and application. By understanding the rational zero theorem, learners can efficiently narrow down the possible solutions of complex polynomial equations, saving time and effort in problem-solving. This theorem is particularly useful in higher-level mathematics and various scientific fields where polynomial functions play a crucial role. As we delve deeper into the rational zero theorem, you'll discover how it simplifies the process of finding roots and enhances your overall understanding of polynomial behavior.
Here are some frequently asked questions about the Rational Zero Theorem:
1. What is the Rational Zero Theorem?
The Rational Zero Theorem states that if a polynomial equation with integer coefficients has a rational solution, it will be in the form ±p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.
2. How do you identify the possible rational zeros of a polynomial equation?
To identify possible rational zeros, list all factors of the constant term (including both positive and negative) and divide them by all factors of the leading coefficient. This gives you a list of potential rational zeros to test.
3. What is the difference between real zeros and rational zeros?
Real zeros include all solutions on the real number line, while rational zeros are specifically those that can be expressed as a fraction of two integers. All rational zeros are real, but not all real zeros are rational (e.g., irrational numbers like 2).
4. Why does the Rational Zero Theorem not always work?
The theorem only provides potential rational zeros. It doesn't guarantee that any of these are actual zeros, nor does it help find irrational or complex zeros. Some polynomials may have no rational zeros at all.
5. How do you know if a zero is rational?
A zero is rational if it can be expressed as a fraction of two integers. After identifying potential zeros using the Rational Zero Theorem, you need to test each one in the original polynomial equation to confirm if it's an actual zero.
The Rational Zero Theorem is a powerful tool in algebra, but to fully grasp its concepts and applications, it's crucial to have a solid foundation in several prerequisite topics. Understanding these fundamental concepts will not only make learning the Rational Zero Theorem easier but also enhance your overall mathematical skills.
One of the key prerequisites is determining the equation of a polynomial function. This skill is essential because the Rational Zero Theorem deals with polynomial equations. Knowing how to identify and work with the factors of leading coefficients is particularly important in this context.
Another crucial concept is the ability to determine square roots of rational numbers. This skill is fundamental when working with rational roots, which are at the core of the Rational Zero Theorem. Being comfortable with rational numbers and their properties will greatly facilitate your understanding of the theorem.
Polynomial synthetic division is another important prerequisite. This efficient method of dividing polynomials is often used in conjunction with the Rational Zero Theorem to test potential zeros of a polynomial function. Similarly, polynomial long division is an alternative method that serves the same purpose and is equally important to master.
The Intermediate Value Theorem is a more advanced concept that relates to the Rational Zero Theorem. While not directly used in the theorem, understanding this principle can provide valuable insights into the behavior of polynomial functions and their roots.
Lastly, familiarity with using the quadratic formula to solve quadratic equations is beneficial. Although the Rational Zero Theorem applies to polynomials of any degree, quadratic equations are the simplest non-linear polynomials, and understanding how to solve them provides a good foundation for working with higher-degree polynomials.
By mastering these prerequisite topics, you'll be well-prepared to tackle the Rational Zero Theorem. Each concept builds upon the others, creating a comprehensive understanding of polynomial functions and their properties. This knowledge not only aids in learning the theorem itself but also enhances your problem-solving skills in algebra and higher-level mathematics. Remember, a strong foundation in these basics is key to success in more advanced mathematical concepts.



