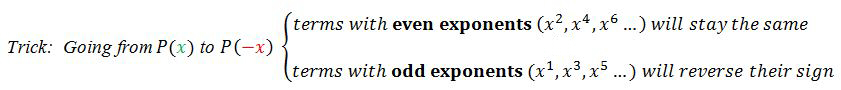Sign In
Sign Up
flag-us

Descartes' Rule of Signs: Unraveling Polynomial Root Mysteries
Discover how Descartes' Rule of Signs revolutionizes polynomial analysis. Learn to predict root types, complement the Fundamental Theorem of Algebra, and gain deeper insights into polynomial behavior.

  1. Intros0/2 watched
  2. Examples0/4 watched
  3. Practice0/12 practiced
  1. 0/2
  2. 0/4
  3. 0/12
Now Playing:Descartes rule of signs – Example 0a
Intros
0/2 watched
  1. Introduction to Descartes' Rule of Signs
  2. Introduction to Descartes' Rule of Signs
    Fundamental Theorem of Algebra VS. Descartes' Rule of Signs
  3. Introduction to Descartes' Rule of Signs
    Descartes' Rule of Signs – explained.
    exercise: Use Descartes' Rule of Signs to determine the possible combinations of roots of:
    P(x)=2x6−7x5+x4+5x3−6x2−10P(x)=2x^6-7x^5+x^4+5x^3-6x^2-10
Examples
0/4 watched
  1. Use Descartes' Rule of Signs to Determine the Number of Positive and Negative Roots
    Use Descartes' Rule of Signs to determine the possible number of positive roots and negative roots:
    1. P(x)=4x+9x6−5x2−10x7+6x3−8x5−7x4+3 P(x)=4x+9x^6-5x^2-10x^7+6x^3-8x^5-7x^4+3

      0/4

    2. P(x)=x4−5x2−6x P(x)=x^4-5x^2-6x (note: NO constant term!!)

      0/4

Practice
0/12
Descartes Rule Of Signs 1a
Polynomial long division
Jump to:NotesConceptFAQsPrerequisites
Notes
Descartes' Rule of Signs For a polynomial P(x)P(x):
∙\bullet the number of positive roots = the number of sign changes in P(x)P(x), or less than the sign changes by a multiple of 2.
∙\bullet the number of negative roots = the number of sign changes in P(−x)P(-x), or less than the sign changes by a multiple of 2.

Note: Before applying the Descartes' Rule of Signs, make sure to arrange the terms of the polynomial in descending order of exponents.

trick of Descates' rule of signs
Concept

Introduction to Descartes' Rule of Signs

Descartes' Rule of Signs is a powerful mathematical theorem that provides insights into the nature of polynomial roots. This rule, introduced in our video, offers a method to determine the possible number of positive and negative real roots of a polynomial equation. It extends the Fundamental Theorem of Algebra by providing more specific information about root distribution. The rule states that the number of positive real roots of a polynomial equation is either equal to the number of sign changes between consecutive nonzero coefficients, or is less than it by an even number. Similarly, the number of negative real roots is the number of sign changes after multiplying the coefficients of odd-power terms by 1, or fewer by an even number. While not determining exact root values, Descartes' Rule of Signs is invaluable for analyzing polynomial behavior and serves as a cornerstone in advanced algebra and calculus, bridging theoretical concepts with practical problem-solving in various mathematical and scientific fields.

FAQs

Q1: What is Descartes' Rule of Signs?
A1: Descartes' Rule of Signs is a mathematical theorem that helps determine the possible number of positive and negative real roots in a polynomial equation. It states that the number of positive real roots is either equal to the number of sign changes between consecutive nonzero coefficients or less than it by an even number. For negative roots, the same principle applies after multiplying the coefficients of odd-power terms by -1.

Q2: How does Descartes' Rule of Signs relate to the Fundamental Theorem of Algebra?
A2: While the Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n complex roots (counting multiplicity), Descartes' Rule of Signs provides more specific information about the nature of real roots. It complements the Fundamental Theorem by offering insights into the distribution of positive and negative real roots, which the Fundamental Theorem doesn't address directly.

Q3: Can Descartes' Rule of Signs determine the exact number of roots?
A3: No, Descartes' Rule of Signs provides an upper bound on the number of positive and negative real roots, not the exact count. The actual number of roots can be equal to the number of sign changes or less than it by an even number. For precise root determination, additional methods or theorems are needed.

Q4: How do you apply Descartes' Rule of Signs to find negative roots?
A4: To find negative roots, you first replace x with -x in the original polynomial. Then, you apply the same sign change counting process to this new polynomial. The number of sign changes in this transformed polynomial indicates the possible number of negative roots in the original polynomial.

Q5: What are the limitations of Descartes' Rule of Signs?
A5: Descartes' Rule of Signs has several limitations: it only provides information about real roots, not complex ones; it gives an upper bound rather than an exact count of roots; and it doesn't provide information about root values or multiplicity. Additionally, for polynomials with coefficients that are not real numbers, the rule may not be directly applicable.

Prerequisites

Understanding Descartes' rule of signs is a crucial step in advanced algebra, but it requires a solid foundation in several key areas. One of the most fundamental prerequisites is the ability to determine the equation of a polynomial function. This skill is essential because Descartes' rule deals directly with polynomial equations and their roots.

The Fundamental Theorem of Algebra is another critical concept to grasp. It states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This theorem forms the basis for understanding why Descartes' rule works and how it relates to the number of real roots in a polynomial.

When applying Descartes' rule, it's important to be familiar with the nature of real roots of polynomials. This knowledge helps in interpreting the results of the rule and understanding its limitations. Similarly, understanding characteristic polynomial roots, including complex roots, provides a more comprehensive view of polynomial behavior.

The concept of even and odd exponents plays a significant role in Descartes' rule. The rule relies on analyzing the signs of coefficients in a polynomial, and the behavior of even and odd exponents directly influences these signs and the potential number of positive and negative roots.

Lastly, a strong understanding of quadratic equation roots provides a solid foundation for applying Descartes' rule to higher-degree polynomials. The principles learned from quadratic equations, such as the relationship between the discriminant and the nature of roots, extend to more complex polynomials.

By mastering these prerequisite topics, students will be well-equipped to understand and apply Descartes' rule of signs effectively. This rule is not just an isolated concept but a powerful tool that builds upon fundamental algebraic principles. It allows for quick estimation of the number of positive and negative real roots in a polynomial equation without solving it, making it an invaluable technique in advanced algebra and calculus.

As students progress in their mathematical journey, they'll find that Descartes' rule of signs connects various aspects of algebra, from basic polynomial manipulation to complex root analysis. This interconnectedness highlights the importance of building a strong foundation in these prerequisite topics, enabling a deeper appreciation and more effective application of Descartes' rule in solving complex mathematical problems.