Waves in two dimensions

In this lesson, we will learn:

• Reflection of two-dimensional waves
• Recreation of two-dimensional waves
• Diffraction of two-dimensional waves

Notes:

• Waves moving along rope or spring are mechanical waves that move only in one dimension.
• Waves on the surface of water or sound waves move in two dimensions.
• Similar to one one-dimensional waves, two-dimensional waves get both reflected and refracted.
• As waves from one medium to another, partially reflect and partially refract.
• Properties of two-dimensional waves can be shown using a ripple tank which contains a thin layer of water. Vibrating boards produce wave pulses with constant frequency. The lamp above the tank produces shadows below the tank to show the exact location of crest and troughs.
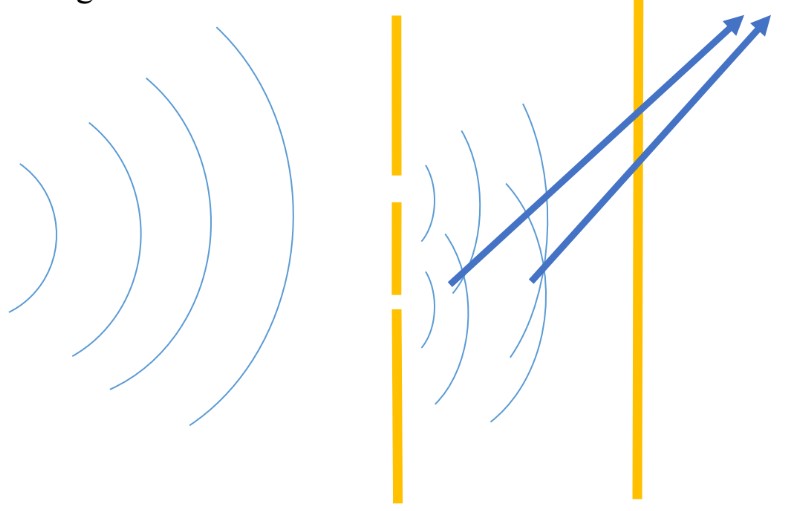
• Pulses travelling towards a rigid barrier get “Reflected”.
• Pulses reaching a boundary might change direction or get “Refracted”.
• Pulses passing through a small hole, spread or get “Diffracted”.

Reflection

• A ray diagram model is used to study the reflection of two-dimensional waves.
• A ray is a line drawn at right angles to the crests of the waves.

Key terms using a ray model to study reflection:

Incident Ray: An arrow pointing towards the boundary

Point of incidence: Point where incident ray meets the boundary

Reflected Ray: An arrow pointing away from the boundary

A straight line: showing the direction of the barrier

Normal: A line drawn perpendicularly to the barrier at point of incidence

Angle on incidence ($< i$ ): The angle between incident ray and NORMAL

Angle of reflection ($< r$ ): The angle between reflected ray and NORMAL

Barrier

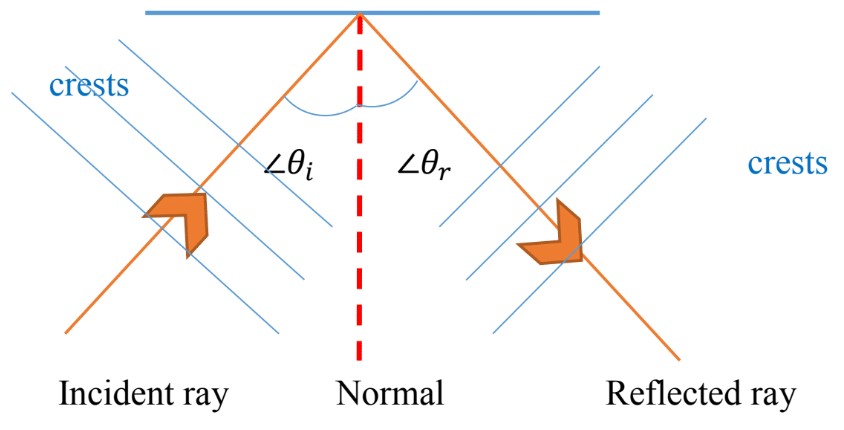
• According to the law of reflection; angle of incidence is equal to angle of reflection ( $\angle \theta_{i} = \angle \theta_{r}$ )
• Upon reflection Speed, Wavelength, and Frequency do NOT change.

Refraction

Key terms using ray model to study refraction:

Incident Ray: An arrow pointing towards the boundary

Point of incidence: Point where incident ray meets the boundary

Refracted Ray: An arrow pointing away from the boundary in the other medium

A straight line: showing the direction of the barrier

Normal: A line drawn perpendicularly to the barrier at point of incidence

Angle on incidence ($\angle \theta_{i}$): The angle between incident ray and NORMAL

Angle of refraction ($\angle \theta_{r}$): The angle between refracted ray and NORMAL

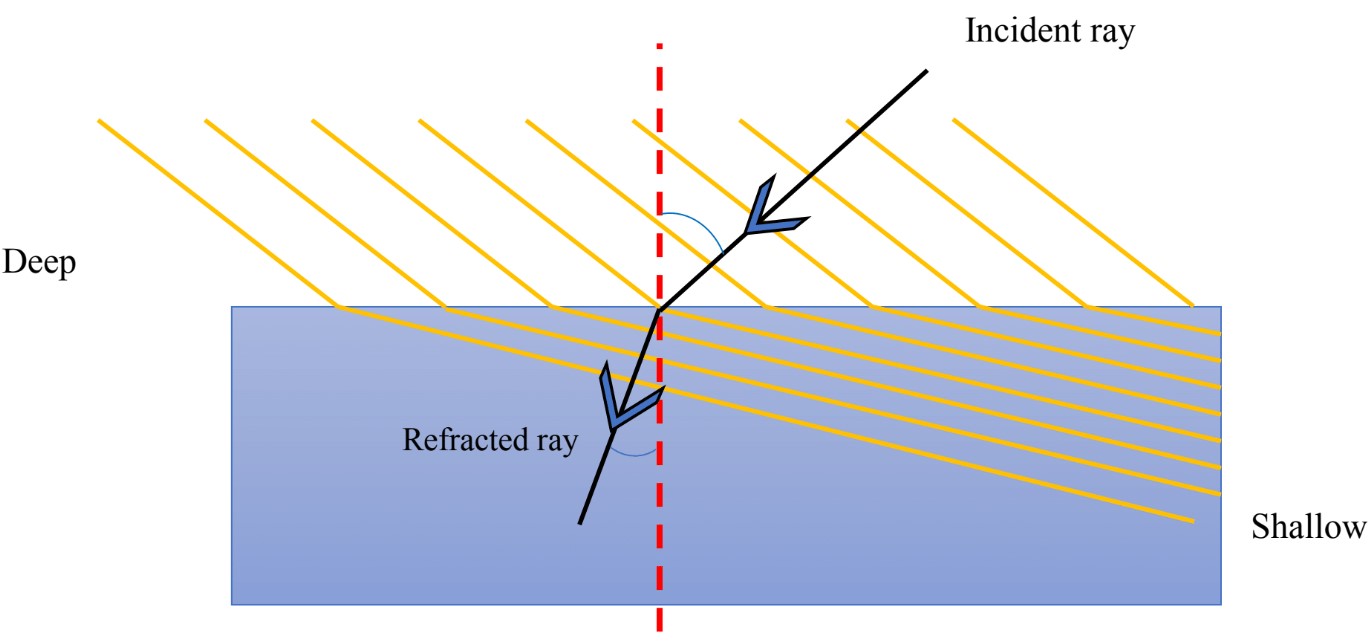
• As waves move from one medium to another with different densities (shallow or deep), they get refracted, change direction at the boundary.
• Shallow medium: Lower Velocity, Shorter Wavelength, Same Frequency
• Deep medium: Higher Velocity, Longer Wavelength, Same Frequency

Diffraction of waves

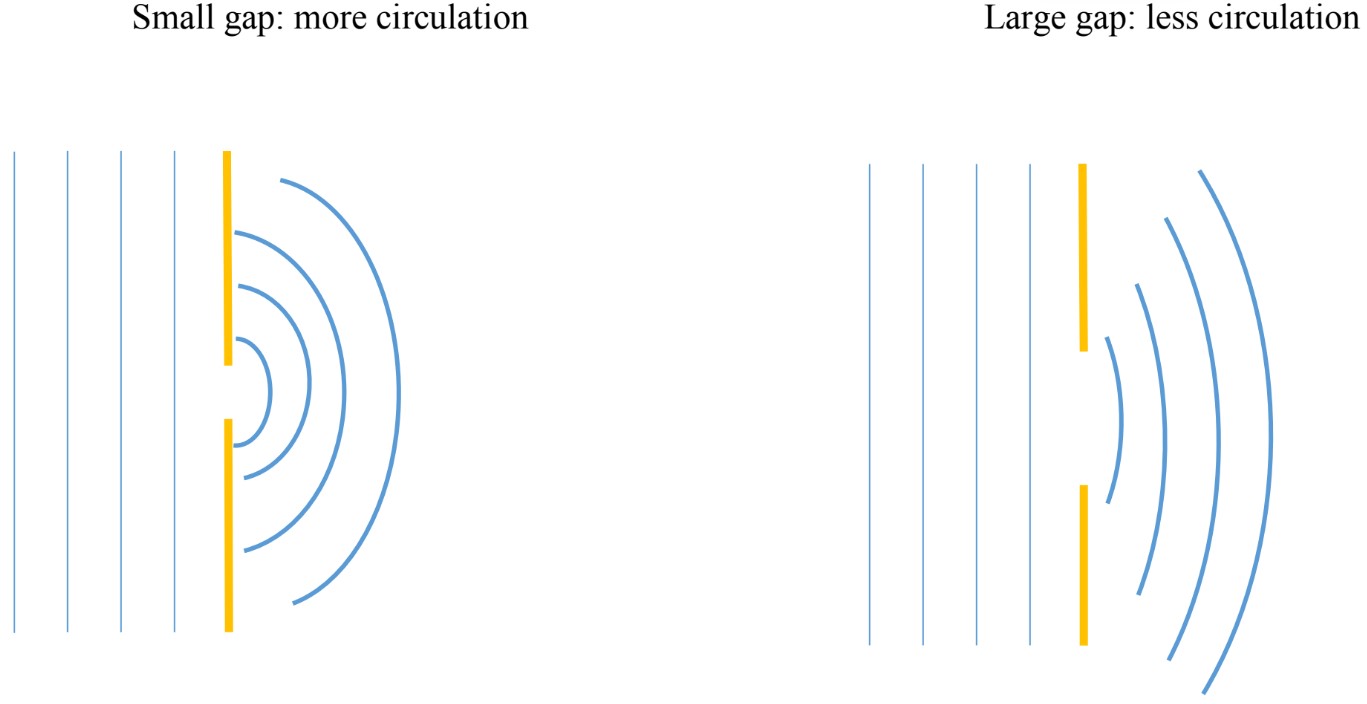
• The process of diffraction is the spreading of waves through a small gap, waves circulating out of the gap.
• Size of the gap affects the shape of the diffracted wave;

Interference of diffracted waves

• Diffracted waves interfere with each other producing constructive and destructive interface.
• The result of light interference through small gaps can be collected on a screen, light and dark fringes are seen on the screen. Points where waves interference constructively