Vector operations in two dimensions

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

Get the most by viewing this topic in your current grade. Pick your course now.

?
Intros
Lessons
  1. Introduction to vector operations in two dimensions
?
Examples
Lessons
  1. Perform tip-to-tail addition in two dimensions

    A student arrives at school and from the entrance walks 20 m north to go to English. After, they walk 30 m east to physics class. What is their overall displacement? Answer with a vector diagram and a vector equation that describes the displacements.

    1. Solve vector additions graphically

      Solve the following vector equations graphically:

      i. Δd⃗1+Δd⃗2=Δd⃗res\Delta \vec{d}_{1} + \Delta \vec{d}_{2} = \Delta \vec{d}_{res}

      PHYS 1 3 2a

      ii. v⃗1+v⃗2=v⃗res\vec{v}_{1} + \vec{v}_{2} = \vec{v}_{res}

      PHYS 1 3 2b

      iii. A⃗+B⃗+C⃗=D⃗\vec{A} + \vec{B} + \vec{C} = \vec{D}

      PHYS 1 3 2c
      1. Solve vector subtraction, multiplication, and division graphically

        Solve the following vector equations graphically:

        i. Δd⃗1−Δd⃗2=Δd⃗res\Delta \vec{d}_{1} - \Delta \vec{d}_{2} = \Delta \vec{d}_{res}

        PHYS 1 3 3b

        ii. 2v⃗1+0.2v⃗2=v⃗res2\vec{v}_{1} + 0.2 \vec{v}_{2} = \vec{v}_{res}

        PHYS 1 3 3c

        iii. A⃗−2B⃗−C⃗2=D⃗\vec{A} - 2\vec{B} - \frac{\vec{C}}{2} = \vec{D}

        PHYS 1 3 3c
        1. Write and draw the angles of vectors relative to compass directions PHYS 1 3 4

          i. Write the vector using vector notation

          ii. Draw the vector C⃗\vec{C} = 2.5 m [40° S of E] on a set of compass axes.

          1. Calculate two dimensional displacement with Trigonometry

            A car drives at 13.8 m/s [W] for 115 s. It then turns left and travels south at 19.4 m/s for 135 s. Find the displacement of the car from its starting position.

            Topic Notes
            ?
            In this lesson, we will learn:
            • How to do addition, subtraction, multiplication and division on vectors in two dimensions
            • How to describe the angles of two dimensional vectors
            • How to solve for the angle and magnitude of two dimensional vectors with trigonometry.

            Notes:

            • When adding, subtracting, multiplying, and dividing vectors in two dimensions, the same rules are followed as in one dimensional problems:
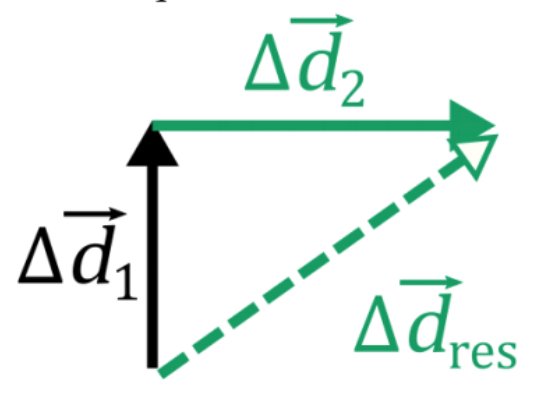
              • When vectors are added, the vector diagram is drawn by tip-to-tail addition. To add A⃗\vec{A} and B⃗\vec{B}, draw the vector A⃗\vec{A}, then starting at the tip of A⃗\vec{A} draw B⃗\vec{B}. The tail of B⃗\vec{B} connects to the tip of A⃗\vec{A}.
              • Taking the negative of a vector "flips" the vector to point in the opposite direction, while keeping the same magnitude.
              • Multiplying or dividing a vector by a positive scalar changes the magnitude of the vector, while keeping the same direction.
            • The graphical solution to a vector problem in two dimensions can make a vector triangle that can be solved using trigonometry.
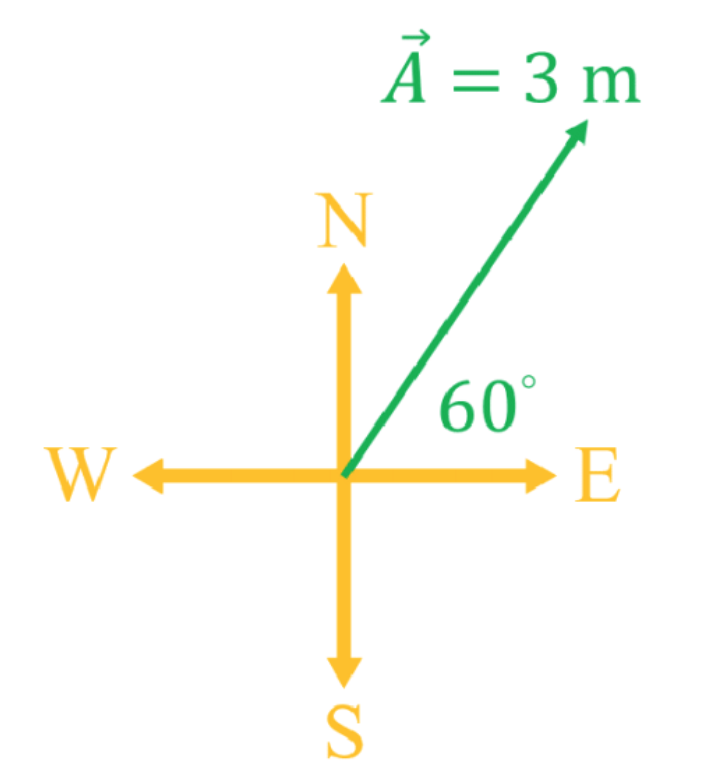
            • In this course we will be using navigational notation to specify the angles of vectors, which also called to compass notation when compass directions are used in the problem. Some examples of this notation:
              • To specify a displacement of 1 m directly northwest, write 1 m [45° N of W].
              • To specify a velocity that that is 1 m/s at an angle of 30° above the ground, write 1 m/s [30° above horizontal]
            Right Triangle Trigonometric Equations

            sin⁡(θ)=opp.hyp.\sin(\theta) = \frac{opp.}{hyp.}

            cos⁡(θ)=adj.hyp.\cos(\theta) = \frac{adj.}{hyp.}

            tan⁡(θ)=opp.adj.\tan(\theta) = \frac{opp.}{adj.}

            a2+b2=c2a^{2}+b^{2}=c^{2} (Pythagorean theorem)

            θ\theta: angle, in degrees (°)

            opp.opp.: side opposite angle

            adj.adj.: side adjacent angle

            hyp.hyp.: hypotenuse of triangle (longest side, side opposite 90° angle)

            aa and bb: non-hypotenuse sides of triangle

            cc: hypotenuse of triangle