The periodic nature of SHM and simple pendulum

In this lesson, we will learn:

• The nature of the periodic motion
• The graph analysis of the periodic motion
• Simple Pendulum

Notes:

• If each vibration (the back and forth motion) takes the same amount of time, then the motion is Periodic.
• To discuss the period motion we need to define the following terms;
• Cycle; a complete to-and-fro movement.
• Amplitude; maximum displacement, the greatest distance from the equilibrium position.
• Period; time taken for one complete oscillation.
• Frequency; number of oscillations in one second.

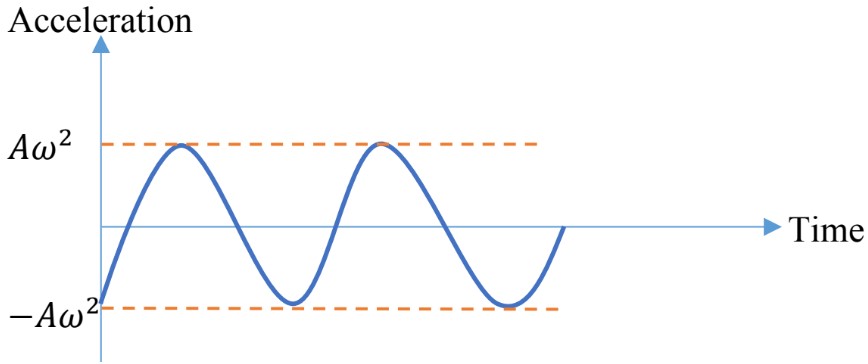
• The following equations represent the mathematical relationship between frequency and period of motion;

$\large f = \frac{1}{T} \quad$ and $\quad\large T = \frac{1}{f}$

Position as a Function of Time
Since the motion is considered as a periodic motion, we would be able to plot position Vs. time graph.



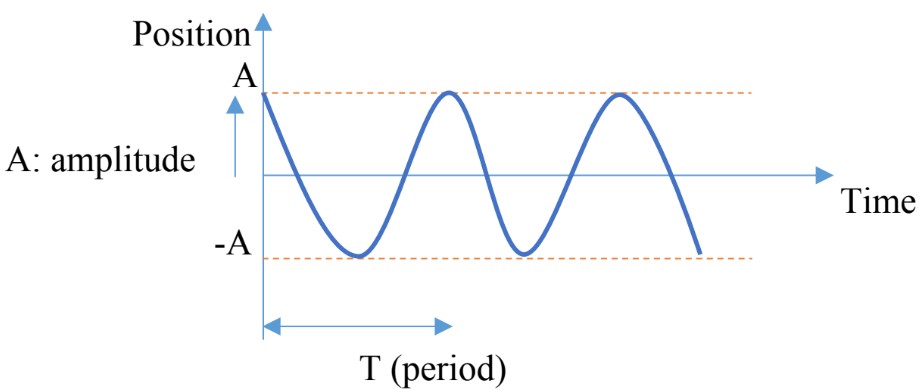
Looking at the graph we can refer to it as the cosine function, since at t = 0 the position is maximum;

$x \, (t) = Acoswt$

$w =$ angular velocity 
$w = 2 \pi f = 2 \pi / T$

$x \, (t) = Acos(2 \pi f t) = Acos$ $\large (\frac{2 \pi t}{T})$

• For one complete cycle,

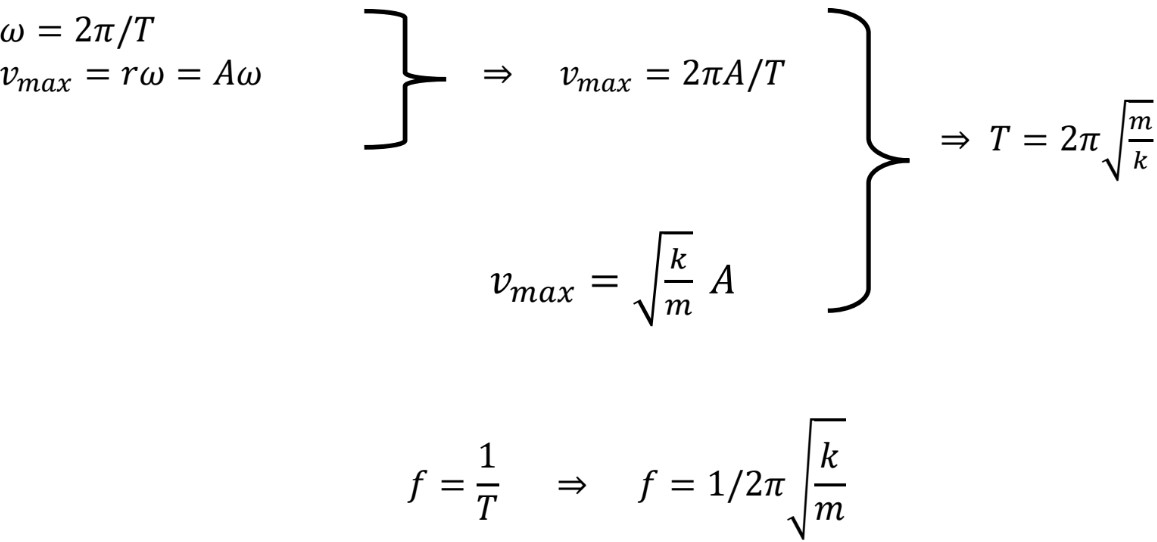
Velocity as a Function of Time

• Velocity is defined as the derivative of position with respect to time,

$v =$ $\large \frac{dx}{dt}$ $=$ $\large \frac{d}{dt}$ $(Acoswt) = - Aw (sinwt)$

Since the Velocity is the sine function of time, at $t = 0, V = 0$, therefore; the graph starts at zero.



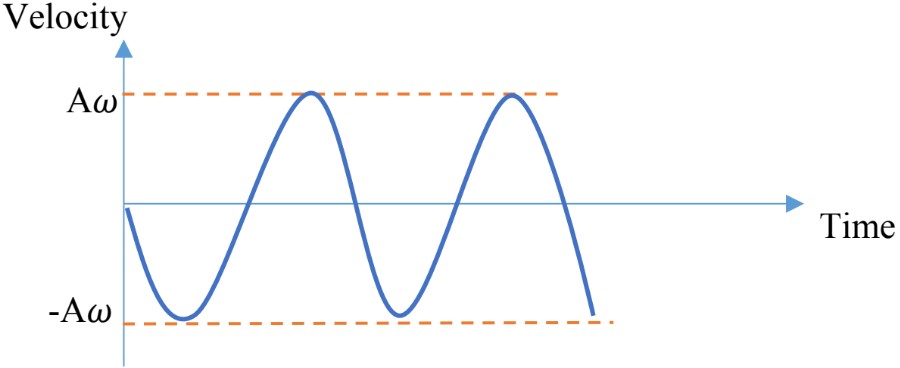
Acceleration as a Function of Time

• Acceleration is defined as the derivative of velocity with respect to time,

$a =$ $\large \frac{dv}{dt}$ $=$ $\large \frac{d}{dt}$ $(-Awsinwt) = - Aw^{2} \, (coswt)$



$a =$ $\large \frac{F}{m}$ $= -$ $\large \frac{kx}{m}$ $=-$ $\large (\frac{kA}{m})$ $coswt = - a_{max} coswt$
$\Rightarrow a_{max} =$ $\large \frac{kA}{m}$
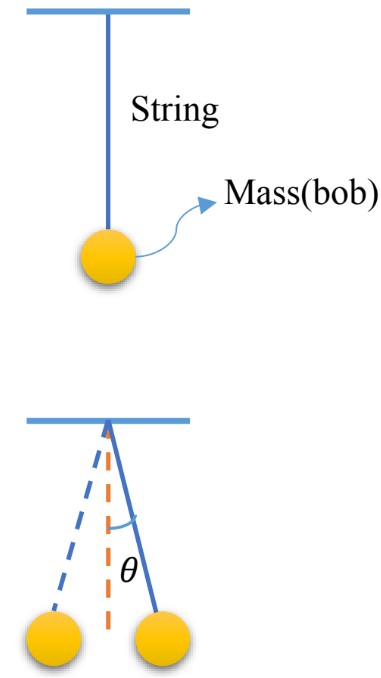
Simple Pendulum

• A simple pendulum is a small mass attached to the end of a string.
• The pendulum swings back and forth, ignoring the air resistance, it resembles simple harmonic motion.

Let’s apply the simple harmonic oscillator to the case of the simple pendulum;

$x(t) = Acos$$\large (\frac{2 \pi}{T} \, t)$

In the case of simple pendulum;
$A$; is the maximum angular displacement, $\theta _{max}$
$x$; is the angle the pendulum is at; the angle is measured from the equilibrium positon (the vertical position),$\theta$.

$\theta \, (t) = \theta_{max} cos$ $\large (\frac{2 \pi}{T}\, t)$

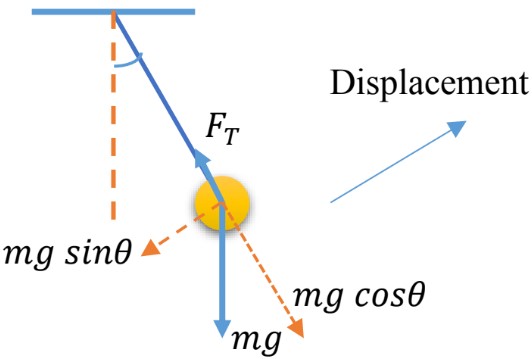
• The restoring force is opposite to the displacement and is equal to the component of the weight;


$F = - mgsin \theta$

• In this case, the motion is considered to be simple harmonic motion if the angle is less than 15°, for small angles, $\sin \theta \approx \theta$;

Form Hooke’s law;
$F = - Kx$ $\qquad \qquad \qquad \qquad \qquad \qquad \Rightarrow K =$ $\large \frac{mg}{L}$
$F \approx -$ $\large \frac{mgx}{L}$

We know from spring- mass system;


$T = 2 \pi \, \sqrt{\frac{m}{k}} \, \Rightarrow \, T = 2 \pi \, \sqrt{\frac{m}{mg\, / \, L} } \, \Rightarrow \, T = 2 \pi \, \sqrt{\frac{L}{g}}$

and $f =$ $\large \frac{1}{2 \pi}$ $\sqrt{\frac{g}{L}} \enspace K = \frac{mg}{L}$