Sign In
Sign Up
flag-us

Mastering Tension and Pulley Problems: Calculations and Solutions
Unlock the secrets of tension and pulley systems! Learn step-by-step methods to calculate tension forces, solve complex pulley problems, and apply your knowledge to real-world scenarios.

Get the most by viewing this topic in your current grade. Pick your course now.

Now Playing:Tension and pulley problems – Example 0a
Intros
  1. Introduction to tension:
  2. Introduction to tension:
    What is tension? How to calculate tension using Newton's second law.
  3. Introduction to tension:
    Tension force at either end of a rope
Examples
  1. Calculating tension using Newton's second law

    A train toy is made up of three carts of different masses connected by pieces of string. If string A is pulled with 7.05 N [right], find the tension in strings A, B, and C.

    PHYS 3 7 1
    Newton's first law of motion
    Jump to:NotesConceptFAQsPrerequisites
    Notes
    In this lesson, we will learn:
    • What is tension?
    • How to calculate tension
    • Problem solving with tension

    Notes:

    • Tension is the force of a rope (or string, cable, etc.) pulling on an object.
      • Tension is always a pulling force: a rope can't push!
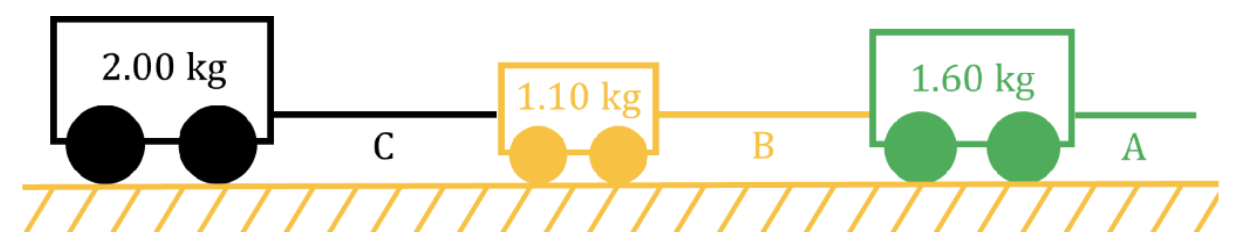
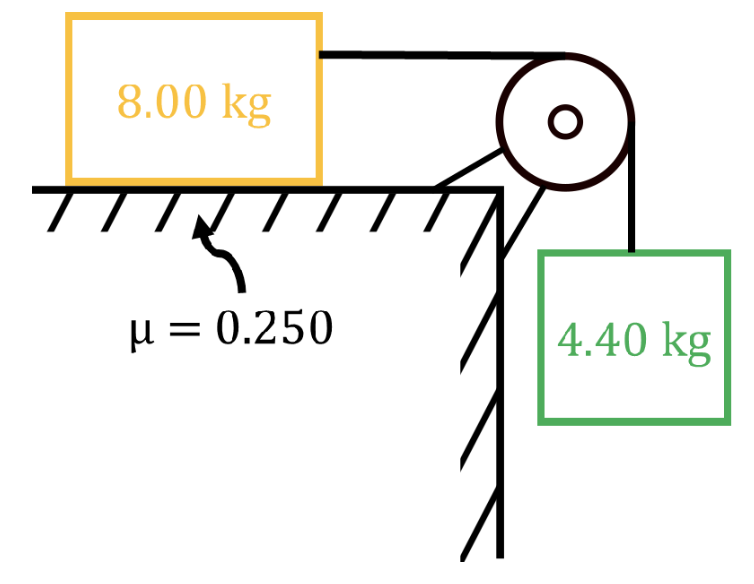
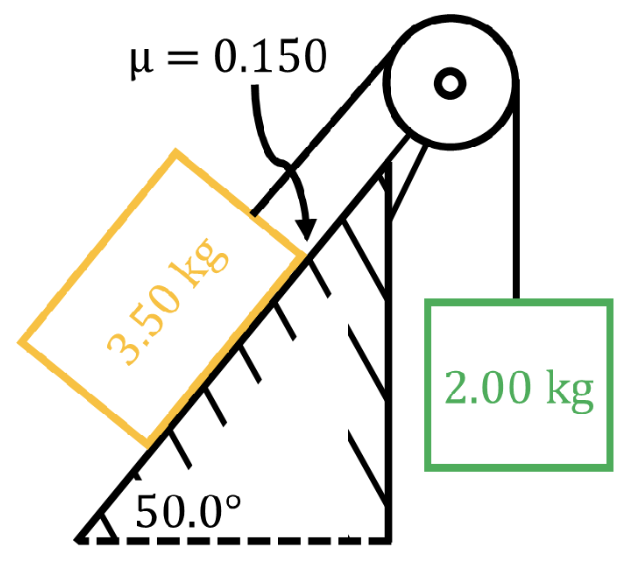
    • There is no formula for tension. Tension force acting on an object must be calculated from Newtons' second law.
    • If the rope is assumed to be massless and non-stretchy, then the pulling force at either end of the rope must be equal in magnitude.
    Newton's Second Law

    ΣF⃗=F⃗net=ma⃗\Sigma \vec{F} = \vec{F}_{net} = m\vec{a}

    ΣF⃗:\Sigma \vec{F}: sum of all forces, in newtons (N)

    F⃗net:\vec{F}_{net}: net force, in newtons (N)

    m:m: mass, in kilograms (kg)

    a⃗:\vec{a}: acceleration, in meters per second squared (m/s2)(m/s^{2})


    Newton's Third Law

    For object A exerting a force on object B:

    F⃗AonB=−F⃗BonA\vec{F}_{A on B} = - \vec{F}_{B on A}

    F⃗AonB:\vec{F}_{A on B}: force A is exerting on B, in newtons (N)

    F⃗BonA:\vec{F}_{B on A}: force B is exerting on A, in newtons (N)


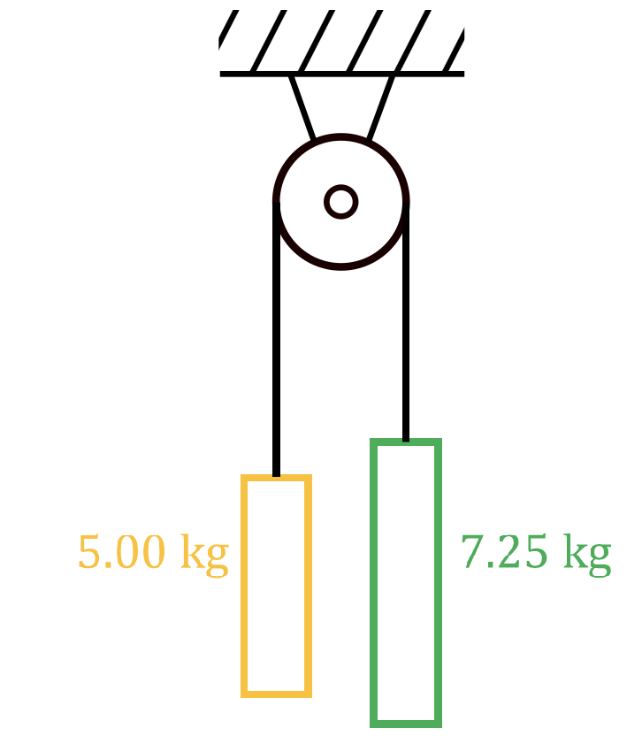
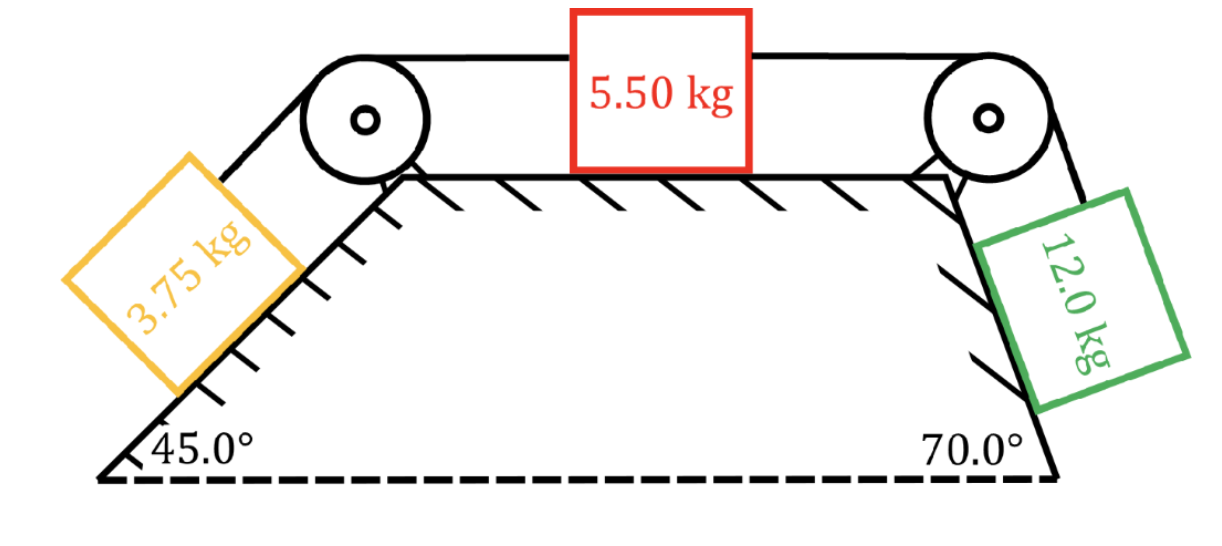
    Atwood Machine Equation

    a=g(m1−m2)(m1+m2)a = g\frac{(m_{1}-m_{2})}{(m_{1}+m_{2})}

    a:a: acceleration of masses, in meters per second squared (m/s2)(m/s^{2})

    g:g: acceleration due to gravity, in meters per second squared (m/s2m/s^{2})

    m1:m_{1}: mass of first hanging mass, in kilograms (kg)

    m2:m_{2}: mass of second hanging mass, in kilograms (kg)

    Concept

    Introduction to Tension and Pulley Problems

    Welcome to the fascinating world of tension and pulley problems! These concepts are fundamental in physics and engineering, playing a crucial role in understanding how forces interact in various mechanical systems. Our introduction video serves as an excellent starting point, providing a clear and concise overview of the key principles involved. By watching this video, you'll gain valuable insights into how tension works in ropes and cables, and how pulleys can be used to manipulate forces. We'll explore real-world applications, from simple machines to complex engineering projects, making these abstract concepts more relatable and easier to grasp. As we delve deeper into tension and pulley problems, you'll develop problem-solving skills that are essential for tackling more advanced physics challenges. So, let's get started on this exciting journey of discovery, where we'll unravel the mysteries of tension and pulleys together!

    FAQs

    Here are some frequently asked questions about tension and pulley problems:

    1. What is the formula for tension?

    There isn't a single formula for tension, as it depends on the specific scenario. However, in many cases, tension can be calculated using Newton's Second Law: F = ma. For a simple hanging mass, the tension would equal the weight of the object: T = mg, where m is mass and g is gravitational acceleration (9.8 m/s²).

    2. How do you calculate tension on a line?

    To calculate tension on a line, consider all forces acting on the object connected to the line. Use Newton's Second Law and resolve forces into their components. For a stationary object, the sum of forces should equal zero. For a moving object, the net force will equal mass times acceleration.

    3. How do you solve tension problems with angles?

    When solving tension problems with angles: 1. Draw a free-body diagram. 2. Resolve forces into their x and y components using trigonometry. 3. Apply Newton's Second Law for each direction. 4. Solve the resulting equations for the unknown tensions or forces.

    4. Is tension in a pulley the same throughout?

    In an ideal pulley system (assuming massless and frictionless pulleys), the tension is the same throughout the rope. However, in real-world scenarios, factors like pulley mass, friction, and rope elasticity can cause slight variations in tension.

    5. How do you calculate tension in a multiple pulley system?

    For a multiple pulley system: 1. Draw a free-body diagram for each mass and pulley. 2. Write equations for each mass using Newton's Second Law. 3. Consider the mechanical advantage of the pulley system. 4. Solve the system of equations for the unknown tensions and accelerations. Remember that the number of supporting strands reduces the effort force needed.

    Prerequisites

    Understanding tension and pulley problems in physics requires a solid foundation in fundamental concepts, particularly Newton's Second Law. This prerequisite topic is crucial for grasping the intricacies of tension and pulley systems, as it forms the basis for analyzing forces and motion in these scenarios.

    Newton's Second Law of Motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This principle is essential when dealing with tension and pulley problems because it allows us to understand how forces interact and affect the motion of objects within these systems.

    In tension and pulley problems, we often encounter situations where multiple forces act on objects connected by ropes or cables. Newton's Second Law helps us analyze these forces and determine their effects on the system's components. For instance, when solving problems involving pulleys, we need to consider the tension in the rope, the weights of objects, and any friction present in the system.

    By applying Newton's Second Law to each component of a pulley system, we can create equations that describe the motion and forces involved. This allows us to calculate important variables such as acceleration, tension, and the forces required to maintain equilibrium or produce specific motions.

    Moreover, understanding Newton's Second Law helps in visualizing how changes in one part of a pulley system can affect the entire arrangement. For example, increasing the mass of an object in a pulley system will alter the tensions and accelerations throughout the system, and Newton's Second Law provides the framework to quantify these changes.

    Students who have a strong grasp of Newton's Second Law will find it easier to approach tension and pulley problems systematically. They will be better equipped to identify the forces at play, set up the necessary equations, and solve for unknown variables. This prerequisite knowledge also aids in understanding more complex concepts related to tension and pulleys, such as mechanical advantage and efficiency in pulley systems.

    In conclusion, mastering Newton's Second Law is essential for tackling tension and pulley problems effectively. It provides the fundamental principles needed to analyze forces, predict motion, and solve a wide range of problems involving these mechanical systems. By building a strong foundation in this prerequisite topic, students will be well-prepared to delve into the fascinating world of tension and pulley physics, enabling them to solve complex problems and gain a deeper understanding of mechanical systems in the real world.