Solving two dimensional vector problems

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

Get the most by viewing this topic in your current grade. Pick your course now.

?
Intros
Lessons

  1. Introduction to solving two dimensional vector problems

    • Overview of trigonometry strategies for different types of vector problems
    • Definition of the law of sines and the law of cosines
?
Examples
Lessons
  1. Use the law of sines to solve triangles
    1. Find the length of side c
      triangle to solve for side c
    2. Find the angle &theta
      triangle to solve for angle theta
  2. Use the law of cosines to solve triangles
    1. For the following triangle:
      triangle to solve
      1. Find the length of the unknown side.
      2. Find the angle θ
    2. A paper airplane is thrown 11.0 m [W], then thrown 14.0 m, then 16.0 m. The final throw returns it to its original position. Find the angle of the 14.0 m throw.
      airplane triangle to solve
  3. Solve a vector word problem using the laws of sines and cosines

    To get to school, Pauline leaves her house and walks due east 1.40 km, then takes a shortcut by walking 0.650 km [35° S of E] through a park. Find her displacement from home to school.

    1. Solve a difficult vector triangle using geometry

      Solve the equation A⃗+B⃗=C⃗\vec{A} + \vec{B} = \vec{C} .

      vector
      Topic Notes
      ?

      In this lesson, we will learn:

      • How to solve two dimensional vector problems using the law of sines and the law of cosines

      Notes:

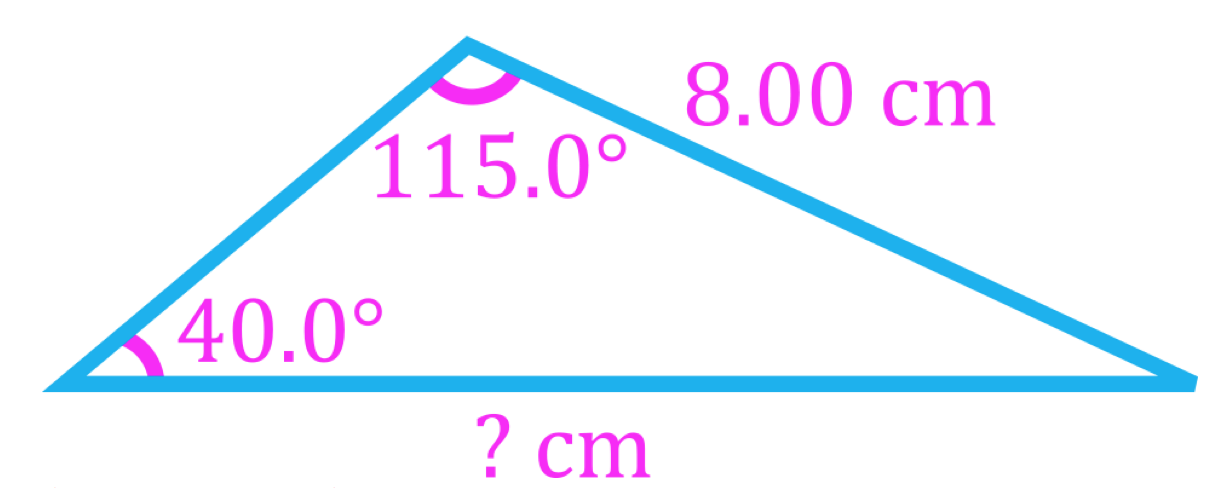
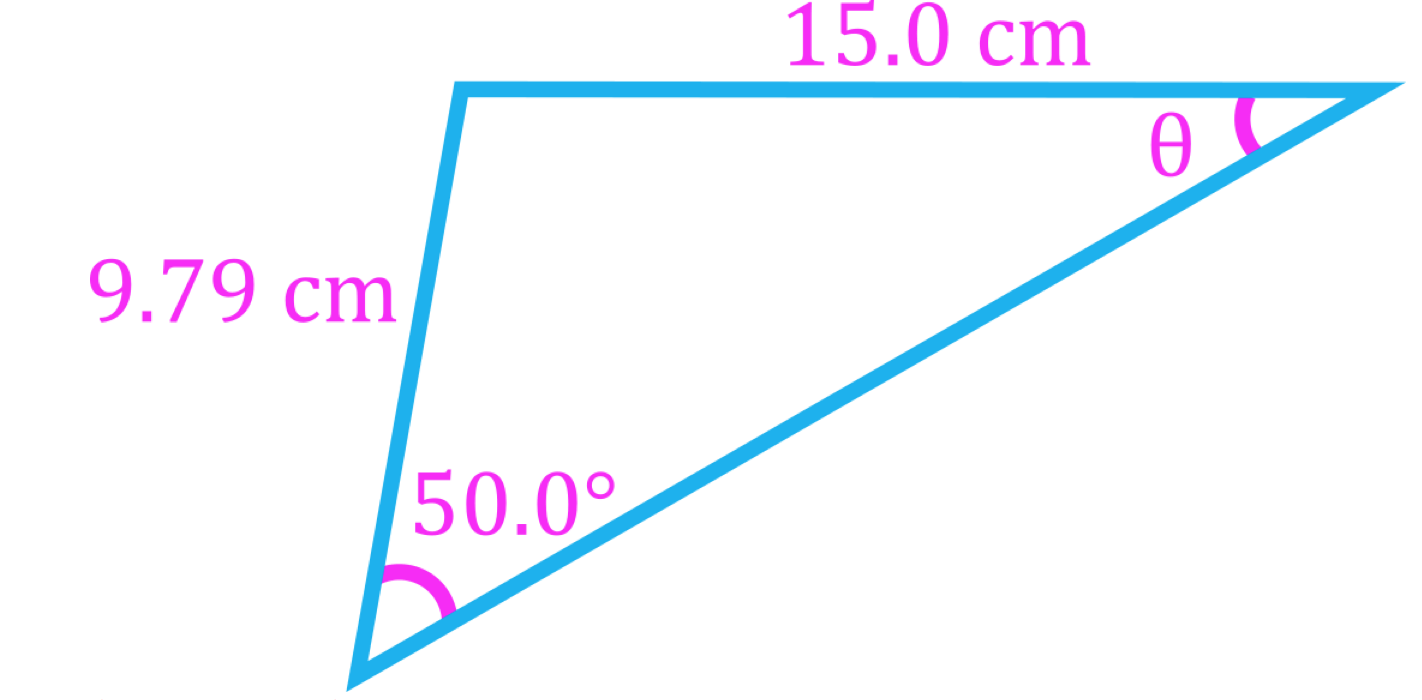
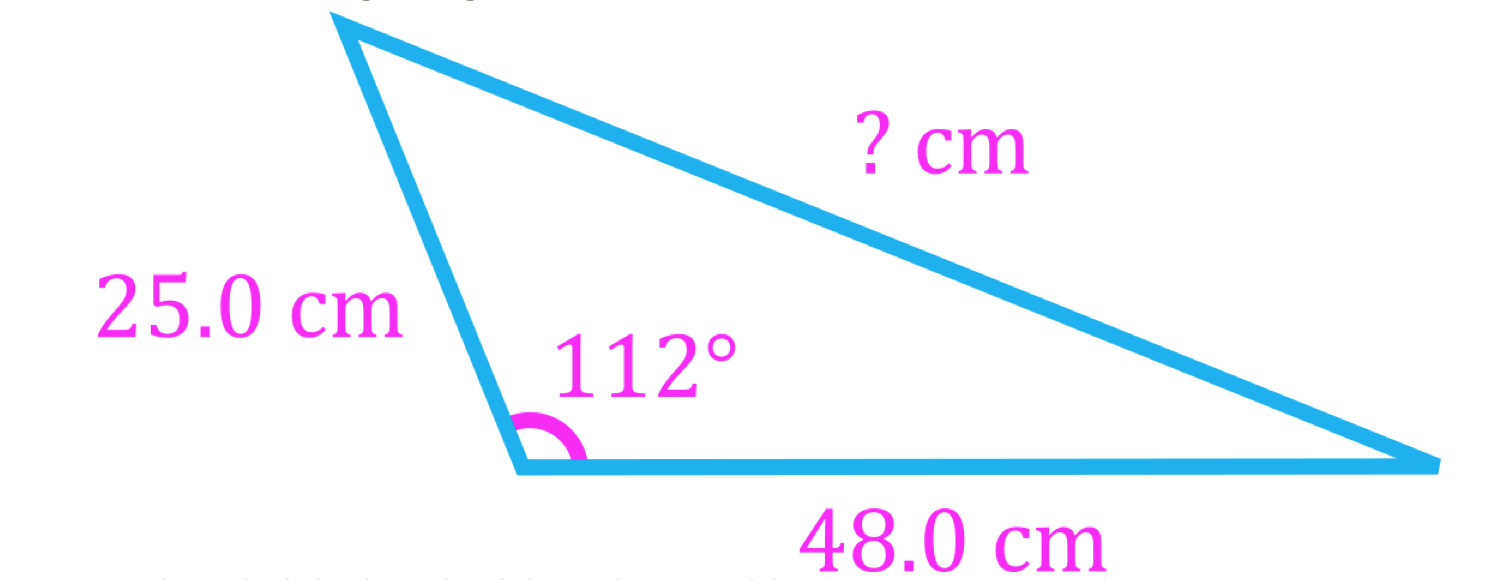
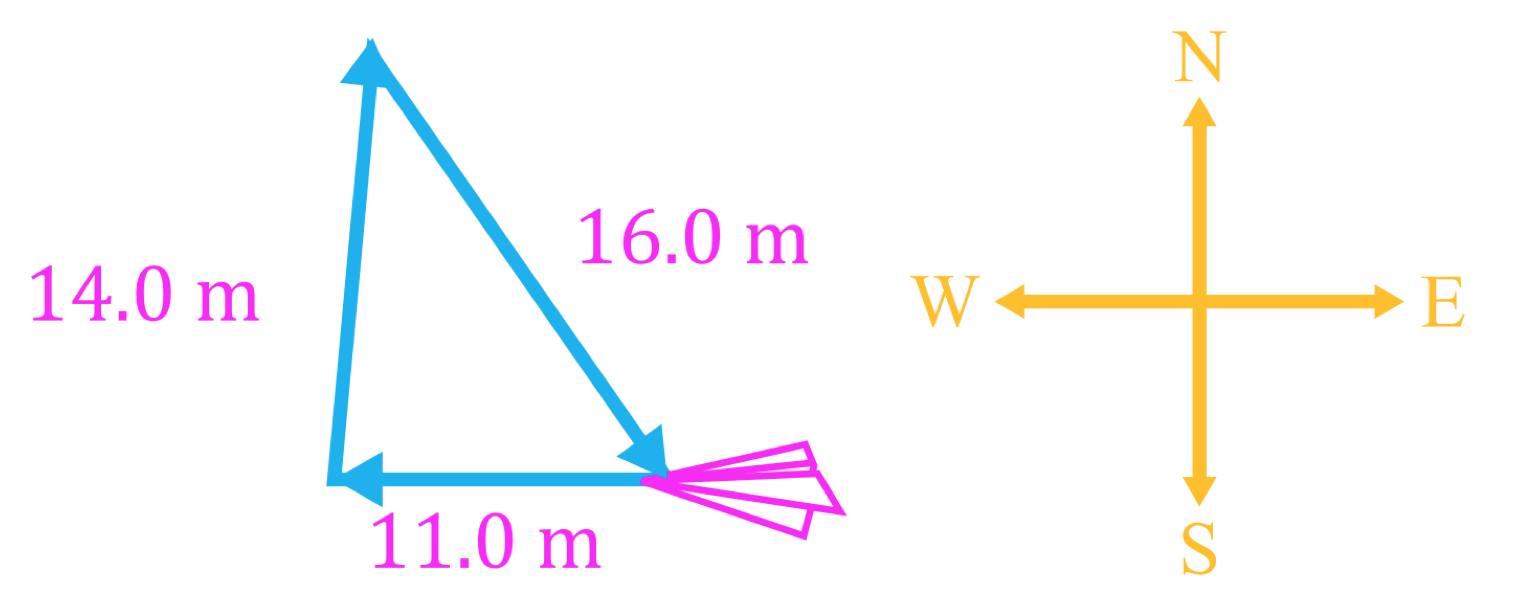
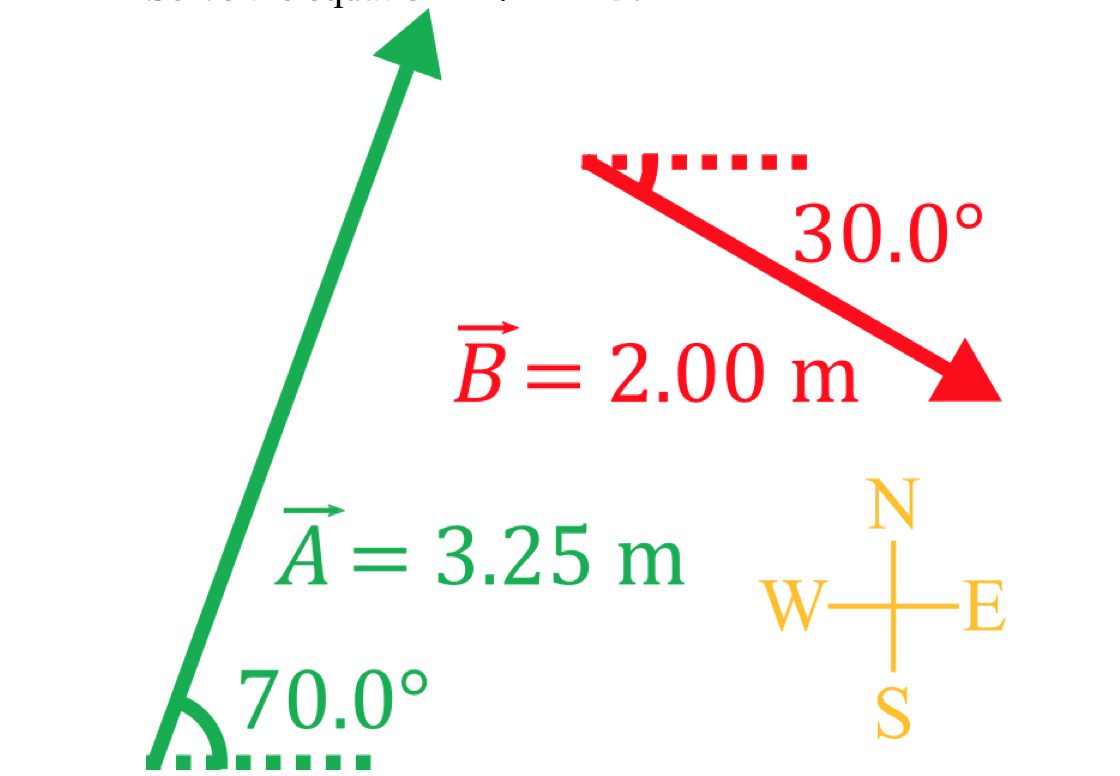
      • Often, vector equations in physics problems result in vector triangles which can be solved using trigonometry
      • At least three pieces of information are needed to solve a triangle, which can be three side lengths (SSS), two side lengths and one angle (SSA, SAS), or one side length and two angles (SAA, ASA).
        • Knowing three angles (AAA) does not let you solve a triangle since you will not be able to solve for the side lengths. There is no way to know the size of the triangle without more information.
      • You can always solve a triangle that you know four or more pieces of information about.
      • Vector triangles that do not contain right angles can be solved either by breaking vectors into their components or using the law of sines and the law of cosines, which are trigonometric laws that apply to all triangles

      Law of Sines

      asinA=bsinB=csinC\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}
      a,b,c: length of sides a,b,c
      A,B,C: angles opposite sides a, b, c

      Law of Cosines

      c2=a2+b2−2ab cosCc^2 = a^2 + b^2 - 2ab \,cosC