Rotational Vs. translational kinematics
Intros
Examples
Lessons
- A centrifuge starts from rest and has an angular acceleration of 150 rad/s2 for 2.5s.
- A car engine slows down from 4200rpm to 600rpm in 2.0s.
- A high-speed jet takes 1.5 min to turn through 20 complete revolutions before reaching its final speed.
- To move a large pottery wheel with a radius of 22.0cm, a small rubber wheel is used. Wheels are mounted and their circular edges are in contact. The radius of the small wheel is 3.0cm and it accelerates at the rate of 6.4 rad/s2 without slipping.
- A car reduces its speed uniformly from 86km/h to 44 km/h, during this time the wheels of the car with a diameter of 0.60m, make 66 revolutions.
Topic Notes
Introduction to Rotational vs. Translational Kinematics
Welcome to our exploration of rotational and translational kinematics! As your math tutor, I'm excited to guide you through this fascinating topic. Let's start with the introduction video, which provides a clear visual representation of these two types of motion. This video is crucial in understanding the fundamental differences between rotational and translational kinematics. In translational motion, an object moves along a straight line, changing its position in space. Think of a car driving down a highway. Rotational motion, on the other hand, involves an object spinning around a fixed axis, like a merry-go-round. The key difference lies in how we describe their motion: translational uses linear displacement, velocity, and acceleration, while rotational uses angular displacement, velocity, and acceleration. As we delve deeper, you'll see how these concepts are interconnected and apply to real-world scenarios. Ready to spin into action and translate this knowledge into understanding? Let's get started!
Defining Rotational Motion and Key Concepts
Understanding Rotational Motion
Rotational motion is a fundamental concept in physics that describes the circular movement of an object around a fixed point or axis. Unlike translational motion, where an object moves in a straight line, rotational motion involves spinning or revolving. This type of motion is ubiquitous in our daily lives, from the turning of a car's wheels to the rotation of the Earth around its axis.
Rigid Objects in Rotational Motion
A rigid object is a key element in understanding rotational motion. It's defined as a body whose particles maintain a fixed distance from each other during movement. In rotational motion, a rigid object rotates as a whole, with all its parts moving in circular paths around a common axis. Examples of rigid objects include a spinning top, a rotating fan blade, or a merry-go-round.
The Axis of Rotation
The axis of rotation is an imaginary line around which an object rotates. It's crucial in defining the object's rotational behavior. For instance, the Earth's axis of rotation is an imaginary line that passes through its North and South poles. Understanding the axis of rotation helps in analyzing various aspects of rotational motion, such as angular velocity and angular acceleration.
Comparing Rotational and Translational Motion
While rotational motion involves movement around an axis, translational motion refers to the movement of an object from one point to another along a straight path. Here's a quick comparison:
- Path: Rotational motion follows a circular path, while translational motion follows a straight line.
- Reference Point: Rotational motion is described relative to an axis, whereas translational motion is described relative to a fixed point in space.
- Measurement: Rotational motion is measured in angular terms (like degrees or radians), while translational motion is measured in linear terms (like meters).
Angular Displacement in Rotational Motion
Angular displacement is a key concept in rotational motion, analogous to linear displacement in translational motion. It represents the angle through which an object rotates from its initial position. Angular displacement is typically measured in radians, a unit that relates the arc length of a circle to its radius. Understanding angular displacement is crucial for analyzing the rotational behavior of objects.
Practical Examples of Rotational Motion
To better illustrate the difference between rotational and translational motion, consider these examples:
- A car moving down a straight road exhibits translational motion.
- The wheels of the same car, however, demonstrate rotational motion around their axles.
- A person walking in a straight line shows translational motion.
- A figure skater spinning on the ice displays rotational motion.
The Importance of Radians in Rotational Motion
Radians are the preferred unit for measuring angles in radians. One radian is defined as the angle subtended at the center of a circle by an arc length equal to the radius of the circle. Using radians simplifies many equations in rotational dynamics and provides a natural way to relate angular and linear quantities.
Conclusion
Understanding rotational motion, rigid objects, and the axis of rotation is essential in physics and engineering. These concepts help us analyze and predict the behavior of rotating systems, from simple machines to complex celestial bodies. By comparing rotational motion to translational motion, we gain a deeper appreciation for the diverse ways objects can move in our universe. Whether it's the spin of a planet or the rotation of a motor, these principles underlie countless phenomena in our world. For more information on this topic, you can refer to resources on measuring angles in radians.
Variables in Rotational Motion
Rotational motion is a fundamental concept in physics that describes the movement of objects around a fixed axis. To understand rotational motion fully, it's essential to grasp the key variables involved. These variables are angular displacement, angular velocity, and angular acceleration. Each of these has a counterpart in translational motion, making it easier to draw parallels and understand their significance.
Angular displacement (θ) is the angle through which an object rotates. It's measured in radians, with one complete rotation equal to 2π radians or 360 degrees. This variable is analogous to linear displacement in translational motion. For example, if a wheel rotates a quarter turn, its angular displacement would be π/2 radians or 90 degrees.
Angular velocity (ω) represents the rate of change of angular displacement with respect to time. It's measured in radians per second (rad/s). The formula for angular velocity is ω = Δθ / Δt, where Δθ is the change in angular displacement and Δt is the time interval. Angular velocity is similar to linear velocity in translational motion, but instead of measuring distance per unit time, it measures angle per unit time. For instance, if a fan blade rotates through 2π radians (one complete rotation) in 0.5 seconds, its angular velocity would be 4π rad/s.
Angular acceleration (α) is the rate of change of angular velocity with respect to time. It's measured in radians per second squared (rad/s²). The formula for angular acceleration is α = Δω / Δt, where Δω is the change in angular velocity and Δt is the time interval. This variable corresponds to linear acceleration in translational motion. An example of angular acceleration would be a spinning top slowing down due to friction, experiencing a negative angular acceleration.
To better understand these concepts, let's compare them directly to their translational counterparts:
- Angular displacement (θ) in radians Linear displacement (s) in meters
- Angular velocity (ω) in rad/s Linear velocity (v) in m/s
- Angular acceleration (α) in rad/s² Linear acceleration (a) in m/s²
It's important to note that there's a relationship between rotational and translational motion variables. For a point on a rotating object, its linear velocity (v) is related to its angular velocity (ω) by the equation v = ωr, where r is the distance from the axis of rotation. Similarly, the linear acceleration (a) is related to the angular acceleration (α) by a = αr.
These rotational motion variables play crucial roles in various applications. For example, in engineering, understanding angular velocity is essential for designing efficient turbines and motors. In sports, coaches use concepts of angular acceleration to help athletes improve their performance in activities like discus throwing or figure skating.
To further illustrate these concepts, consider a merry-go-round. As it starts to spin, it undergoes angular acceleration, increasing its angular velocity. Once it reaches a constant speed, it maintains a steady angular velocity. The total angle through which it rotates during a ride represents its angular displacement.
In conclusion, mastering the variables of rotational motion - angular displacement, angular velocity, and angular acceleration - is crucial for a comprehensive understanding of physics and its real-world applications. By drawing parallels with their translational counterparts and understanding their formulas and units, we can better analyze and predict the behavior of rotating objects in various scenarios.
Translational-Rotational Analogs
Understanding the relationship between translational and rotational motion is crucial in physics and engineering. These two types of motion share many similarities, with each translational variable having a rotational counterpart. This comparison helps in grasping the concepts of rotational kinematics and dynamics more effectively.
Comparison Table: Translational vs. Rotational Motion Variables
| Translational Motion | Rotational Motion |
|---|---|
| Distance (s) | Angular Displacement (θ) |
| Velocity (v) | Angular Velocity (ω) |
| Acceleration (a) | Angular Acceleration (α) |
| Mass (m) | Moment of Inertia (I) |
| Force (F) | Torque (τ) |
| Momentum (p) | Angular Momentum (L) |
| Kinetic Energy (KE = ½mv²) | Rotational Kinetic Energy (KE = ½Iω²) |
The significance of these comparisons lies in their ability to help us understand and solve rotational motion problems using our knowledge of translational motion. For instance, just as we use v = d/t for linear velocity, we can use ω = θ/t for angular velocity. This analogy extends to more complex relationships as well.
Let's explore some key relationships between linear and angular quantities:
- Linear Velocity and Angular Velocity: For a point on a rotating object, v = rω, where r is the distance from the axis of rotation. This relationship shows how the linear velocity of a point depends on its distance from the rotation axis and the object's angular velocity.
- Linear Acceleration and Angular Acceleration: The tangential acceleration of a point is related to angular acceleration by a = rα. Additionally, there's a centripetal acceleration component given by ac = rω².
- Force and Torque: Torque, τ = r × F, represents the rotational equivalent of force. It determines the object's angular acceleration, just as force determines linear acceleration.
To illustrate these relationships, consider a merry-go-round:
- As it rotates at a constant angular velocity (ω), a child sitting near the edge experiences a greater linear velocity than one sitting closer to the center, demonstrating v = rω.
- When the merry-go-round speeds up, the angular acceleration (α) is the same for all points, but the tangential acceleration (a = rα) is greater for points farther from the center.
- The force needed to push the merry-go-round (creating torque) depends on where you push - pushing near the edge (larger r) requires less force than pushing near the center for the same torque.
Understanding these analogies and relationships is crucial in various applications, from engineering rotating machinery to analyzing celestial body motions. For instance, in designing a centrifuge, engineers must consider both the angular velocity and the radius to determine the effective g-force experienced by the samples.
In conclusion, the parallels between translational and rotational motion provide a powerful framework for understanding complex rotational systems. By recognizing these analogies, students and professionals can more easily transition from linear to rotational problem-solving, applying familiar concepts in new contexts. This comparative approach not
Relating Linear and Angular Motion
Understanding the relationships between linear and angular quantities is crucial in comprehending rotational motion. These relationships provide a bridge between the familiar concepts of linear motion and the more complex realm of rotational dynamics. Two key equations that encapsulate these relationships are v = rω and a = rα, where v represents linear velocity, ω is angular velocity, a denotes linear acceleration, α is angular acceleration, and r is the radius of rotation.
Let's first explore the equation v = rω. This formula relates linear velocity to angular velocity. In rotational motion, different points on a rotating object move with different linear velocities, but they all share the same angular velocity. The linear velocity of a point depends on its distance from the axis of rotation. The farther a point is from the axis, the greater its linear velocity. This relationship is captured by v = rω, where r is the radial distance from the axis of rotation.
To derive this equation, consider a point on a rotating object. As the object completes one full rotation, this point traces out a circle. The circumference of this circle is 2πr. In one revolution, the point travels this distance in a time T, where T is the period of rotation. Therefore, the linear velocity is v = 2πr / T. Since angular velocity ω is defined as 2π / T, we can substitute this into our equation to get v = rω.
The equation a = rα follows a similar logic but for acceleration. Just as linear velocity is related to angular velocity, linear acceleration is related to angular acceleration. This equation tells us that the linear acceleration of a point on a rotating object is proportional to its distance from the axis of rotation and the angular acceleration of the object.
To derive a = rα, we start with the equation v = rω and differentiate both sides with respect to time. The derivative of v with respect to time is a (linear acceleration), and the derivative of ω with respect to time is α (angular acceleration). Assuming r is constant, we get a = rα.
These relationships are invaluable in solving rotational motion problems. They allow us to convert between linear and angular quantities, making it possible to apply our knowledge of linear motion to rotational scenarios. For example, if we know the angular velocity of a wheel and its radius, we can easily calculate the linear velocity of a point on its rim using v = rω.
Consider a practical example: a car wheel with a radius of 0.3 meters rotating at 10 radians per second. Using v = rω, we can calculate that a point on the rim of the wheel has a linear velocity of 3 m/s (0.3 m × 10 rad/s). If the wheel then accelerates at an angular rate of 2 rad/s², we can use a = rα to find that a point on the rim experiences a linear acceleration of 0.6 m/s² (0.3 m × 2 rad/s²).
These relationships also help us understand phenomena like why the outer edge of a merry-go-round moves faster than the inner parts, or why a figure skater spins faster when they pull their arms in close to their body. In the case of the merry-go-round, all points rotate with the same angular velocity, but points farther from the center have a greater linear velocity due to the v = rω relationship.
In conclusion, the equations v = rω and a = rα are fundamental to understanding rotational motion. They provide a crucial link between linear and angular quantities, allowing us to apply our intuition about linear motion to rotational scenarios. By mastering these relationships, we can solve a wide range of rotational motion problems and gain deeper insights into the behavior of rotating objects in the world around us.
Tangential and Centripetal Acceleration
In the realm of rotational motion, two key concepts play a crucial role in understanding the dynamics of objects moving in circular motion dynamics: tangential acceleration and centripetal acceleration. These concepts are fundamental to comprehending the behavior of rotating bodies and their relationship to linear and angular motion.
Tangential acceleration is the component of acceleration that acts along the tangent to the circular path. It is responsible for changes in the speed of the rotating object. When an object experiences tangential acceleration, its linear velocity changes in magnitude but not in direction. The formula for tangential acceleration is:
at = α * r
Where at is tangential acceleration, α is angular acceleration, and r is the radius of the circular path. This formula illustrates the direct relationship between tangential and angular acceleration, highlighting how changes in rotational speed affect the object's linear velocity.
On the other hand, centripetal acceleration is the component of acceleration directed towards the center of the circular path. It is responsible for maintaining the circular motion by constantly changing the direction of the object's velocity vector. The formula for centripetal acceleration is:
ac = v2 / r = ω2 * r
Where ac is centripetal acceleration, v is linear velocity, ω is angular velocity, and r is the radius. This formula demonstrates that centripetal acceleration depends on both the speed of rotation and the size of the circular path.
The significance of these accelerations lies in their ability to describe the complete motion of an object in circular motion dynamics. While tangential acceleration changes the object's speed, centripetal acceleration keeps it moving in a circular path. Together, they provide a comprehensive understanding of the object's behavior.
To illustrate these concepts, consider a car driving around a circular track. As the driver accelerates, the car experiences tangential acceleration, increasing its speed along the track. Simultaneously, the car must constantly turn to stay on the circular path, which is the result of centripetal acceleration. Without centripetal acceleration, the car would continue in a straight line tangent to the circle.
The relationship between linear and angular quantities in circular motion is crucial for understanding these accelerations. Linear velocity (v) is related to angular velocity (ω) by the equation v = ω * r. Similarly, linear acceleration (a) is related to angular acceleration (α) by a = α * r. These relationships allow us to convert between linear and angular measurements, providing a comprehensive view of rotational motion.
In practical applications, understanding tangential and centripetal acceleration is essential in various fields. Engineers designing roller coasters must consider both accelerations to ensure thrilling yet safe rides. Physicists studying planetary motion use these concepts to analyze orbital dynamics. Even in everyday scenarios, like a car navigating a curved road, these principles are at play.
It's important to note that while tangential and centripetal accelerations are perpendicular to each other, they can occur simultaneously. The total acceleration of an object in circular motion is the vector sum of these two components. This total acceleration can be visualized as a changing vector that points inward and forward as the object moves around its circular path.
In conclusion, tangential and centripetal accelerations are fundamental concepts in rotational motion. They provide a comprehensive framework for understanding how objects move in circular paths, relating linear and angular motion, and explaining the forces involved in maintaining circular trajectories. By mastering these concepts, one gains deep insights into the dynamics of rotating systems, from the microscopic world of atomic particles to the vast scales of celestial mechanics.
Rotational Kinematics Equations
Rotational kinematics equations are fundamental in understanding and analyzing the motion of rotating objects. These equations bear striking similarities to their translational counterparts, making them easier to grasp for those familiar with linear motion. In this section, we'll explore the key rotational motion equations, their applications, and how they relate to translational kinematics equations.
The primary variables in rotational kinematics are angular displacement (θ), angular velocity (ω), and angular acceleration (α). These correspond to displacement (x), velocity (v), and acceleration (a) in translational motion. The rotational kinematics equations are:
- ω = ω + αt
- θ = θ + ωt + ½αt²
- ω² = ω² + 2α(θ - θ)
- θ = θ + ½(ω + ω)t
These equations mirror the translational kinematics equations, with angular quantities replacing linear ones. For instance, equation 1 is analogous to v = v + at in linear motion. This parallel structure allows for easier comprehension and application of rotational concepts.
To solve rotational motion problems, we apply these equations similarly to how we use translational equations. For example, consider a spinning wheel that starts from rest and reaches an angular velocity of 10 rad/s in 5 seconds. Using equation 1, we can calculate the angular acceleration: α = (ω - ω) / t = (10 - 0) / 5 = 2 rad/s². Once we know the angular acceleration, we can use equation 2 to find the angular displacement during this time.
Another common scenario involves calculating the final angular velocity of an object given its initial velocity, angular displacement, and angular acceleration. In this case, equation 3 proves most useful. For instance, if a turntable starts at 33 rpm, rotates through 10 revolutions while slowing down, and we know its angular acceleration, we can determine its final angular velocity.
It's crucial to pay attention to units when working with rotational kinematics. Angular displacement is typically measured in radians, angular velocity in radians per second (rad/s), and angular acceleration in radians per second squared (rad/s²). However, you may encounter other units, necessitating conversions. A common conversion is from revolutions per minute (rpm) to radians per second. To convert, use the formula: ω (rad/s) = (rpm × 2π) / 60. For example, 120 rpm is equivalent to (120 × 2π) / 60 = 4π 12.57 rad/s.
Applying these equations to real-world scenarios helps solidify understanding. Consider a ceiling fan that accelerates from rest to 300 rpm in 10 seconds. First, convert 300 rpm to rad/s: (300 × 2π) / 60 = 10π rad/s. Then, use equation 1 to find the angular acceleration: α = (10π - 0) / 10 = π rad/s². With this information, you can calculate the total angular displacement using equation 2.
Another practical application is in automotive engineering. When a car's engine revs up from 1000 rpm to 5000 rpm in 3 seconds, you can calculate its angular acceleration. First, convert both speeds to rad/s, then apply equation 1 to find α. This information is crucial for designing efficient engines and transmissions.
In conclusion, rotational kinematics equations are powerful tools for analyzing rotating objects. Their similarity to translational kinematics equations makes them accessible, while their applications span various fields from engineering to physics. By understanding these equations and practicing their application, you'll be well-equipped to tackle complex rotational motion problems across diverse scenarios.
Rolling Without Slipping
Rolling without slipping is a fundamental concept in physics that combines both rotational and translational motion. This phenomenon occurs when an object, typically circular in shape, moves along a surface while rotating in such a way that there is no relative motion between the point of contact and the surface. Understanding rolling without slipping is crucial for analyzing the motion of wheels, gears, and various other mechanical systems.
The key condition for rolling without slipping is the presence of static friction between the rolling object and the surface. Static friction prevents the object from sliding or skidding, ensuring that the point of contact remains stationary relative to the surface at any given instant. This friction force is responsible for converting some of the object's translational energy into rotational energy, and vice versa.
In rolling without slipping, the object's motion can be described by two components: translational motion of its center of mass and rotational motion about its axis. The translational velocity of the center of mass (v) is related to the angular velocity (ω) and the radius of the object (r) by the equation: v = ωr. This relationship is fundamental to solving problems involving rolling motion.
The total kinetic energy of a rolling object consists of both translational kinetic energy and rotational kinetic energy. The translational kinetic energy is given by (1/2)mv², where m is the mass of the object and v is its velocity. The rotational kinetic energy is expressed as (1/2)Iω², where I is the moment of inertia and ω is the angular velocity. Understanding the distribution of energy between these two forms is essential for analyzing rolling motion problems.
Real-world examples of rolling without slipping are abundant. Car wheels rolling on a road, a bowling ball moving down a lane, or a cylinder rolling down an inclined plane all demonstrate this principle. In each case, the interaction between the object and the surface, mediated by static friction, allows for efficient transfer of energy and smooth motion.
When solving problems involving rolling without slipping, it's important to consider both the linear and angular aspects of the motion. Key equations include the relationship between linear and angular velocity (v = ωr), the rolling condition (distance traveled = angle rotated × radius), and energy conservation principles. Additionally, the role of static friction in providing the necessary torque for rotation must be taken into account.
One common problem type involves an object rolling down an inclined plane. In this scenario, gravitational potential energy is converted into both translational and rotational kinetic energy. The distribution of energy depends on the object's moment of inertia, which varies based on its shape and mass distribution. For instance, a solid sphere and a hollow sphere of the same mass and radius will roll down an incline at different rates due to their different moments of inertia.
Another important consideration in rolling without slipping is the concept of instantaneous axis of rotation. For a rolling object, this axis is located at the point of contact with the surface. Understanding this helps in visualizing the motion and applying the principles of rotational dynamics correctly.
The study of rolling without slipping extends beyond simple circular objects. It applies to more complex shapes and systems, such as gears in machinery or the motion of a bicycle. In these cases, the principles of rolling motion are combined with other mechanical concepts to analyze and optimize performance.
In conclusion, rolling without slipping is a fascinating application of physics that bridges translational and rotational motion. Its understanding is crucial for engineers, physicists, and anyone interested in the mechanics of motion. By mastering this concept, one gains insight into a wide range of phenomena, from the simple rolling of a ball to the complex workings of mechanical systems. The interplay between static friction, translational kinetic energy, and rotational kinetic energy in rolling motion provides a rich field for study and practical application in numerous real-world scenarios.
Conclusion
In this article, we explored the intricate relationship between rotational and translational motion, two fundamental concepts in physics. We learned that while translational motion involves the movement of an object's center of mass, rotational motion describes the object's spinning around an axis. Understanding the interplay between these two types of motion is crucial for solving complex physics problems. We discussed key concepts such as angular velocity, moment of inertia, and torque, which are essential for analyzing rotational motion. The article emphasized how these principles apply to real-world scenarios, from the motion of planets to the mechanics of machinery. The introduction video provided a visual foundation for grasping these concepts, making them more accessible to learners. As we've seen, mastering the relationship between rotational and translational motion opens up a deeper understanding of the physical world around us. We encourage readers to further explore this fascinating topic, as it forms the basis for many advanced physics concepts and applications in engineering and technology.
Rotational Motion
In this section, we will explore the concept of rotational motion, which is a fundamental aspect of rotational kinematics. Understanding rotational motion involves several key concepts and definitions that are crucial for grasping the overall topic.
Step 1: Understanding Rotational Motion
Rotational motion refers to the movement of an object around a central axis. To fully comprehend rotational motion, it is essential to understand the definitions of a rigid object and the axis of rotation. A rigid object is one that maintains a definite shape, with its particles fixed in position relative to each other. This means that the particles do not move relative to one another, ensuring the object retains its shape during motion.
Step 2: Defining a Rigid Object
A rigid object is an object with a definite shape, where the particles composing the object are at fixed positions and do not move relative to one another. For example, if you hold a piece of paper and move it up and down, the particles (or your fingers holding the paper) move relative to each other, indicating it is not a rigid object. In contrast, if you hold a solid object like a mouse and move it, the particles (or your fingers) do not move relative to each other, indicating it is a rigid object.
Step 3: Axis of Rotation
The axis of rotation is a crucial concept in rotational motion. It is the line around which all points of a rigid object move in a circle. The center of all these circles lies on the axis of rotation, which is perpendicular to the plane of motion. For instance, if you consider a rigid disc, all points on the disc rotate around the center, and the line passing through the center of all these circles is the axis of rotation.
Step 4: Translational-Rotational Analogs
In rotational motion, we use variables analogous to those in translational motion. In translational motion, we talk about distance, speed, and acceleration. Similarly, in rotational motion, we discuss angular displacement, angular velocity, and angular acceleration. These variables help us formulate equations and solve problems related to rotational motion.
Step 5: Angular Displacement
Angular displacement refers to the change in the angle through which an object rotates. Instead of moving through different positions (as in translational motion), an object in rotational motion moves through different angles. We denote the initial angle as θi and the final angle as θf. The change in angle, or angular displacement, is given by θf - θi and is measured in radians.
Step 6: Angular Velocity
Angular velocity is the rate of change of angular displacement over time. It is analogous to velocity in translational motion. We denote angular velocity by the Greek letter ω (omega). Mathematically, it is expressed as ω = Δθ / Δt, where Δθ is the change in angle and Δt is the time taken. The unit of angular velocity is radians per second.
Step 7: Angular Acceleration
Angular acceleration is the rate of change of angular velocity over time. It is analogous to acceleration in translational motion. We denote angular acceleration by the Greek letter α (alpha). Mathematically, it is expressed as α = Δω / Δt, where Δω is the change in angular velocity and Δt is the time taken. The unit of angular acceleration is radians per second squared.
Step 8: Tangential and Centripetal Acceleration
In rotational motion, we also need to consider tangential and centripetal acceleration. Tangential acceleration refers to the acceleration along the edge of the rotating object, while centripetal acceleration points towards the center of the rotation. These accelerations are crucial for understanding the dynamics of rotating objects.
Step 9: Rotational Kinematics Equations
Similar to translational motion, rotational motion has its own set of kinematic equations. These equations relate angular displacement, angular velocity, angular acceleration, and time. They are essential for solving problems involving rotational motion and understanding the behavior of rotating objects.
Step 10: Rolling Without Slipping
Rolling without slipping is an important concept in rotational motion. It occurs when an object rolls on a surface without sliding. In this case, the point of contact between the object and the surface is momentarily at rest. This concept is crucial for understanding the motion of wheels, gears, and other rotating objects in practical applications.
FAQs
Here are some frequently asked questions about rotational and translational motion:
-
What is the difference between rotational and translational motion?
Translational motion involves an object moving from one point to another along a straight or curved path. Rotational motion, on the other hand, involves an object spinning around a fixed axis. In translational motion, all parts of the object move in the same direction at the same speed, while in rotational motion, different parts of the object move at different speeds and in different directions.
-
What is an example of translational motion?
A car driving down a straight road is a good example of translational motion. Other examples include a ball rolling across a table, an elevator moving up or down, or a person walking in a straight line.
-
What is the analogy between translational and rotational motion?
There are several analogies between translational and rotational motion. For instance, linear displacement is analogous to angular displacement, linear velocity to angular velocity, and linear acceleration to angular acceleration. Similarly, mass in translational motion is analogous to moment of inertia in rotational motion, and force is analogous to torque.
-
How do you find translational motion?
Translational motion can be described using kinematic equations. The basic equations involve displacement (s), initial velocity (u), final velocity (v), acceleration (a), and time (t). For example, v = u + at describes how velocity changes with constant acceleration, and s = ut + ½at² describes displacement under constant acceleration.
-
What is the relationship between angular acceleration and translational acceleration?
For a rotating object, the relationship between angular acceleration (α) and translational acceleration (a) of a point on the object is given by a = rα, where r is the distance of the point from the axis of rotation. This equation shows that points farther from the axis of rotation experience greater translational acceleration for the same angular acceleration.
Prerequisite Topics
Understanding rotational vs. translational kinematics is crucial in physics, but to fully grasp this concept, it's essential to have a solid foundation in several prerequisite topics. These fundamental areas provide the necessary context and principles that underpin the complexities of rotational and translational motion.
One key prerequisite is friction: static and kinetic. This topic is vital because friction plays a significant role in both rotational and translational motion. Static friction, in particular, is crucial in understanding why objects start to move or rotate. For instance, when a wheel begins to turn, it's the static friction between the wheel and the ground that initiates the rotational motion. Without this knowledge, it's challenging to comprehend the nuances of how objects transition from rest to motion in both rotational and translational contexts.
Another critical prerequisite is rotational kinetic energy and angular momentum. This topic is directly related to rotational kinematics and provides the foundation for understanding how energy and momentum are conserved in rotating systems. Rotational kinetic energy, in particular, is essential for comparing the energy of rotating objects to those in translational motion. This comparison is at the heart of understanding the differences and similarities between rotational and translational kinematics.
While it might seem less directly related, knowledge of electric potential and electric potential energy is also valuable. Although this topic primarily deals with electrical concepts, the principles of potential energy are analogous to those in mechanical systems. Understanding gravitational potential energy, which is closely related to electric potential energy, is crucial for analyzing the energy transformations in both rotational and translational motion. This knowledge helps in comprehending how potential energy converts to kinetic energy in various motion scenarios.
By mastering these prerequisite topics, students can develop a more comprehensive understanding of rotational vs. translational kinematics. The concepts of friction provide insight into the forces that initiate and resist motion. Rotational kinetic energy and angular momentum offer a framework for analyzing rotating systems, which can then be compared and contrasted with translational motion. Finally, the principles of potential energy, whether gravitational or electric, help in understanding the energy transformations that occur in both types of motion.
In conclusion, these prerequisite topics form the building blocks for a deeper comprehension of rotational vs. translational kinematics. They provide the necessary background to analyze complex motion scenarios, compare different types of motion, and understand the underlying principles that govern both rotational and translational movement. By investing time in these foundational concepts, students will be better equipped to tackle the more advanced aspects of kinematics and mechanics in their physics studies.
In this lesson, we will learn:
- Definition of Rotational Motion, Rigid Object and The Axis of Rotation.
- Translational-Rotational Analogues
- Tangential Acceleration Vs. Centripetal Acceleration
- Rotational Kinematics Equations
- Rolling Without Slipping Motion
Notes:
Rotational Motion
- To explain the rotational motion, we need to consider a rigid object.
- A rigid object: it is an object with a definite shape, the particles composing the object are at a fixed position relative to one another.
- When an object rotates, all the points composing the object move in a circle.
- Axis of Rotation: The center of all circles lie on a line called Axis of Rotation, which is perpendicular to the page.
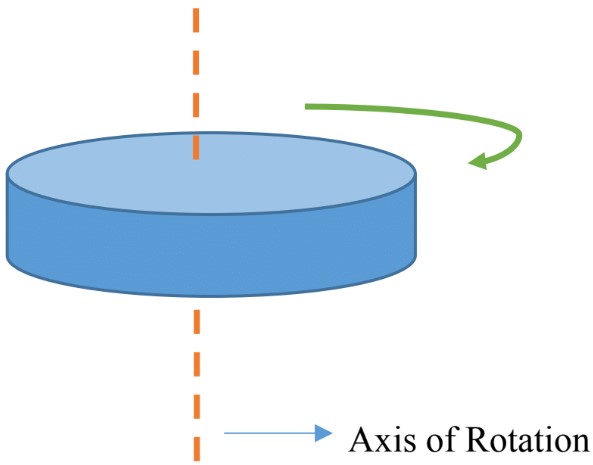
- Through rotation, the object changes position and moves through different angles;
- Similar to translational motion velocity is defined as a change in position over time elapsed;
- Similarly, the acceleration is defined as a change in velocity over time elapsed;
: Change in position, angular displacement (radians)
: Final position
: Initial position
Translational-Rotational Analogues
- Each point of a rotating object has a linear velocity and a linear acceleration, so we have to relate the linear quantities to the angular quantitates.
Tangential Acceleration Vs. Centripetal Acceleration
In rotational motion, we have to consider the two components of acceleration,
; tangential component, that changes the magnitude of the velocity and it is tangent to the direction of motion;
; centripetal competent, that changes the direction of velocity and is directed towards the center (caused by centripetal force);
To find the total acceleration we can find the magnitude of the acceleration using the Pythagoras theorem;
Rotational Kinematics Equations
The following table compares the rotational kinematics equation to the translational kinematics equation.
Conversion Factor
It is very common in rotational motion to measure the angular velocity in round per minutes (rmp), in order to convert to the standard unit of radians per second (rad/s), we use the following the conversion factor;
Rolling Without Slipping
There are many examples in everyday life, where the object rolls but it does not slip.
Examples: rolling ball, rolling wheel.
Rolling without slipping depends on the static friction between the rolling object and the floor.
In this case, we have to consider both rotational and translational motion. To relate these two types of motion, use (where is the radius).
As the following diagram represents, the wheel is rolling (Rotational Motion) to the right and at the same time, the center of gravity is changing position (Translational Motion).
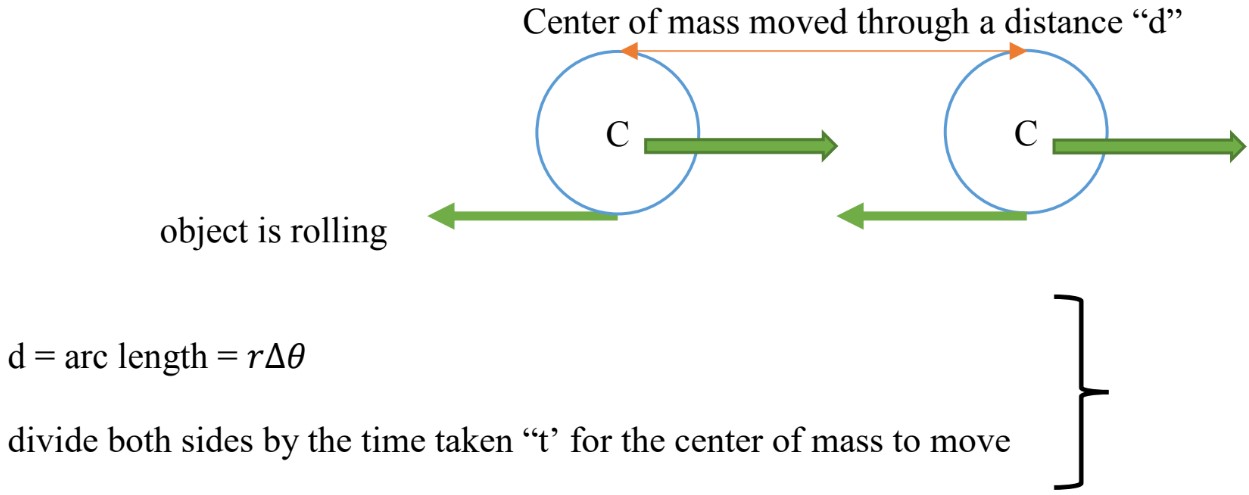
: Center of mass speed
: Radius
: Angular speed about the center of mass