Sign In
Sign Up
flag-us

Understanding Electrical Resistance: From Basics to Advanced Applications
Dive into the world of electrical resistance. Master key concepts, calculations, and real-world applications. Boost your understanding of circuits and power systems with our comprehensive guide.

Now Playing:Resistance – Example 0a
Intros
  1. Introduction to resistors and resistance:
  2. Introduction to resistors and resistance:
    Another review on circuits so far.
  3. Introduction to resistors and resistance:
    What is resistance?
Examples
  1. Solving Resistance for Resistors in Series
    Find the total resistance of the circuit.

    Introduction to Waves
    Voltage
    Jump to:NotesConceptFAQsPrerequisites
    Notes

    In this lesson, we will learn:

    • A review on what is an electric circuit and the main components: battery (voltage), closed wire path (current), and devices/resistors that use up electricity (resistance).
    • What is resistance?
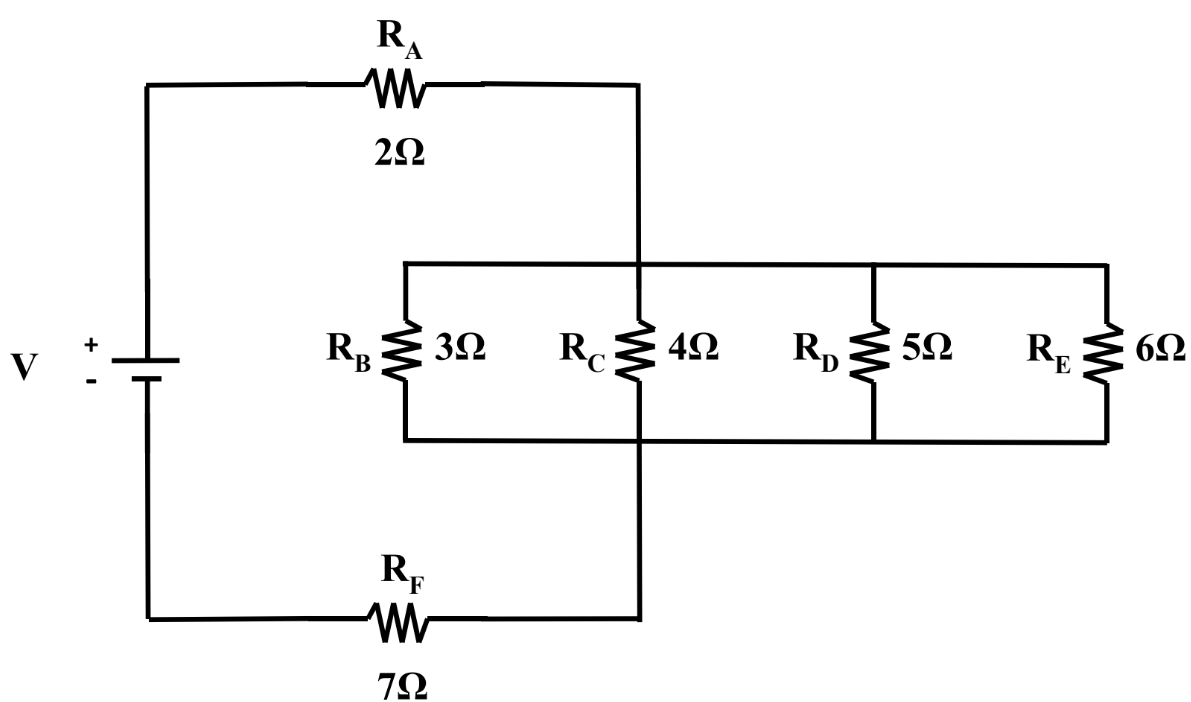
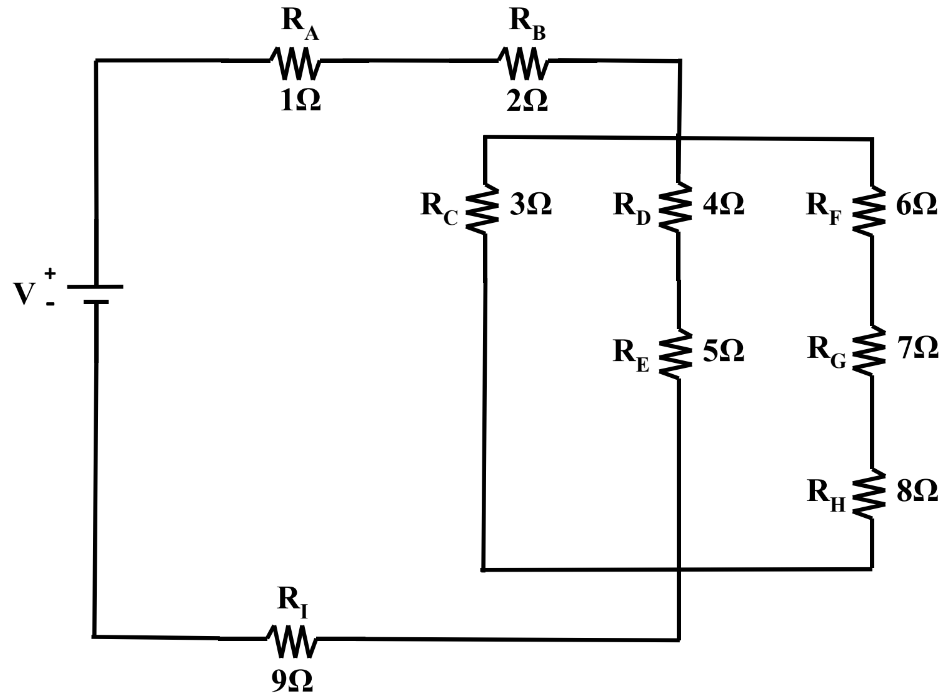
    • What is the difference between connecting your circuit in series vs. parallel configurations for resistors?
    • What is a battery and how does it provide voltage for an electric circuit?
    • How to solve resistance problems for both series and parallel circuits by using the summation equations for equivalent resistance in series and equivalent resistance in parallel
      • Req(series)=R1+R2+R3+...+Rn=∑k=1nRk R_{eq(series)} = R_{1} + R_{2} + R_{3} + . . . + R_{n} = \sum_{k=1}^{n} R_{k}

      • 1Req(parallel)=1R1+1R2+1R3+...+1Rn=Rn=∑k=1nRk \frac{1} {R_{eq(parallel)}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + ... + \frac{1}{R_{n}} = R_{n} = \sum_{k=1}^{n} R_{k}
        • OR: Req(parallel)=11R1+1R2+1R3+...1Rn=1∑k=1n1Rk R_{eq(parallel)} = \frac{1} { \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + ... \frac{1}{R_{n}} } = \frac{1} { \sum_{k=1}^{n} \frac{1}{R_{k}} }

    Notes:

    • Resistance is a property of the electronic device (resistor; or even battery and wires can have some resistance too and use up some voltage)
      • It is a measure of how difficult it is for charges to travel through the circuit
      • Resistors in a circuit represent electronic devices that use up voltage
      • The greater the resistance, the bigger the voltage drop
      • Resistances of metals are CONSTANT and INDEPENDENT of voltage
    • The unit for resistance is the ohm (Ω\Omega ) and can be determined for a circuit by dividing the voltage by the current (in preview of Ohm’s law: V=IRV=IR).
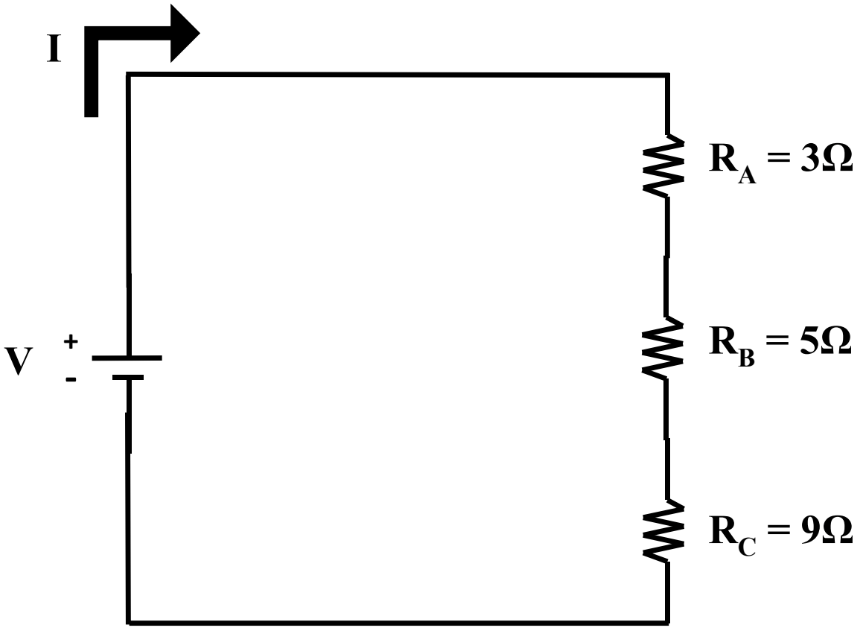
    • When solving for resistance in series, we must use the summation equation:
      • Req(series)=R1+R2+R3+...+Rn=∑k=1nRk R_{eq(series)} = R_{1} + R_{2} + R_{3} + . . . + R_{n} = \sum_{k=1}^{n} R_{k}
      • Where all resistors in series are added up for the total resistance
      • Thus, Req(series) is greater than any single RK independently; adding more resistors in series will increase the total resistance

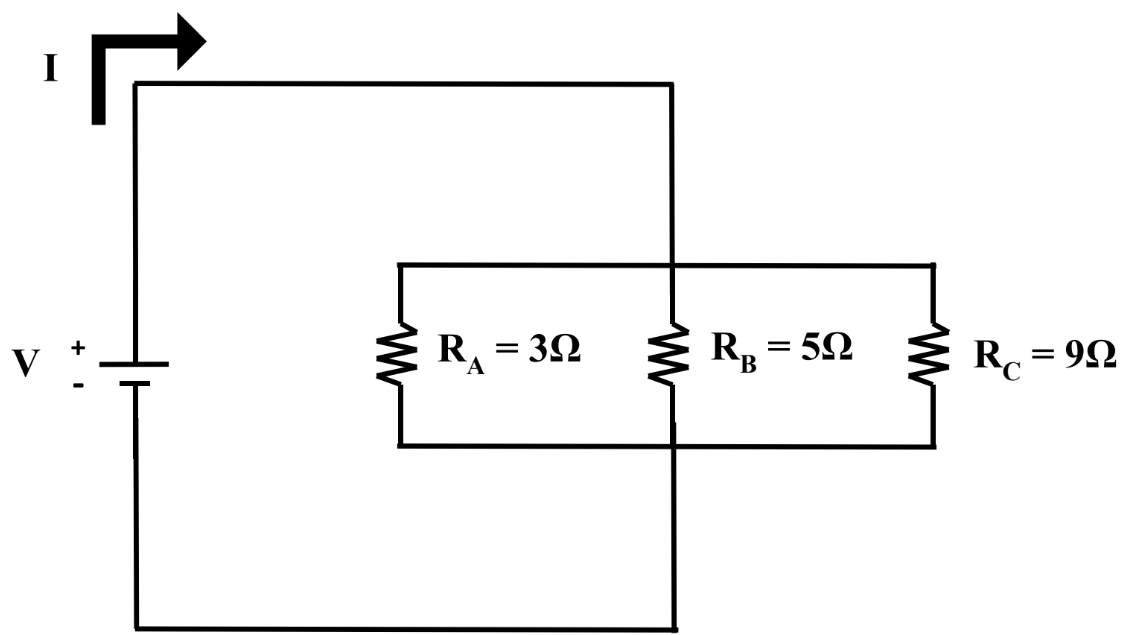
    • When solving for resistance in parallel, we must use the summation equation:
      • 1Req(parallel)=1R1+1R2+1R3+...+1Rn=Rn=∑k=1nRk \frac{1} {R_{eq(parallel)}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + ... + \frac{1}{R_{n}} = R_{n} = \sum_{k=1}^{n} R_{k}
        • OR: Req(parallel)=11R1+1R2+1R3+...1Rn=1∑k=1n1Rk R_{eq(parallel)} = \frac{1} { \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + ... \frac{1}{R_{n}} } = \frac{1} { \sum_{k=1}^{n} \frac{1}{R_{k}} }
      • Where the total resistance is equal to the inverse of the sum of all inverses of resistors (branches) in parallel
      • Thus, Req(parallel) is less than any single RK independently; adding more resistors in parallel will decrease the total resistance

    • In terms of resistance, the advantage of a series configuration is that the battery will last longer; the greater the resistance, the more difficult it is for the charges to travel; thus, less charge is drawn out of the battery over time (less current)
      • A parallel configuration generates lesser resistance, allowing charges to flow freely; thus, more charge is drawn out of the battery over time (more current)
    Concept

    Introduction to Electrical Resistance

    Welcome to our lesson on electrical resistance, a fundamental concept in understanding how circuit components interact. As introduced in our video, resistance plays a crucial role in controlling the flow of electric current. This lesson will delve into the basics of resistance, exploring its measurement and significance in electrical circuits. We'll examine how resistance affects the behavior of electrons in conductors and how it relates to other electrical properties. Understanding resistance is key to grasping Ohm's law, which forms the foundation of electrical circuit analysis. Throughout this lesson, we'll explore various materials and their resistive properties, learning how to calculate and manipulate resistance in practical applications. By the end, you'll have a solid grasp of how resistance shapes the functionality of electrical systems, from simple household appliances to complex electronic devices.

    FAQs

    1. What is electrical resistance?

      Electrical resistance is the opposition that a material or component presents to the flow of electric current. It's measured in ohms (Ω) and is fundamental to understanding how electrical circuits work. Resistance affects the amount of current that flows through a circuit for a given voltage.

    2. How do resistors in series and parallel circuits differ?

      In series circuits, resistors are connected end-to-end, and the total resistance is the sum of individual resistances. Current is the same through each resistor, but voltage drops across them. In parallel circuits, resistors are connected across the same voltage points. The total resistance is less than the smallest individual resistance, and current divides among the branches while voltage remains constant across all resistors.

    3. What is Ohm's Law and how is it used to calculate resistance?

      Ohm's Law states that voltage (V) equals current (I) multiplied by resistance (R): V = IR. To calculate resistance, you can rearrange this equation to R = V / I. This means if you know the voltage across a component and the current flowing through it, you can determine its resistance.

    4. Why is understanding resistance important in electrical engineering?

      Understanding resistance is crucial for designing and analyzing electrical circuits. It helps in controlling current flow, dividing voltage, protecting sensitive components, and managing power dissipation. Knowledge of resistance is essential for everything from simple household wiring to complex electronic devices and power systems.

    5. How does temperature affect electrical resistance?

      Temperature generally affects electrical resistance. For most metals, resistance increases with temperature due to increased atomic vibrations that impede electron flow. However, some materials like semiconductors may exhibit decreased resistance with increased temperature. This relationship is important in various applications, including temperature sensors and superconductors.

    Prerequisites

    Understanding the concept of resistance in electrical circuits is fundamental to many areas of physics and engineering. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a solid foundation in basic physics and mathematics can greatly enhance your comprehension of resistance. These foundational skills provide the necessary context and tools to fully grasp the principles of electrical resistance.

    Resistance is a key concept in electrical engineering and physics, describing how a material opposes the flow of electric current. To fully appreciate its significance, students should have a basic understanding of electricity and electric circuits. This knowledge forms the backdrop against which resistance can be explored in greater depth.

    Although not explicitly listed as prerequisites, familiarity with concepts such as voltage, current, and Ohm's law can significantly aid in understanding resistance. These topics are closely interrelated, and grasping their connections can provide valuable insights into how resistance functions within electrical systems.

    Additionally, a basic understanding of mathematical concepts, particularly algebra and simple equations, is beneficial when studying resistance. These mathematical skills allow students to work with formulas related to resistance, such as calculating the resistance of a conductor based on its physical properties.

    While not strictly necessary, knowledge of materials science can also enhance one's understanding of resistance. Different materials exhibit varying levels of resistance, and understanding the atomic and molecular structure of materials can shed light on why certain substances are better conductors or insulators than others.

    It's worth noting that the study of resistance often leads to more advanced topics in electrical engineering and physics. As such, a solid grasp of resistance can serve as a stepping stone to understanding more complex concepts like capacitance, inductance, and alternating current circuits.

    In conclusion, while there are no specific prerequisites listed for the study of resistance, a strong foundation in basic physics, mathematics, and electrical concepts can greatly enhance your understanding of this important topic. As you delve into the subject of resistance, you'll find that it connects to many other areas of electrical engineering and physics, making it a crucial concept to master for further studies in these fields.