1. Home
  2. >Physics
  3. >Momentum
Help

Momentum and impulse

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

Get the most by viewing this topic in your current grade. Pick your course now.

?
Intros
Lessons
  1. Introduction to impulse and momentum:
  2. What is impulse?
  3. Derivation of impulse from Newton's second law
  4. Impulse equations, units
?
Examples
Lessons
  1. Impulse = F⃗\bold{\vec{F}} ∙ Δt=Δp⃗\bold{\Delta t = \Delta \vec{p}}
    1. A tennis ball is initially at rest, then hit by a racket with 30.0 N [E]. The racket is in contact with the ball for 0.070 s. Find the impulse given to the ball by the racket, and the final momentum of the ball.
    2. A go kart has momentum 1000 kg·m/s forward when the engine applies a force of 55 N forwards for 6 s. Find the impulse given to the go kart by the engine and the final momentum of the go kart.
    3. A baseball is pitched with momentum 5.85 kg·m/s [S], and is hit by a bat which applies a force of 300 N [N]. The bat is in contact with the ball for 0.05 s. Find the impulse given to the ball and the final momentum of the ball.
  2. Impulse = F⃗\bold{\vec{F}} ∙ Δt=m(v⃗f−v⃗i)\bold{\Delta t = m(\vec{v}_f - \vec{v}_i )}
    1. A 1.25 kg skateboard rolls forward at 0.60 m/s. It is given a push forward with a force of 5.0 N for 1.2 s. What is the final velocity of the skateboard?
    2. A soccer ball is initially at rest. Kicking the ball with an impulse 1.30 N·s causes the ball to move at 3.00 m/s. What is the mass of the ball?
    3. A 0.035 kg rubber ball is thrown at a wall at 13 m/s and rebounds at 7 m/s. Find the impulse given to the ball by the wall.
    4. A 1200 kg car travels at 11 m/s [E]. At t = 5.0 s, the driver starts accelerating with a force of 300 N [E] applied to the car. If the final velocity of the car is 17 m/s, what is the time when the driver stops accelerating?
    5. A 50 kg ice skater glides without friction at 7.2 m/s [W] when he skates through a rough patch on the ice for 3.0 s. If his velocity after the patch is 4.5 m/s [W], what is the average force of friction experienced in the patch?
  3. Impulse of stopping a car

    A 1300 kg car travelling at 13.5 m/s [E] can be stopped in 20 s with gentle braking, 4.3 s in a panic stop, and 0.78 s if it hits a wall.

    1. What is the impulse given to the car to stop it in each case?
    2. What is the average force experienced by the car in each case?
    1. Impulse = area under F  vs  t\bold{F\;\mathrm{vs}\; t} graph, during the time interval Δt \bold{\Delta t}
      1. A 0.060 kg golf ball is struck by a golf club which exerts the force shown in the graph over a period of 0.001 s in the forward direction. Find the impulse exerted on the ball, and the final velocity of the ball.
        graph of golf ball F vs t
      2. A 0.425 kg soccer ball is moving 0.80 m/s [E] when it is kicked and experiences the force shown in the graph below. The direction of the kick is [W]. Find the final velocity of the ball.
        graph of soccer ball F vs t
      3. Two people begin pushing a cart. The force experienced by the cart is shown in the graph. At t = 5 s, person A lets go of the cart. At t = 12 s, person B lets go of the cart. Find the impulse person B gives the cart during the time he is the only person pushing it.
        graph of cart F vs t
    2. Momentum and Impulse in two dimensions
      1. A 1300 kg car travelling 12 m/s [W] is given a 1.6×104 N·s [N] impulse. What is the final velocity of the car?
      2. A 1.40 kg ball rolling 8.00 m/s [N] hits a barrier and bounces off, then moving 6.20 m/s [E]. What was the impulse given to the ball?
      3. A 0.25 kg billiard ball in motion is given an impulse of 0.78 N·s [E]. If the final velocity of the ball is 3.2 m/s [27° S of E], what was the initial velocity of the ball?
    Topic Notes
    ?

    In this lesson, we will learn:

    • What is impulse?
    • Derivation of impulse from Newton's second law
    • Impulse equations, units
    • Problem solving with impulse and momentum
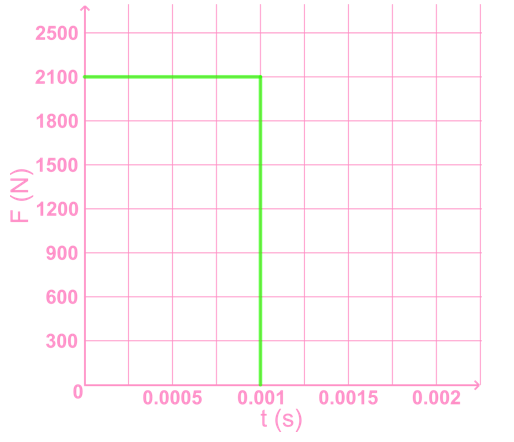
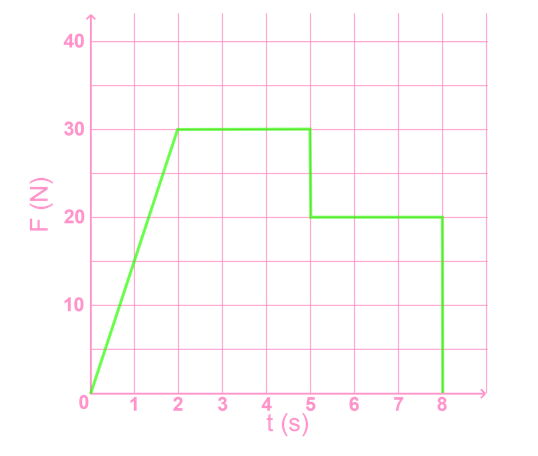
    • Problem solving with F vs t graph

    Notes:

    • Impulse is change in an object's momentum.
    • To change an object's momentum, an impulse must be given to that object. An example would be kicking a soccer ball (an impulse) to set it into motion (give it momentum).
    • An impulse is defined as a force that acts on an object for a period of time.
    • In a graph of force vs. time, the area under the graph is impulse.

    Momentum

    p⃗=mv⃗\vec{p} = m \vec{v}

    p⃗:\vec{p}: momentum, in kilogram meters per second (kg∙m/s)

    m:m: mass, in kilograms (kg)

    v⃗:\vec{v}: velocity, in meters per second (m/s)


    Impulse

    J⃗=F⃗Δt=Δp⃗=m(v⃗f−v⃗i\vec{J} = \vec{F} \Delta t = \Delta \vec{p} = m( \vec{v}_f - \vec{v}_i)

    J⃗:\vec{J}: impulse, in newton seconds (N∙s)

    F⃗:\vec{F}: net force acting on an object, in newtons (N)

    Δt:\Delta t: the length of time for which the force acts, in seconds (s)

    Δp⃗:\Delta \vec{p}:change in momentum of an object, in kilogram meters per second (kg∙m/s)