Force on electric charge moving in a magnetic field 

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

?
Intros
Lessons
  2. The magnitude of the electromagnetic force
  3. The direction of the electromagnetic force
  4. The radius of the motion of moving charged particle in a magnetic field.
?
Examples
Lessons
  1. The path of a charged particle in a uniform magnetic field is circular when the initial velocity is perpendicular to the field.

    Force on Electric Charge Moving in a Magnetic Field


    Which of the following are a valid expression for the radius of this orbit in terms of the magnetic field strength, and the particle's momentum and charge?

    1. BqpBqp
    2. Bpq\frac{Bp}{q}
    3. Bqp\frac{Bq}{p}
    4. pBq\frac{p}{Bq}
    1. A beam made up of ions of various charges and masses enters a uniform magnetic field as shown.

      Force on Electric Charge Moving in a Magnetic Field


      One type of ion is observed to follow path 2. Which path describes the one taken by an oppositely charged ion with twice the mass and twice the charge? (Assume all ions have the same speed.)

      1. Path 1
      2. Path 3
      3. Path 4
      4. Path 5
      1. One method for determining masses of heavy ions involves timing their orbital period in a known magnetic field.
        What is the mass of a single ion that makes 7.0 revolutions in 1.3 × 10-3ss in a 4.5 × 10-2 TT filed?
        1. A positively charged object (qq =1.6 ×10-19 CC) is traveling at 1.9 × 104m/s perpendicular to a 1.0 × 10-3 TT magnetic field. If the radius of the resulting oath is 0.40m, what is the object's mass?

          1. 3.4 × 10-27 kg
          2. 3.1 × 10-19 kg
          3. 2.1 × 10-9 kg
          4. 0.77kg
          Topic Notes
          ?

          In this lesson, we will learn:

          • Magnitude and direction of an electromagnetic force exerted on moving charge in a magnetic field.
          • The radius of the circular motion of a moving charged particle.

          Notes:

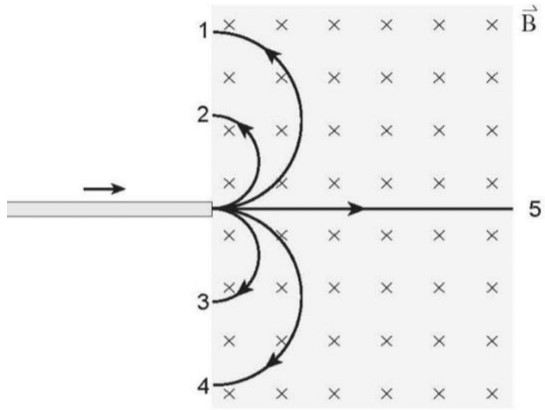
          • A current-carrying wire experience a force when is placed in a magnetic field, similarly, freely moving charged particles would also experience a force when passing through a magnetic field.
          • The magnitude of the electromagnetic force exerted on moving charge in a magnetic field is calculated using the following equation:

            F=qvBsin⁡θF = qvB \sin \theta

          qq = quantity of charge 
          vv = velocity of moving charge 
          BB = magnetic field 
          θ\theta = the angle between B→ \overrightarrow{B} and v→ \overrightarrow{v}

          • The force is greatest when the angle between B→ \overrightarrow{B} and v→ \overrightarrow{v} is 90°, Fmax=qvB \qquad F_{max} = qvB
          • The force is zero if the particle moves parallel to the field lines and the angle between B→ \overrightarrow{B} and v→ \overrightarrow{v} is 0°

          • The direction of the force is perpendicular to the magnetic field B→ \overrightarrow{B} and to the velocity v→ \overrightarrow{v} of the particle. 
          • The direction of the force is found using the right-hand rule, fingers point along the direction of the particle’s velocity and bend your fingers towards the of B→ \overrightarrow{B} . Then your thumb will point in the direction of the force. This is true only for positively charged particles, for negatively charged particles, the force is in exactly the opposite direction.

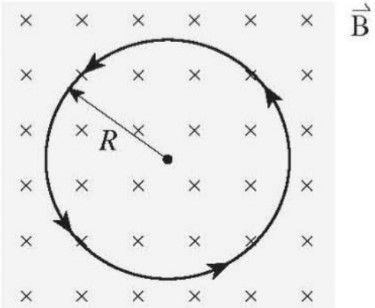
          Force on Electric Charge Moving in a Magnetic Field

          • The force exerted by a uniform magnetic field on a moving charged particle, produces a circular path.

          “The diagram below represents the direction of the force exerted on an electron”


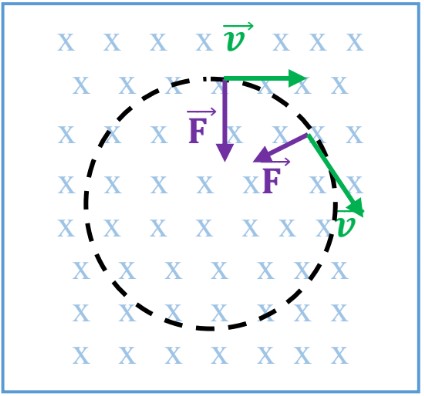
          Force on Electric Charge Moving in a Magnetic Field

          • The particle would move in a circular path with constant centripetal acceleration if the force is always perpendicular to its velocity, a=v2ra = \frac{v^{2}}{r}
          • The force is greatest when the angle between B→ \overrightarrow{B} and v→ \overrightarrow{v} is 90°, Fmax=qvB \qquad F_{max} = qvB


            • ∑F=ma \sum F = ma

            qvB=mv2rqvB = m \frac{v^{2}}{r}

            r=mvqB r = \frac{mv} {qB}

            Since F→ \overrightarrow{F} is perpendicular to v→ \overrightarrow{v} , the magnitude of v→ \overrightarrow{v} does not change. From this equation, we see that if B→ \overrightarrow{B} = constant, then rr = constant, and the curve must be a circle.