Sign In
Sign Up
flag-us

Elastic vs Inelastic Collisions: Mastering Fundamental Physics
Dive into the world of collision physics! Explore energy conservation, momentum, and real-world applications. Enhance your problem-solving skills and grasp key physics concepts with our comprehensive guide.

Get the most by viewing this topic in your current grade. Pick your course now.

Now Playing:Elastic and inelastic collisions – Example 0a
Intros
  1. Introduction to elastic and inelastic collisions
  2. Introduction to elastic and inelastic collisions
    Meaning of elastic and inelastic collisions
  3. Introduction to elastic and inelastic collisions
    What happens to kinetic energy in a collision?
Examples
  1. Solving word problems with momentum and elastic/inelastic collisions
    1. Two cars collide head-on and stick together. The cars are stationary after colliding.
      1. Is total momentum conserved?
      2. Is total energy conserved?
      3. Is the collision elastic or inelastic?

    2. Identify each situation as an inelastic or elastic collision.
      1. One car crashes into another, bouncing apart with a loud bang.
      2. A hammer strikes a piece of steel, bouncing off and producing sparks.
      3. A He atom collides with a H atom, bouncing off and maintaining overall kinetic energy.

Momentum and motion
Jump to:NotesConceptExampleFAQsPrerequisites
Notes

In this lesson, we will learn:

  • Meaning of elastic and inelastic collisions
  • What happens to kinetic energy in a collision?
  • Understanding perfectly inelastic collisions
  • Problem solving with elastic and inelastic collisions

Notes:

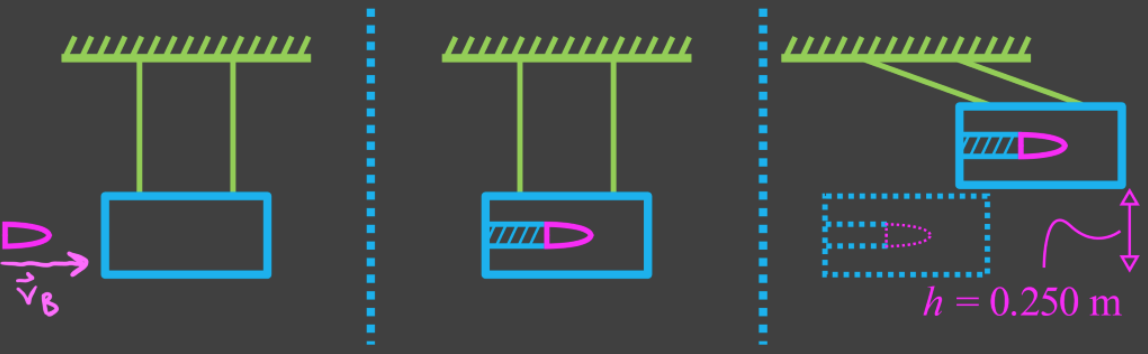
  • Total momentum and total energy are conserved in collisions. However, kinetic energy is not always conserved, since it can be converted into other forms of energy.
  • Elastic collision: collision where no kinetic energy is lost
  • Inelastic collision: collision where part of the kinetic energy is converted to other forms of energy
  • Perfectly inelastic collision: collision where the maximum possible amount of kinetic energy is converted to other forms of energy; objects stick together.

Conservation of Momentum

∑p⃗i=∑p⃗f\sum\vec{p}_i = \sum\vec{p}_f

p⃗i:\vec{p}_i: initial momentum, in kilogram meters per second (kg·m/s)

p⃗f:\vec{p}_f: final momentum, in kilogram meters per second (kg·m/s)


Conservation of Energy

∑E⃗i=∑E⃗f\sum\vec{E}_i = \sum\vec{E}_f

E⃗i:\vec{E}_i: initial energy, in joules (J)

E⃗f:\vec{E}_f: final energy, in joules (J)


Kinetic Energy

KE=12mv2KE = \frac{1}{2}mv^2

KE:KE: kinetic energy, in joules (J)

m:m: mass, in kilograms (kg)

v:v: speed, in meters per second (m/s)


Potential Energy

PE=mghPE = mgh

PE:PE: potential energy, in joules (J)

g:g: acceleration due to gravity, in meters per second squared (m/s2)

h:h: height, in meters (m)

Concept

Introduction to Elastic and Inelastic Collisions

Elastic and inelastic collisions are fundamental concepts in physics that describe how objects interact when they collide. In an elastic collision, both momentum and kinetic energy are conserved, resulting in objects bouncing off each other with no loss of energy. Conversely, inelastic collisions involve a loss of kinetic energy, often resulting in objects sticking together or deforming upon impact. The introduction video provides a clear visual representation of these collision types, making it easier for students to grasp the concept. Understanding elastic and inelastic collisions is crucial in physics as it forms the basis for analyzing various real-world scenarios, from billiard ball interactions to car crashes. By mastering these concepts, students can better comprehend the principles of momentum conservation and energy transfer in physical systems. This knowledge is essential for solving complex problems in mechanics and developing a deeper understanding of how objects behave during collisions in both everyday life and scientific applications.

Example

Understanding the concepts of elastic and inelastic collisions is crucial in physics as it helps explain how objects interact during collisions. This guide will walk you through the meaning of these types of collisions and how they differ in terms of momentum and kinetic energy conservation.

Step 1: Introduction to Collisions

In this section, we will discuss the basic idea of collisions. When objects collide, their momentum is conserved. However, the way momentum is conserved can vary. Sometimes objects bounce apart after a collision, and other times they stick together. This difference in behavior is explained by the concept of elasticity in collisions.

Step 2: Understanding Elastic Collisions

Elastic collisions are those in which the total kinetic energy of the system is conserved before and after the collision. For example, when bumper cars collide, they bounce apart, and their kinetic energy remains the same. This type of collision is characterized by the fact that the sum of the initial kinetic energies of the colliding objects is equal to the sum of their final kinetic energies.

Step 3: Understanding Inelastic Collisions

Inelastic collisions, on the other hand, are those in which some of the kinetic energy is lost during the collision. This lost energy is usually converted into other forms of energy such as heat or sound. For instance, when regular cars collide, they often stick together and come to a stop, indicating that kinetic energy has been lost. In this type of collision, the sum of the initial kinetic energies is not equal to the sum of the final kinetic energies.

Step 4: Conservation of Momentum

Regardless of whether a collision is elastic or inelastic, the total momentum of the system is always conserved. This means that the sum of the initial momenta of the colliding objects is equal to the sum of their final momenta. For example, if two bumper cars with equal and opposite momenta collide, their total momentum before and after the collision remains zero.

Step 5: Real-Life Examples

To better understand these concepts, consider the collision between bumper cars and regular cars. Bumper cars are designed to be elastic, meaning they bounce apart after a collision, conserving kinetic energy. Regular cars, however, are designed with crumple zones to absorb kinetic energy during a collision, making the collision inelastic. This design is intended to enhance safety by reducing the force of impact on the passengers.

Step 6: Kinetic Energy Calculations

In an elastic collision, the kinetic energy before and after the collision can be calculated using the formula KE = 1/2 mv^2. For two colliding bumper cars, the total initial kinetic energy is the sum of their individual kinetic energies. After the collision, the total final kinetic energy remains the same. In an inelastic collision, the initial kinetic energy is also the sum of the individual kinetic energies, but the final kinetic energy is less due to the conversion of some kinetic energy into other forms.

Step 7: Conclusion

In summary, the key difference between elastic and inelastic collisions lies in the conservation of kinetic energy. Elastic collisions conserve kinetic energy, while inelastic collisions do not. However, in both types of collisions, the total momentum of the system is conserved. Understanding these principles is essential for analyzing and predicting the outcomes of collisions in various physical systems.

FAQs

  1. What is the difference between an elastic and an inelastic collision?

    An elastic collision conserves both kinetic energy and momentum, with objects bouncing apart without deformation. In contrast, an inelastic collision only conserves momentum, with some kinetic energy converted to other forms like heat or deformation energy. Objects may stick together or deform in inelastic collisions.

  2. How do you calculate if a collision is elastic or inelastic?

    To determine if a collision is elastic or inelastic, calculate the total kinetic energy before and after the collision. If the total kinetic energy remains the same (within experimental error), it's elastic. If there's a decrease in kinetic energy, it's inelastic. You can use the formula KE = ½mv² for each object and compare the sums.

  3. Do inelastic collisions always result in objects sticking together?

    Not always. While perfectly inelastic collisions result in objects sticking together, many inelastic collisions are partially inelastic. In these cases, objects may separate after collision but with a loss of kinetic energy. The degree of "stickiness" depends on the collision's inelasticity.

  4. What are examples of inelastic collisions?

    Examples of inelastic collisions include car crashes, a ball dropping on the floor, a hammer striking a nail, two pieces of clay colliding and sticking together, and a meteor impact on a planet's surface. In each case, some kinetic energy is converted to other forms like heat, sound, or deformation energy.

  5. How does the concept of elastic and inelastic collisions apply in real-world scenarios?

    These concepts are crucial in various fields. In automotive engineering, understanding inelastic collisions helps design safer vehicles with effective crumple zones. In sports, elastic collision principles are used to improve equipment like tennis rackets and golf clubs. In particle physics, collision concepts are fundamental to experiments in particle accelerators, advancing our understanding of matter and energy.

Prerequisites

Understanding elastic and inelastic collisions requires a solid foundation in several key physics concepts. These prerequisite topics are crucial for grasping the intricacies of collision dynamics and their outcomes. One of the most fundamental principles to master is the conservation of energy. This concept is essential because it governs how energy is transferred and transformed during collisions, particularly the conservation of kinetic energy in elastic collisions.

Equally important is the conservation of momentum in one dimension. This principle is critical for analyzing both elastic and inelastic collisions, as momentum is always conserved regardless of the collision type. Understanding how momentum is transferred between objects during a collision is key to predicting the final velocities and directions of the colliding bodies.

Another relevant concept is electric potential and electric potential energy. While this may seem less directly related, it's important for understanding the concept of elastic potential energy, which plays a role in elastic collisions. In elastic collisions, objects temporarily deform and store energy as elastic potential energy before returning to their original shape.

These prerequisite topics form the foundation for understanding elastic and inelastic collisions. The conservation of energy principle helps students differentiate between elastic collisions, where kinetic energy is conserved, and inelastic collisions, where some kinetic energy is converted to other forms. The conservation of momentum allows for accurate calculations of post-collision velocities in both types of collisions.

Moreover, grasping these concepts enables students to analyze more complex scenarios, such as collisions involving springs or electromagnetic interactions. The understanding of elastic potential energy, derived from the study of electric potential energy, becomes crucial when examining the temporary deformation of objects during elastic collisions.

By mastering these prerequisite topics, students can develop a comprehensive understanding of elastic and inelastic collisions. They will be able to predict collision outcomes, calculate energy transfers, and analyze real-world applications of collision physics. This knowledge is not only essential for academic success in physics but also for understanding many practical applications in engineering, sports science, and even everyday phenomena like car crashes or billiard ball collisions.

In conclusion, a strong grasp of conservation of energy, conservation of momentum, and the concepts of potential energy forms the bedrock for comprehending elastic and inelastic collisions. These fundamental principles intertwine to provide a complete picture of collision dynamics, enabling students to tackle complex problems and gain deeper insights into the fascinating world of physics.