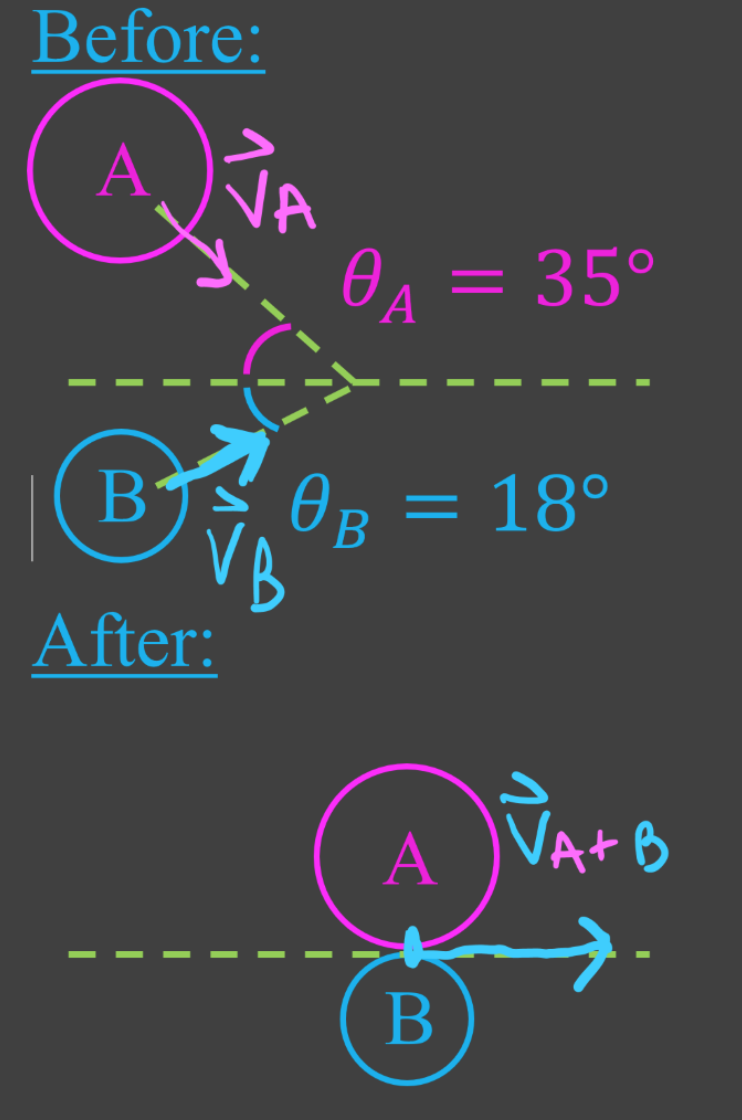Conservation of momentum in two dimensions

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

Get the most by viewing this topic in your current grade. Pick your course now.

?
Intros
Lessons

  1. Introduction to conservation of momentum in two dimensions

    • Review of conservation of momentum
    • Vector nature of momentum and conservation of momentum
?
Examples
Lessons
  1. ∑p⃗i=∑p⃗f:\bold{\sum\vec{p}_i = \sum\vec{p}_f}: Objects that bounce apart after collision in two dimensions
    1. 1.25 kg ball A is moving at 3.40 m/s [E] when it strikes stationary 1.00 kg ball B. After the collision, ball A moves off at an angle of [60.0° N of E], and ball B moves off at an angle of [30.0° S of E]. Find the velocities of A and B after collision.
      before and after of balls A and B collision
    2. 1.10 kg puck A travelling at 2.00 m/s [E] collides with 0.860 kg puck B moving 0.400 m/s [W]. After the collision, puck A moves off at 1.60 m/s [40.0° N of E]. Find the velocity of puck B.
      before and after of objects that bounce apart after collision example b
  2. ∑p⃗i=∑p⃗f:\bold{\sum\vec{p}_i = \sum\vec{p}_f}: Objects that stick together after collision in two dimensions
    1. 1100.0 kg car A travelling at 12.0 m/s [E] collides with 975 kg car B travelling 19.0 m/s [N]. The cars stick together. Find the velocity of the two vehicles after collision.
    2. 0.50 kg magnetic puck A travelling at 1.1 m/s collides with 0.35 kg puck B travelling with an unknown velocity, as shown in the diagram. The two pucks stick together and travel due [E]. Find the initial velocity of the second puck. before and after of pucks sticky collision
  3. ∑p⃗i=∑p⃗f:\bold{\sum\vec{p}_i = \sum\vec{p}_f}: Objects that explode apart in two dimensions
    1. A bomb initially at rest explodes, sending three fragments in different directions as shown in the diagram. Find the velocity of the 0.71 kg fragment.
      bomb explosion fragments

    2. A 21.0 kg child holding a 0.755 kg snowball rides a 3.00 kg sled on a frictionless ice surface at 2.50 m/s [E]. The child throws the snowball, giving it an impulse due [N] relative to the sled. The snowball travels at 6.00 m/s immediately after it is thrown.

    3. Balls A, B, and C roll together as shown in the diagram, with all three balls colliding at the same time. Find the mass of ball C if the 3 balls are stationary after colliding.
      balls A, B, and C collision
    4. A spacecraft with a total mass of 8620 kg is travelling through space at a speed of 156 m/s. Control wants to adjust its direction by 25.0°, and increase its speed to 175 m/s. Gas is ejected though a thruster on the side of the craft, travelling at 85.0° clockwise from the craft's original direction of motion. Find the mass of gas ejected.
      spacecraft thrusting
Topic Notes
?

In this lesson, we will learn:

  • Review of conservation of momentum
  • Vector nature of momentum and conservation of momentum
  • Problem solving with conservation of momentum in two dimensions

Notes:

  • Momentum is a conserved quantity and a vector.
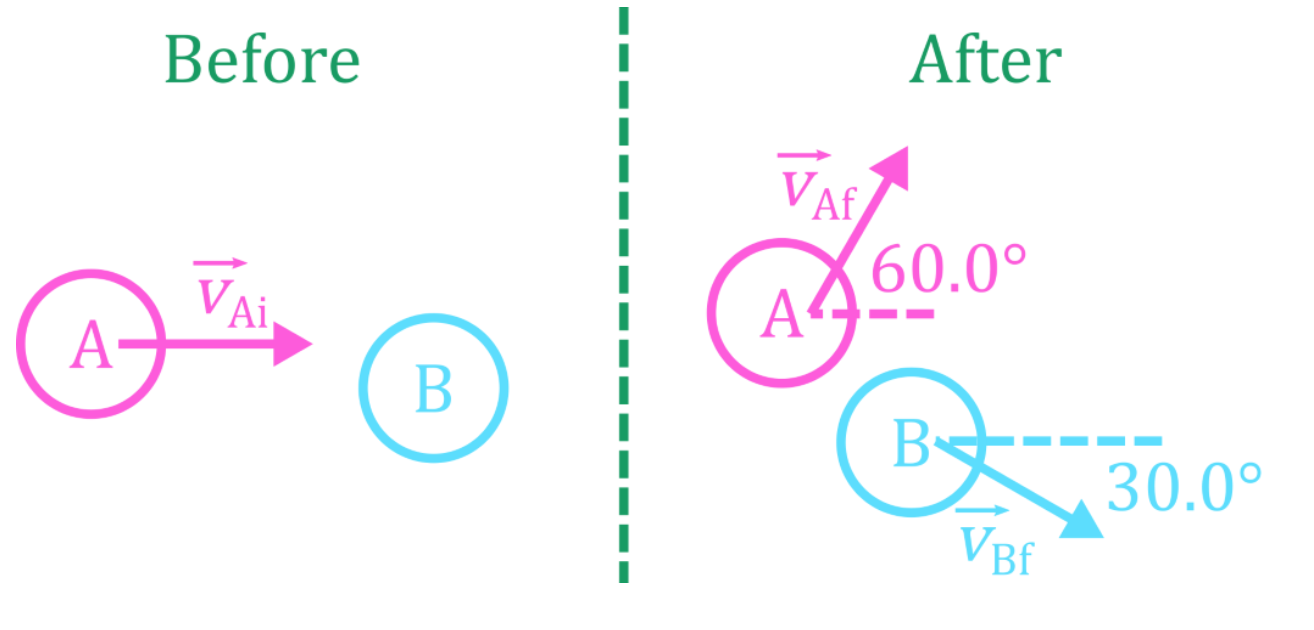
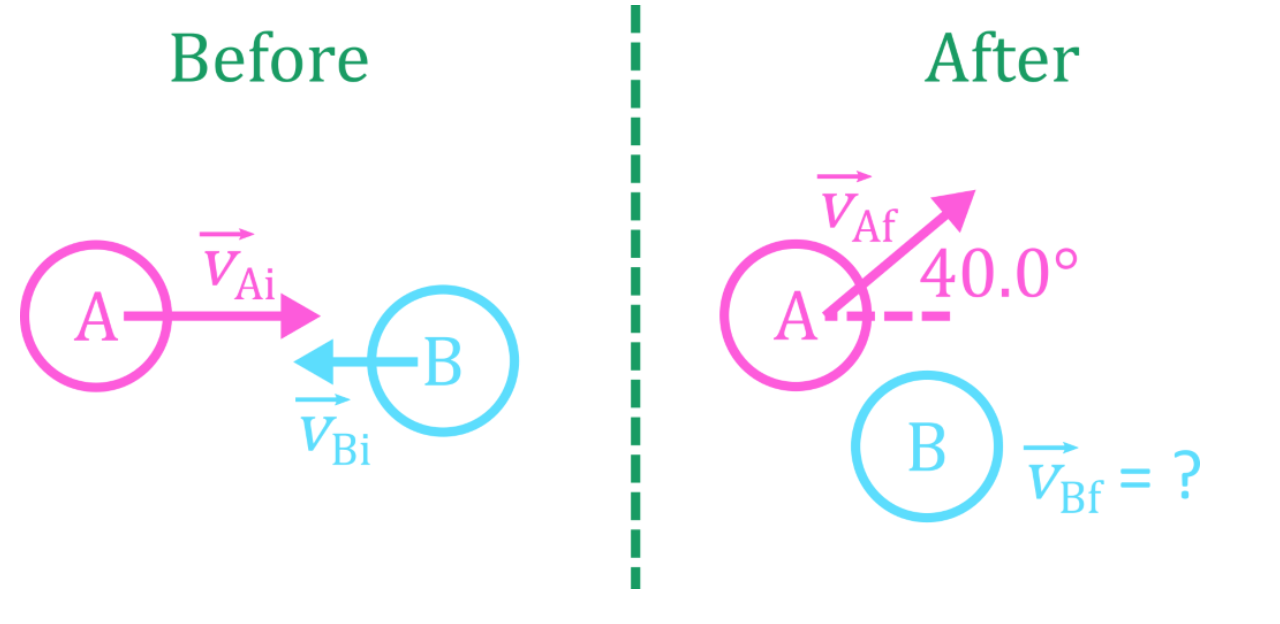
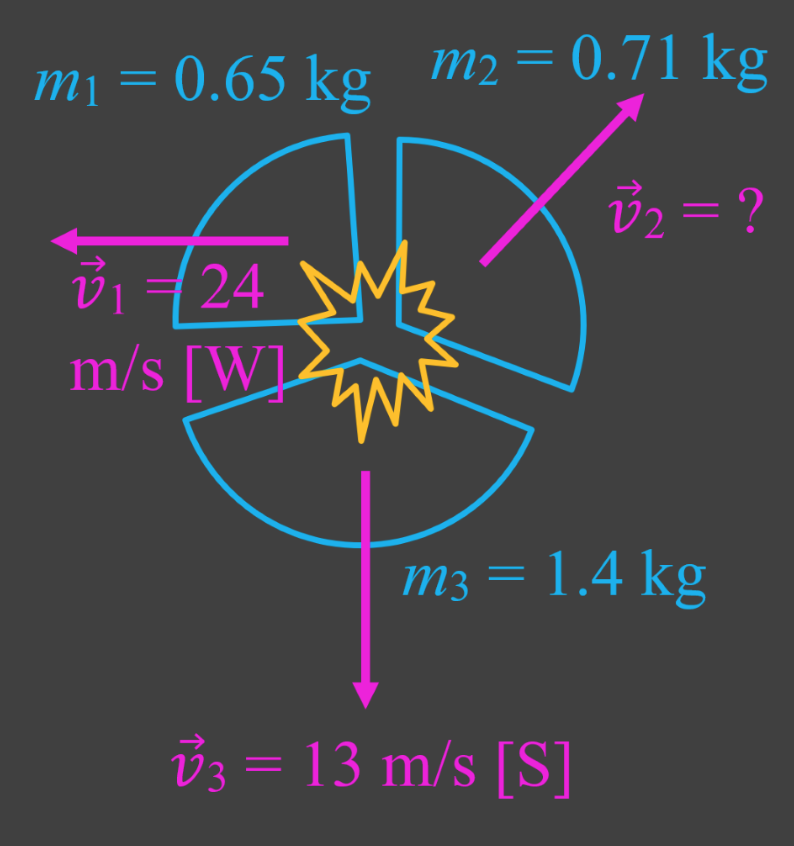
    • In a collision between a set of objects, total momentum of the objects before collision = total momentum after collision.
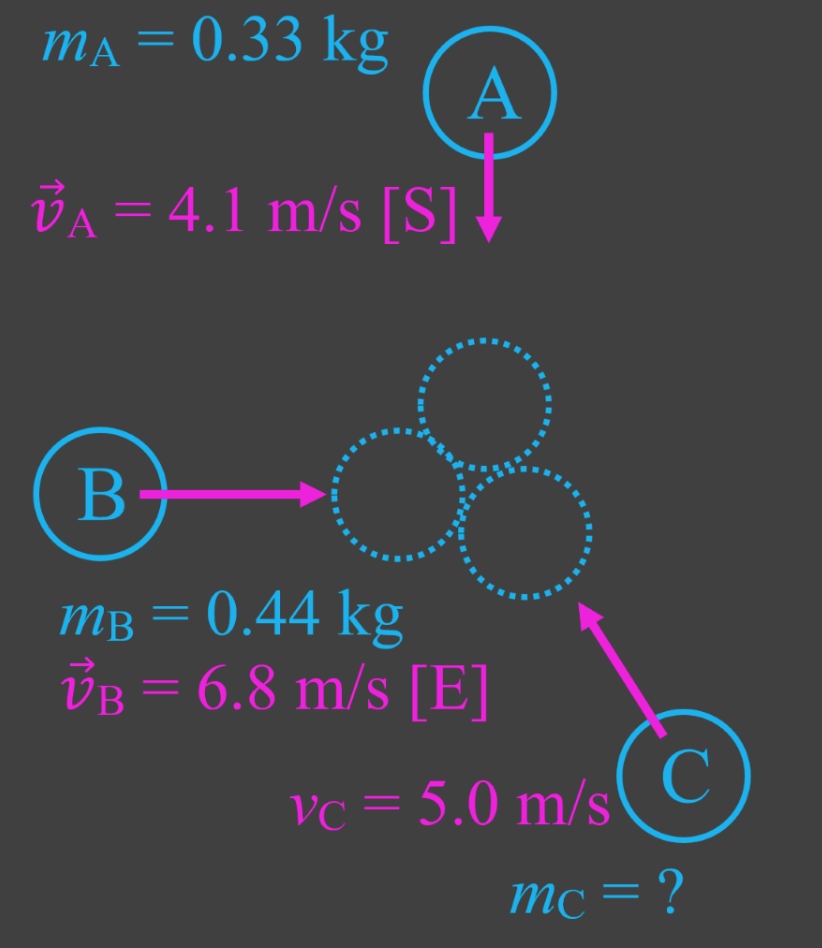
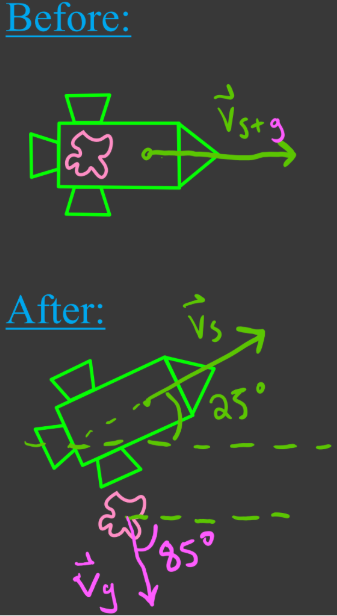
    • When using conservation of momentum on objects that move in two dimensions, use vector addition (tip-to-tail method).

Momentum

p⃗=mv⃗:\vec{p} = m \vec{v}: momentum, in kilogram meters per second (kg∙m/s)

m:m: mass, in kilograms (kg)

v⃗:\vec{v}: velocity, in meters per second (m/s)


Impulse

J⃗=F⃗Δt=Δp⃗=mΔv⃗\vec{J} = \vec{F} \Delta t = \Delta \vec{p} = m\Delta \vec{v}

J⃗:\vec{J}: impulse, in newton seconds (N∙s)

F⃗:\vec{F}: force, in newtons (N)

t⃗:\vec{t}: time, in seconds (s)


Conservation of Momentum

∑p⃗i=∑p⃗f\sum\vec{p}_i = \sum\vec{p}_f

p⃗i:\vec{p}_i: initial momentum, in kilogram meters per second (kg·m/s)

p⃗f:\vec{p}_f: final momentum, in kilogram meters per second (kg·m/s)


Law of Sines

asinA=bsinB=cSinC\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{SinC}
a,b,c: length of sides a,b,c
A,B,C: angles opposite sides a, b, c

Law of Cosines

c2=a2+b2−2ab cosCc^2 = a^2 + b^2 - 2ab \,cosC