Sign In
Sign Up
flag-us

Circuitry Problem Solving: From Basics to Advanced Techniques
Dive into the world of circuitry problem solving. Master essential concepts, analyze complex circuits, and develop critical thinking skills for real-world applications in electrical engineering.

Now Playing:Circuitry problem solving – Example 0a
Intros
  1. Introduction to Circuitry Problem Solving:
  2. Introduction to Circuitry Problem Solving:
    A crash course review on electric circuits.
  3. Introduction to Circuitry Problem Solving:
    Concept 1: How are individual resistances related to voltage drops?
Examples
  1. Problem Solving for Resistors and Voltage Drops
    The two circuits below are configured as shown. Circuit B includes an additional resistor R3 placed in parallel with R1. Compare the values of VR1 and VR2 in circuit BB compared to circuit AA (no change, decrease, increase)?

    Circuitry Problem Solving
    Voltage
    Jump to:NotesConceptFAQsPrerequisites
    Notes

    In this lesson, we will learn:

    • A brief review on voltage, current, and resistance
    • Establishing 4 main concepts for problem solving:
      • Concept #1: a smaller resistor uses up less voltage; a bigger resistor uses up more voltage
      • Concept #2: the more resistors added in series with the battery into the circuit will increase the total equivalent resistance
      • Concept #3: the more resistors added in parallel with the circuit will decrease the total equivalent resistance
      • Concept #4: the brightness of a lightbulb is related to the voltage drop across it (as well as the power dissipated by it)
    • Solving questions for more conceptual electric circuits questions:
      • Using a combination of all previous concepts and formulas (V,I,R,V, I, R, Ohm’s Law, VtermV_{term}, Power)
      • As well as applying the 4 main concepts

    Notes:

    • Before facing problem solving questions for electric circuits that are oftentimes just as conceptual as they are mathematical, one must have a firm understanding of the concepts of each lesson thus far:
      • Voltage: staircase analogy, Kirchhoff’s Loop Rule, equal voltage in parallel
      • Current: water analogy, Kirchhoff’s Junction Rule
      • Resistance: calculating total resistance for series vs. parallel configurations
        • Req(series)=R1+R2+R3+...Rn=∑k=1nRk R_{eq (series) = R_{1} + R_{2} + R_{3} + ... R_{n} = \sum_{k = 1}^n R_{k}}
        • 1Req(parallel)=1R1+1R2+1R3+...1Rn=∑k=1n1Rk \frac{1}{R_{eq (parallel)}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + . . . \frac{1}{R_{n}} = \sum_{k = 1}^n \frac{1}{R_{k}}
      • The conceptual relationships as defined by Ohm’s Law: V=IRV=IR
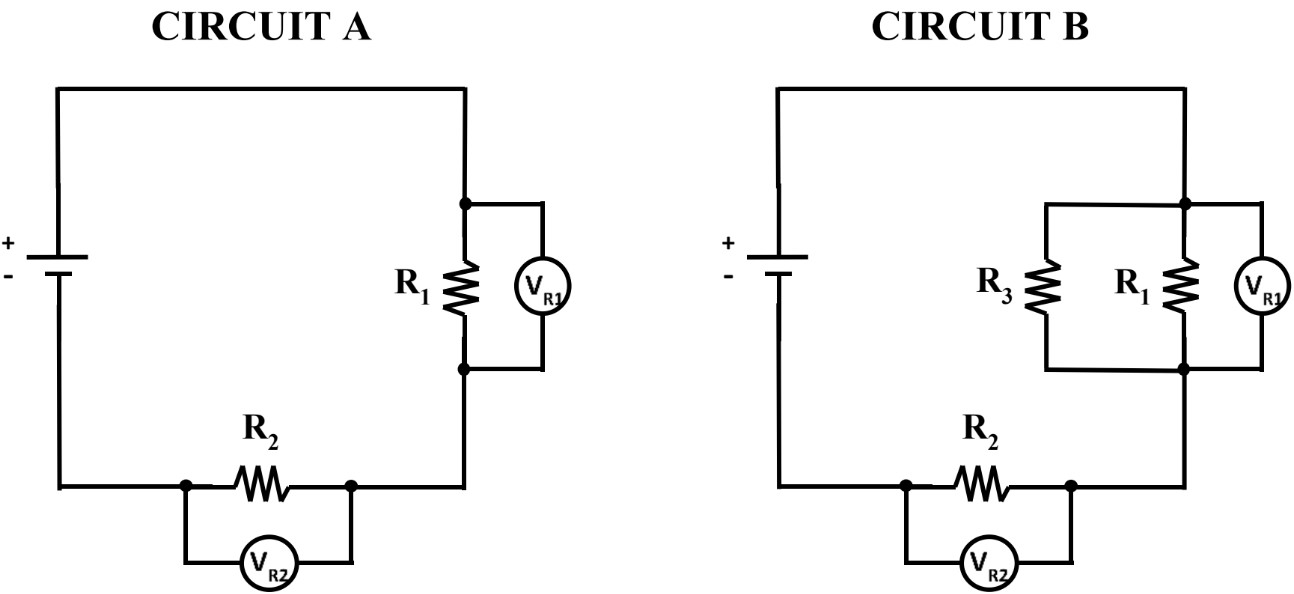
      • The shortcut for Ohm’s law; the voltage divider method: Vx=Vtotal⋅RxRtotalV_{x} = V_{total} \cdot \frac{R_{x}}{R_{total}}
      • The concept of terminal voltage and calculations: Vterm=ϵ−IrV_{term} = \epsilon - Ir
      • Power: total power is additive, P=EtP = \frac{E}{t} and P=IV=I2R=V2RP = IV = I^{2}R = \frac{V^{2}}{R}
      • Energy: E=PtE=P t and E=IVtE=I V t

    • The 4 main concepts can be summarized as follows:
      • I. The greater the resistance of a resistor, the more voltage that it uses up (and vice versa; a smaller resistor uses less voltage)
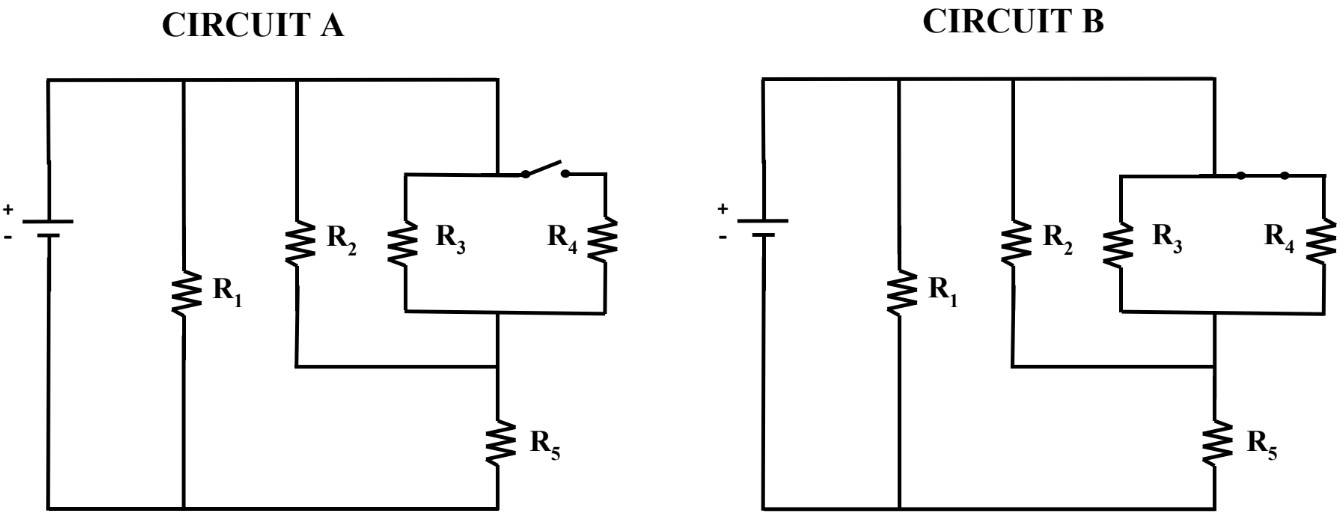
      • II. The more resistors added in series, the greater the equivalent resistance
      • III. The more resistors added in parallel, the lesser the equivalent resistance
      • IV. The brightness of a lightbulb is related to the voltage it uses up (its voltage drop) as well as, the power dissipated by it

    • The brightness of a lightbulb is related to the amount of voltage that it uses up (voltage drop); the more voltage used, the brighter the light bulb
      • The voltage drop is dependent on current and resistance (V=IRV=IR)
    • The brightness of a lightbulb can also be understood as how hot the filament is burning
      • The incandescent lightbulb is transforming electrical energy into thermal and light energy; the rate of energy transformation is power
      • Power is dependent on voltage (P=IVP=I V) as well as current and resistance (P=I2R=V2RP=I^{2}R= \frac{V^{2}}{R} )
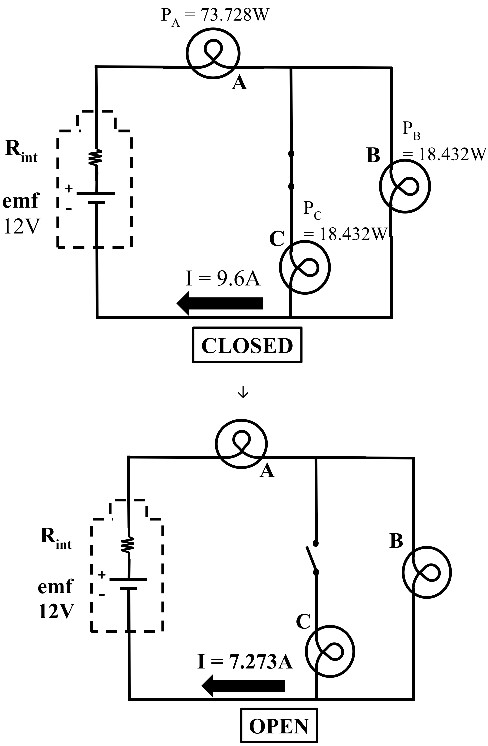
    • When observing lightbulbs in series:
      • Adding more lightbulbs in series will increase the overall resistance, thus diminishing the total current—this leads to a smaller voltage drop across each lightbulb, causing a dimming effect
      • Opening a switch or having a single broken lightbulb in the series chain will cause all relevant lightbulbs turn off (the whole circuit will be compromised)
    • When observing lightbulbs in parallel:
      • Adding more lightbulbs in parallel will decrease the overall resistance, thus increasing the total current—the balance leads to relatively constant brightness across all parallel lightbulbs
      • Opening a switch or having a single broken lightbulb will not compromise the whole circuit; only the relevant branch of the circuit will be affected (turned off)
    Concept

    Introduction to Circuitry Problem Solving

    Welcome to the fascinating world of circuitry problem solving! As your math tutor, I'm excited to guide you through this essential aspect of electrical engineering. To kick things off, we'll start with an introduction video that lays the groundwork for understanding key concepts. This video is crucial as it visually demonstrates how circuits work and the basic principles behind problem-solving in this field. As we delve deeper, you'll learn to analyze circuits, calculate voltages and currents, and troubleshoot common issues. Remember, circuitry problem solving is like solving a puzzle it requires patience, logical thinking, and a step-by-step approach. Don't worry if it seems challenging at first; with practice, you'll become more comfortable tackling these problems. The skills you'll develop here are invaluable, not just for academics but also for real-world applications in electronics and engineering. Let's embark on this exciting journey together, unraveling the mysteries of circuits one problem at a time!

    FAQs

    Here are some frequently asked questions about circuitry problem solving:

    1. What is Ohm's Law and how is it used in circuit analysis?

      Ohm's Law states that the current through a conductor between two points is directly proportional to the voltage across the two points. It is expressed as V = IR, where V is voltage, I is current, and R is resistance. This fundamental law is used extensively in circuit analysis to calculate unknown values, determine power consumption, and analyze circuit behavior.

    2. How do series and parallel circuits differ in terms of total resistance?

      In a series circuit, the total resistance is the sum of all individual resistances (Rtotal = R1 + R2 + R3 + ...). In a parallel circuit, the reciprocal of the total resistance is equal to the sum of the reciprocals of individual resistances (1/Rtotal = 1/R1 + 1/R2 + 1/R3 + ...). This means that adding resistors in series increases total resistance, while adding them in parallel decreases it.

    3. What are Kirchhoff's Laws and when should they be applied?

      Kirchhoff's Laws consist of two principles: the Current Law (KCL) and the Voltage Law (KVL). KCL states that the sum of currents entering a node equals the sum of currents leaving it. KVL states that the sum of all voltages around any closed loop in a circuit must equal zero. These laws are particularly useful when analyzing complex circuits with multiple loops or nodes.

    4. How can I determine the brightness of light bulbs in different circuit configurations?

      The brightness of a light bulb depends on the power it receives, which is related to the voltage across it and the current flowing through it. In a series circuit, the voltage is divided among the bulbs, making them dimmer than if they were connected alone. In a parallel circuit, each bulb receives the full voltage, maintaining full brightness. The specific brightness can be calculated using the power formula P = VI or P = I²R.

    5. What are some practical applications of circuit analysis in everyday life?

      Circuit analysis has numerous practical applications, including: designing and troubleshooting electronic devices like smartphones and computers, optimizing energy efficiency in home appliances, developing renewable energy systems, improving electric vehicle technology, and automating industrial processes. Understanding circuit principles is crucial for innovation in fields ranging from consumer electronics to large-scale industrial systems.

    Prerequisites

    Understanding the fundamentals is crucial when diving into the world of circuitry problem solving. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a strong foundation in related areas can significantly enhance your ability to tackle complex circuit problems effectively.

    Circuitry problem solving is a multifaceted skill that draws upon various aspects of electrical engineering and physics. To excel in this field, students should consider developing a solid understanding of basic electrical concepts, such as voltage, current, and resistance. These fundamental principles form the backbone of circuit analysis and are essential for identifying and resolving issues in electrical systems.

    Additionally, a firm grasp of mathematics, particularly algebra and trigonometry, can prove invaluable when working with circuit equations and calculations. These mathematical tools enable you to manipulate formulas, solve for unknown variables, and interpret circuit behavior quantitatively.

    Another important aspect of circuitry problem solving is familiarity with various circuit components and their functions. Understanding how resistors, capacitors, inductors, and semiconductors behave within a circuit can greatly aid in diagnosing and troubleshooting issues. This knowledge allows you to predict how changes in one part of a circuit might affect the overall system.

    Moreover, developing skills in logical thinking and systematic approaches to problem-solving can significantly enhance your ability to tackle complex circuitry challenges. This includes learning how to break down large problems into smaller, manageable steps and applying methodical troubleshooting techniques.

    While not explicitly listed as prerequisites, topics such as Ohm's Law, Kirchhoff's Laws, and basic circuit analysis techniques are fundamental to circuitry problem solving. These principles provide a framework for understanding how electrical components interact within a circuit and how to analyze their behavior.

    It's also worth noting that practical experience can be just as valuable as theoretical knowledge. Hands-on experimentation with simple circuits, using tools like breadboards and multimeters, can provide invaluable insights and reinforce theoretical concepts in a tangible way.

    As you progress in your study of circuitry problem solving, you may find it beneficial to explore more advanced topics such as digital logic, signal processing, and electromagnetic theory. These areas can provide deeper insights into complex circuit behaviors and open up new avenues for problem-solving approaches.

    In conclusion, while there may not be a strict list of prerequisites for circuitry problem solving, building a strong foundation in related areas of electrical engineering and physics can significantly enhance your problem-solving capabilities. By continuously expanding your knowledge and skills in these areas, you'll be better equipped to tackle a wide range of circuitry challenges with confidence and expertise.