Sign In
Sign Up
flag-us

Unlock the Secrets of Atomic Orbitals and Energy Levels
Dive into the quantum world of atomic orbitals and energy levels. Understand electron behavior, atomic structure, and the foundations of modern chemistry. Elevate your scientific knowledge with our comprehensive guide.

  1. Intros0/5 watched
  2. Examples0/1 watched
  1. 0/5
  2. 0/1
Now Playing:Atomic orbitals and energy levels – Example 0a
Intros
0/5 watched
  1. What are electron orbitals?
  2. What are electron orbitals?
    What affects molecular/atomic properties?
  3. What are electron orbitals?
    How quantum theory led to electron orbitals.
Examples
0/1 watched
  1. Draw the subshells and write the electron configurations of the following atoms.
    1. Write the electron configurations for the following atoms and draw the shapes of their highest energy occupied subshells:
      1. Fluorine
      2. Helium
      3. Carbon

Atomic orbitals and energy levels
Jump to:NotesConceptExampleFAQsPrerequisites
Notes

In this lesson, we will learn:

  • To understand the experimental evidence that led to our current understanding of electrons and orbitals.
  • To recall the shape and nature of early electron orbitals and energy level diagrams.
  • To fill electron orbitals for the first two rows of elements correctly according to the Pauli and Aufbau principles.

Notes:

  • There are many methods we use to learn about chemical bonding, find out the shape and structure of compounds, but why do atoms even form molecules and compounds in the first place? What causes different molecules to have different shapes?
    VSEPR helps us predict molecular shapes. Recall the shapes of some molecules from Molecular Geometry:
    • BH3 is trigonal planar, but NH3 and PH3, with the same number of atoms, don't form the same shape as BH3.
    • CH4 is tetrahedral and isoelectronic molecules (same number of electrons) like NH3 and water H2O still form the same tetrahedral structure without four H atoms, using their lone electron pairs instead.
    • Some atoms do not form molecules; for some reason they are stable enough to exist as individual atoms, like helium (He).
    • Clearly, it is not the number of atoms or number of electrons that determine molecule shape and other properties, it is the different states electrons are in. Today we use atomic orbitals to describe the behaviour of electrons in atoms.

  • To understand why we use orbitals to describe electrons it is very helpful to know how science got here. Some extremely important experiments and developments were made in the early 20th century. All the developments below led to Nobel Prizes for the scientists contributions to quantum mechanics:
    • In 1900, Max Planck derived Planck’s law, which solved the ultraviolet catastrophe. Classical theory predicted that the emission spectrum of a black body (think of the sun as a rough example) would amount to emitting infinite amounts of UV and other high frequency radiation.
      This is obviously not true; humans wouldn’t exist if it was! By assuming energy is transferred and emitted in quantized amounts, Planck’s revision to the obviously flawed theory correctly fitted real observations.

    • In 1905, Einstein’s experiment, the photoelectric effect, was explained using Planck’s idea of quantization the Planck-Einstein relation, E = hv. Einstein explained that light travels as quantized packets of energy called photons.
      Although light was long considered a wave, it also shows particulate properties.

    • In 1913, Niels Bohr used the quantization of energy to develop his model of the atom. Bohr could explain the atomic emission spectrum (AES) of hydrogen; the electron orbited the nucleus in quantized energy states. If it absorbed energy, an electron would be excited to a higher energy state, before returning to a ground state, emitting a quantized amount of energy (E = hv) in the process. These energy ‘states’ are the electron shells.

    • In 1923, the de Broglie hypothesis proposed that like light, all matter including electrons has wave-particle nature. He developed the de Broglie wavelength formula λ \lambda = h/p, which applies to particles like electrons, relating momentum of a particle to wavelength. Later experiments of electrons diffracting through slits (a wave property) confirmed the wave properties of electrons.

    • In 1927, Werner Heisenberg developed Heisenberg’s uncertainty principle. A simple consequence of wave-particle duality is that we cannot exactly know the location AND momentum of an electron at the same time.
      • Waves have no definitive position; they are continuously spread through space. However, we can identify features of waves like wavelength and frequency, which is related to energy and momentum.
      • Particles definitively exist in one position at a given time, but they do not have a wavelength and as such its momentum is unknown.
      Any theoretical attempt at narrowing down the position (combining waves or ‘wave packets’) makes finding the wavelength more difficult and uncertain. In other words, if the electron is ‘part wave and part particle’ then we can only know ‘part momentum and part location’!

    • In 1926, the Schrodinger equation was developed to describe the wave behaviour of electrons over time using wave functions.

  • The most important point from the above is that drawing electrons as particles orbiting around a nucleus is WRONG. Showing electrons in shells ‘orbiting’ around the nucleus suggest they are single point charges (they aren’t) and we know exactly where they are (we don’t).
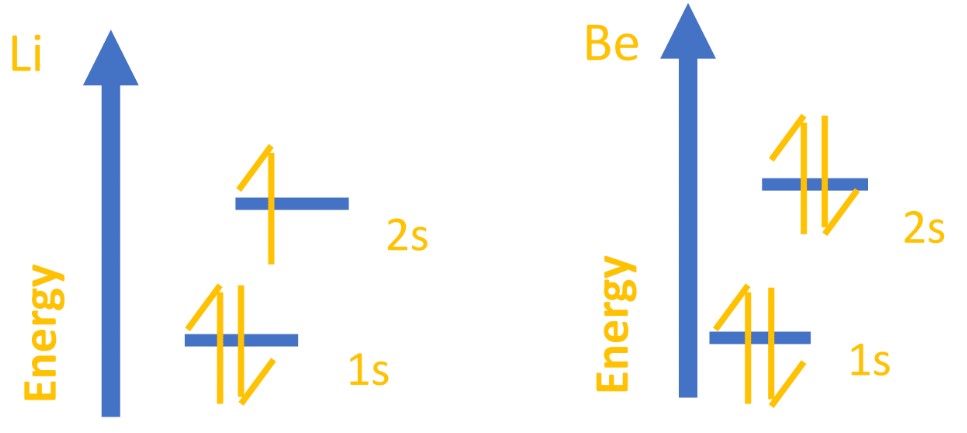
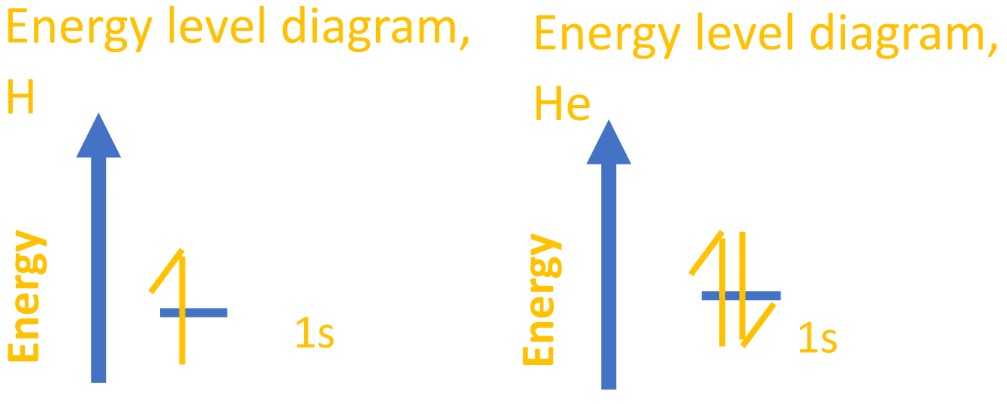
    Electrons are better thought of as ‘clouds’ of density inside orbitals where they are most likely to be found. Orbitals are like electron houses; they aren’t always/definitely there, but they are most likely there (or more likely there than anywhere else).

  • All orbitals can hold two electrons, no more. This is part of the Pauli principle. This first 1s orbital, then, covers the electrons for hydrogen and helium, which you can show using an energy-level diagram or subshell notation.

  • The first, lowest energy orbital is called a 1s orbital.
    • 1 refers to an energy level; the lower it is, the more stable it is and the closer to the nucleus it is.
    • S refers to shape – think s for sphere .
    The 1s orbital is spherical and covers the area closest to the positive nucleus. This is the lowest energy orbital because a negative electron will experience greatest attraction to a positive nucleus the closer it is. See below for the energy level diagrams for H and He.

    Atomic orbitals

  • After the first two electrons are filled in the 1s orbital, the third and fourth electrons are found in the 2s orbital. This is where the third electron of Li and third/fourth for Be are found.
    • Again, s means spherical but 2 shows a higher energy level. This orbital is higher in energy than 1s because the electrons are normally further away from the nucleus.
    The 2s orbital is different from 1s however, because it has a node. A node is an electron ‘dead zone’ - there is zero chance of the electron being found here.
    Because this zero node separates the orbital into two halves, it is convention to draw these halves as opposing regions (red/blue, +/-, shaded/unshaded). This is how we try and show the part wave nature of the electrons in orbitals:
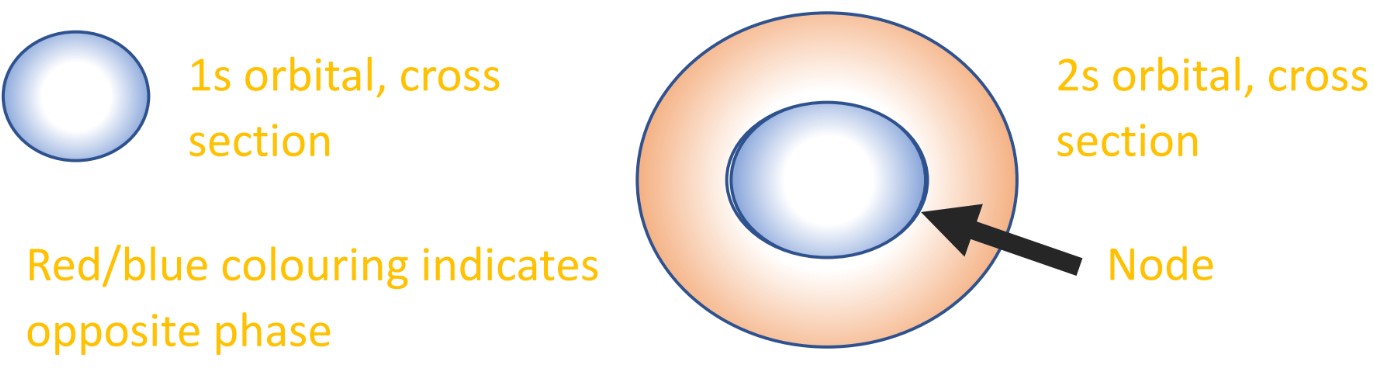
    • The positive region will, for example, overlap with positive parts of other orbitals (constructive interference).
    • The positive part will cancel out negative parts of other orbitals (destructive interference).
    The energy level diagrams of Li and Be, with their 1s and 2s subshells and their shapes are shown below:

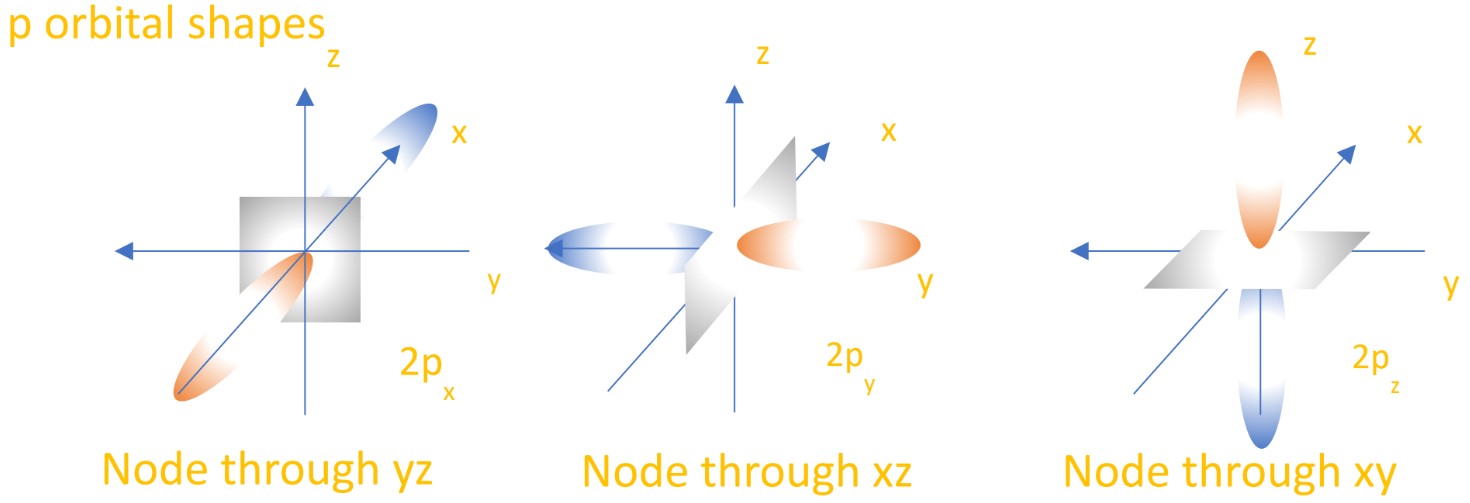
    Atomic orbitals
    Atomic orbitals


  • The 2nd energy level also has orbitals where the node is not spherical, but in a single plane. These are called p orbitals, and there are three in each energy level - one each for the x, y and z axes they occupy. They are considered “lobe shaped”. See below for images:

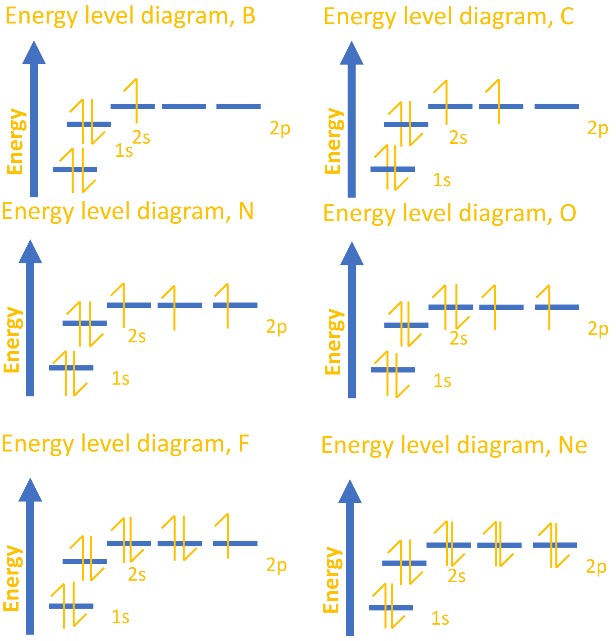
    • Atomic orbitals

  • With two electrons each, this gives the electron configurations for the elements boron through neon. See the diagram below for the energy level diagrams:

    • Atomic orbitals

  • The evidence for electron sublevels or subshells largely comes from photoelectron spectroscopy (PES), a development from the photoelectric effect. This is covered in our lesson Photoelectron spectroscopy.
Concept

Introduction to Atomic Orbitals and Energy Levels

Atomic orbitals and energy levels are fundamental concepts in understanding the structure of atoms and electron behavior. The introduction video provides a crucial foundation for grasping these complex ideas. Quantum theory revolutionized our understanding of atomic structure, revealing that electrons don't orbit the nucleus like planets around the sun, but exist in probability clouds called orbitals. These orbitals represent regions where electrons are likely to be found and are characterized by specific energy levels. The quantum mechanical model explains how electrons occupy these energy levels and transition between them, giving rise to atomic spectra and chemical properties. This understanding is essential for explaining chemical bonding, spectroscopy, and various phenomena in materials science. By delving into atomic orbitals and energy levels, we gain insight into the microscopic world that shapes the macroscopic properties of matter, highlighting the profound impact of quantum theory on our comprehension of nature at its most fundamental level.

Example

What are electron orbitals? What affects molecular/atomic properties?

Step 1: Introduction to Atomic Orbitals and Energy Levels

In this lesson, we will delve into the topic of atomic orbitals and energy levels. Depending on your prior knowledge or the sequence of lessons you have followed, you might already be familiar with atomic orbitals. This section serves as an introduction to the nature of atomic orbitals and the historical development of our understanding of them. The concept of what electrons are doing in atoms has evolved significantly since the first atomic models were proposed.

Step 2: Historical Development and Experimental Evidence

Our current understanding of atomic orbitals is based on a series of experimental evidence and theoretical developments. Initially, the models of the atom were quite different from what we understand today. Over time, through various experiments and observations, scientists have refined the model to include the concept of atomic orbitals. These orbitals help us understand the behavior of electrons in atoms and their role in chemical bonding.

Step 3: Shape and Nature of Electron Orbitals

Electron orbitals have specific shapes and energy levels. The lower energy electron orbitals have distinct shapes, which are crucial for understanding how electrons occupy these orbitals. The energy level diagrams help visualize the distribution of electrons in different orbitals. Understanding the shape and nature of these orbitals is essential for comprehending how atoms bond to form molecules.

Step 4: Filling Electron Orbitals

Filling electron orbitals follows specific rules and notations, such as subshell notation. This process determines the arrangement of electrons in an atom, which in turn affects the atom's chemical properties. The shape and nature of the orbitals play a significant role in this arrangement, influencing how atoms interact with each other.

Step 5: Role of Orbitals in Chemical Bonding

Orbitals are fundamental to understanding chemical bonding. They explain how atoms join together to form molecules. Various methods and theories have been developed to describe chemical bonding, with orbitals being a central concept. For example, the shape of molecules, such as the trigonal planar shape of borane (BH3) or the tetrahedral shape of methane (CH4), is determined by the arrangement of orbitals and the electrons within them.

Step 6: Influence of Electrons on Molecular Shape

The shape of a molecule is influenced by the electrons and their states. For instance, changing the central atom in a molecule can alter its shape due to the different electron configurations. The same number of electrons can result in different molecular shapes depending on the states of the electrons. This is evident in molecules like ammonia (NH3) and phosphine (PH3), where the arrangement of atoms is dictated by the electrons.

Step 7: Stability of Molecules and Atoms

The stability of molecules and atoms is also influenced by the electron configuration. For example, helium, with its two electrons, does not form stable molecules but is stable as an individual atom. The comparison of different atoms and molecules with the same number of electrons but different shapes highlights the role of electron states in determining molecular properties.

Step 8: Quantum Theory and Atomic Orbitals

Our understanding of atomic orbitals is rooted in quantum theory. This theory explains the behavior of electrons in atoms and how they occupy specific orbitals. The development of quantum theory and the experiments that led to the concept of orbitals are crucial for understanding the current model of the atom.

Step 9: Conclusion

In conclusion, atomic orbitals and energy levels are essential concepts for understanding the behavior of electrons in atoms and their role in chemical bonding. The shape and nature of orbitals, the arrangement of electrons, and the influence of electron states on molecular shape and stability are all critical factors that affect molecular and atomic properties. Our current understanding is based on a combination of experimental evidence and theoretical developments, particularly quantum theory.

FAQs

Here are some frequently asked questions about atomic orbitals and energy levels:

  1. What are the orbitals in order of energy level?

    The orbitals in order of increasing energy level are: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p. This order follows the Aufbau principle, which states that electrons fill orbitals from lowest to highest energy.

  2. What are the 4 types of orbitals?

    The four main types of orbitals are s, p, d, and f. Each type has a distinct shape: s orbitals are spherical, p orbitals are dumbbell-shaped, d orbitals have a clover-leaf shape, and f orbitals have more complex geometries.

  3. How are orbitals related to energy levels?

    Orbitals are directly related to energy levels. Each energy level (principal quantum number n) contains one or more sublevels (s, p, d, f), which in turn contain orbitals. As the energy level increases, so does the number of available sublevels and orbitals.

  4. Which orbital has the lowest energy?

    The 1s orbital has the lowest energy. This is because it is closest to the nucleus, where the electron experiences the strongest attractive force from the positively charged protons.

  5. How do you find the energy level of an orbital?

    The energy level of an orbital is determined by its principal quantum number (n). For example, in the notation 2p, the number 2 indicates the energy level. The letter (s, p, d, or f) represents the sublevel within that energy level.

Prerequisites

Understanding atomic orbitals and energy levels is a fundamental concept in chemistry and quantum mechanics. While there are no specific prerequisite topics provided for this subject, it's important to recognize that a strong foundation in basic chemistry and physics principles can greatly enhance your comprehension of this complex topic.

Atomic orbitals and energy levels are at the heart of our understanding of atomic structure and electron behavior. To fully grasp these concepts, students should have a solid understanding of basic atomic structure, including the components of atoms (protons, neutrons, and electrons) and their arrangement. Familiarity with the periodic table and electron configuration is also beneficial, as these provide context for how electrons are distributed in different elements.

Additionally, a basic understanding of quantum mechanics can be incredibly helpful when delving into atomic orbitals and energy levels. The wave-particle duality of electrons and the principles of quantum mechanics form the basis for our modern understanding of electron behavior in atoms. While not strictly prerequisites, these concepts are closely intertwined with the study of atomic orbitals and energy levels.

Mathematical skills, particularly in algebra and basic calculus, can also be valuable when exploring this topic. Many of the principles governing atomic orbitals and energy levels are expressed through mathematical equations and models. A comfort with mathematical concepts can make it easier to understand and apply these principles.

Furthermore, knowledge of spectroscopy and how atoms interact with light can provide practical applications and real-world context for the study of atomic orbitals and energy levels. Understanding how electrons transition between energy levels and emit or absorb specific wavelengths of light is crucial in many areas of chemistry and physics.

While these topics are not listed as formal prerequisites, having a strong background in general chemistry, basic physics, and introductory quantum mechanics can significantly enhance your ability to understand and appreciate the complexities of atomic orbitals and energy levels. As you explore this fascinating subject, you'll find that it builds upon and integrates many fundamental concepts from various areas of science.

Remember, learning is a journey, and it's okay if you don't have a perfect understanding of all these related topics. The study of atomic orbitals and energy levels itself will help reinforce and expand your knowledge in these areas. Approach the subject with curiosity and patience, and don't hesitate to review foundational concepts as needed. This approach will not only help you grasp atomic orbitals and energy levels more effectively but also deepen your overall understanding of chemistry and physics.