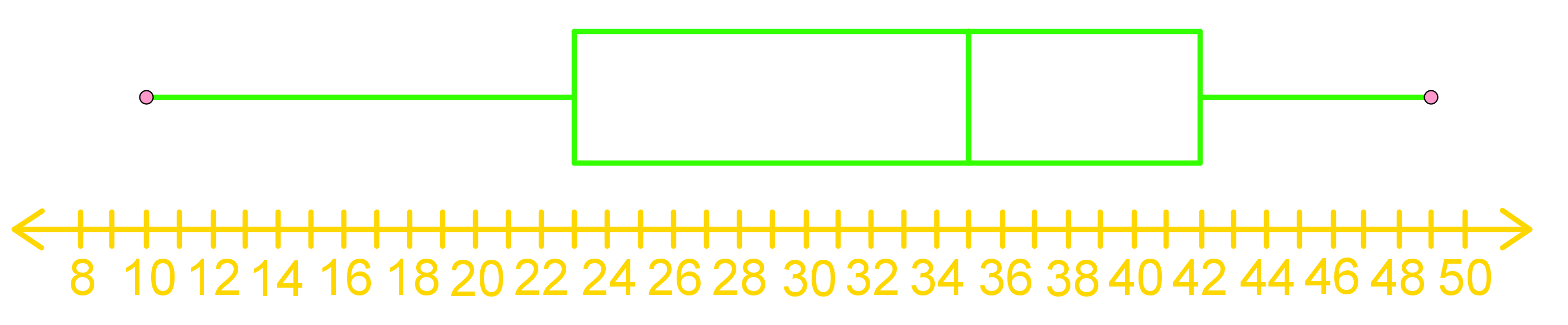Introduction
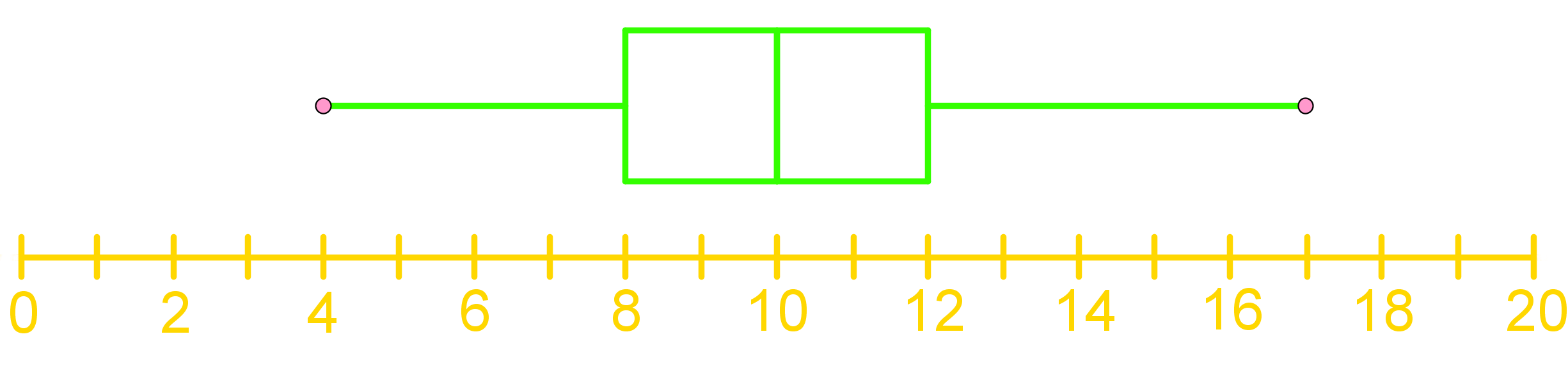
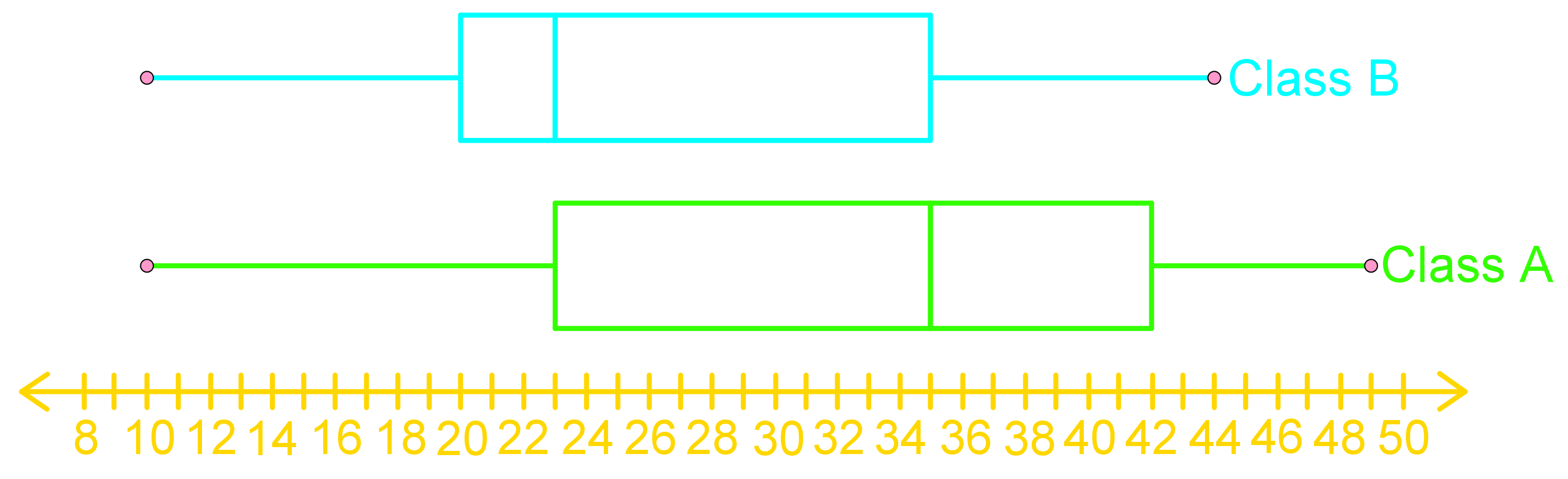
Box-and-whisker plots and scatter plots are essential statistical tools for data visualization and analysis. Box-and-whisker plots, also known as box plots, provide a concise summary of a dataset's distribution, displaying key statistics like median, quartiles, and outliers. Scatter plots, on the other hand, illustrate the relationship between two variables by plotting individual data points on a two-dimensional graph. The introduction video serves as a valuable resource for understanding these powerful visualization techniques. It demonstrates how to interpret and create both types of plots, highlighting their unique features and applications. By mastering these tools, analysts can quickly identify patterns, trends, and anomalies in complex datasets. Box-and-whisker plots excel at comparing distributions across multiple groups, while scatter plots are ideal for exploring correlations and identifying clusters. Together, these plots form a fundamental part of any data scientist's toolkit, enabling more informed decision-making and deeper insights into various phenomena across diverse fields of study.