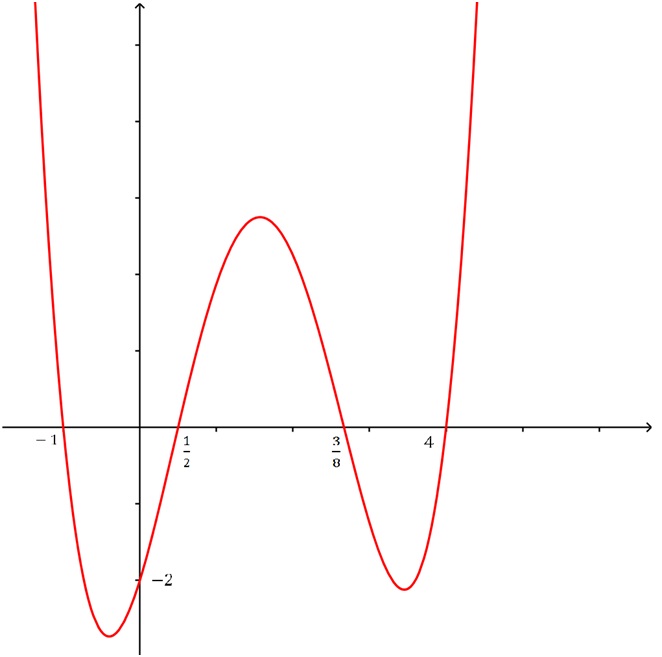
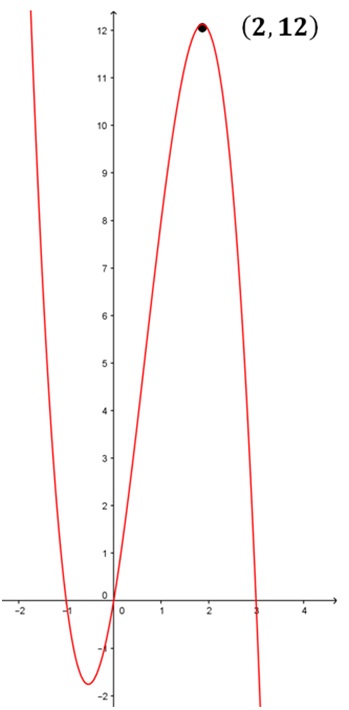
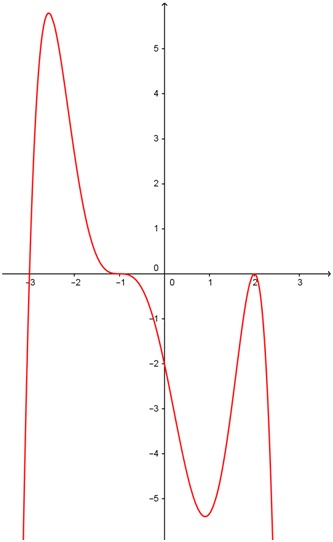
1. Find the zeros, write them out in factored form.
2. Determine the multiplicity each zero by observing the behavior of the graph near the zero.
3. Determine the leading coefficient C by plugging in the coordinates of a point (other than the x-intercepts) on the graph.