How to find the surface area of a pyramid
The surface area of a shape tell us the areas of all the different sides of the shape summed together. In this chapter, we're learning about the surface area and volumes of pyramids. There's many different pyramids such as a square pyramid or a rectangular pyramid. So how do we find the surface area of a pyramid? There are actually formulas to help you find this.
Surface area formula
For a general right pyramid whose faces are all the same, the surface area = the sum of all the areas of the pyramid's faces.
For a square-based pyramid, you'll need to calculate the area of the triangle using: (for each triangle that you're working with), then find the area of the base. This means your formula will be
Essentially, for both of these formulas, you're just finding all the areas of the different sides of a pyramid and then adding it together to get the total surface area. You can imagine the net of a 3D shape spread out, and having to calculate each of the sections of the net's area separately.
how to find the volume of a pyramid
The volume tells you how much space an object takes up. For a pyramid, you can use the below formula to help you find the answer.
Formula for volume
Volume of a pyramid = x (area of base) x
Examples problems
Question:
Find the surface area and the volume
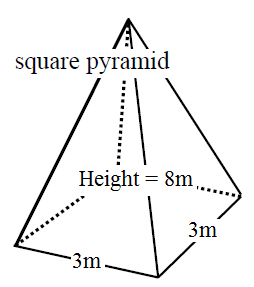
Solution:
First, we are looking for the surface area (SA). We will have to look for the area of the base and the four triangular sides. For the triangular sides, we are missing the height of the triangle. So, let's first look for the height. We can do this with the help of the pythagorean theorem:
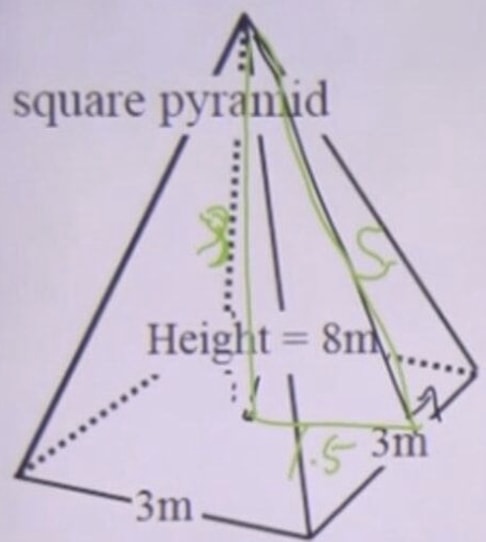
Area of a triangular side:
There are four sides, so:
Now look for the area of the base:
Area of base =
Add the triangular sides and base together:
SA =
Now, look for the volume of a square pyramid:
Question 2:
Find the surface area and the volume
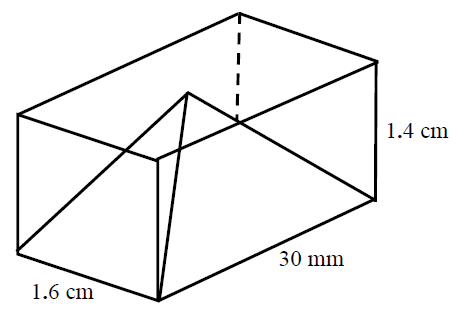
Solution:
We're going to start with looking for the Surface area(SA). Before that, we need to convert unequal units and gather the required information that are not given to us in the graph.
First, we want all numbers in centimeter. So,
Then, we need to look for the height of the triangular sides. We have two triangles in different sizes. So we need to look for and . From the graph, we have the following information
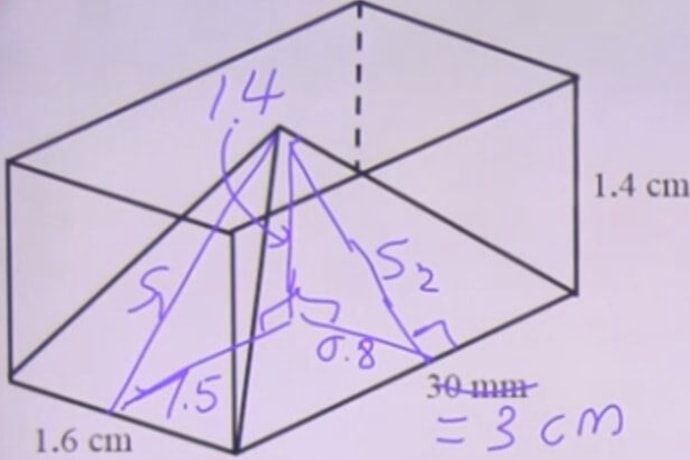
Now, calculate
Now, calculate
Now, look for the surface area
SA of base = =
Look for the area of the sides. We have sides with different sizes. Sides on left and right are identical to each other. It's the same for sides on the front and the back.
Now, calculate the front and back
Now, calculate the left and right
Add the triangular sides and base together:
Now, look for the volume:
Feel free to explore the volume of a triangular pyramid further with this online volume calculator. If you're ready to move on, learn about the surface area and volume of other shapes and try out some volume word problems.








