ellipse: the sum of the distances from any point on an ellipse to each focus is constant and equal to the major axis .
: distance from the center to a focus
: eccentricity; the larger the value of , the straighter the hyperbola
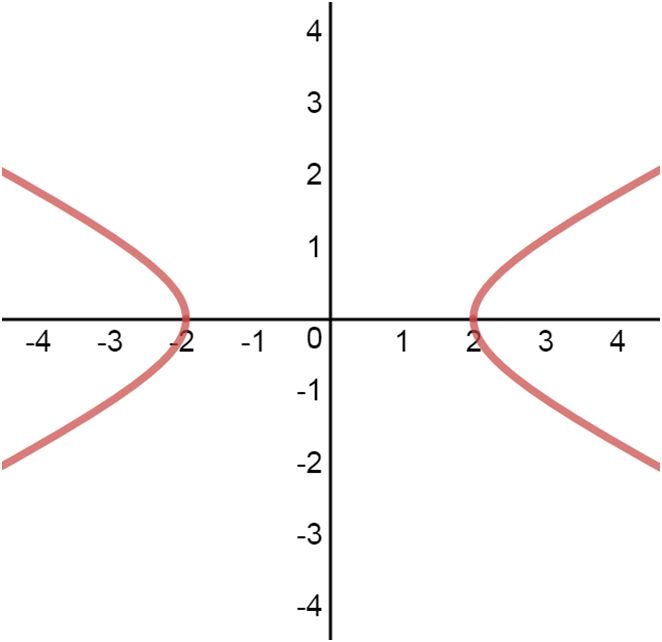 vertical hyperbola
vertical hyperbola



Welcome to the fascinating world of hyperbolas! Our introduction video serves as an essential starting point for understanding these intriguing conic sections. Hyperbolas are unique curves with two distinct branches that extend infinitely, creating a captivating visual representation in mathematics. The video provides a comprehensive overview, offering students a solid foundation to grasp the concept of hyperbola graphs. By watching this introductory content, you'll gain insights into the basic shape, key components, and general behavior of hyperbolas. The video's significance lies in its ability to simplify complex mathematical concepts, making them more accessible to learners. As you begin your journey into the realm of hyperbolas, this visual guide will help you visualize the curves and understand their fundamental properties. Remember, while the video gives a rough idea of hyperbola graphs, it's an excellent springboard for deeper exploration and understanding of these remarkable mathematical entities.
properties of a hyperbola
−(4x−6)2+(3y+5)2=1
Identify the type of conic section.
We are given the equation −(4x−6)2+(3y+5)2=1. This is the equation we need to analyze to determine the type of conic section it represents.
First, let's identify whether the variables x and y are squared. In this equation, both x and y are squared. This is evident from the terms (4x−6)2 and (3y+5)2.
To determine if the equation represents a parabola, we need to check if only one of the variables is squared. In this case, both x and y are squared, so this equation does not represent a parabola.
Next, we need to check if the equation could represent an ellipse or a circle. For an equation to represent an ellipse or a circle, two conditions must be met:
Since the equation does not represent a parabola, ellipse, or circle, the remaining option is a hyperbola. For an equation to represent a hyperbola, two conditions must be met:
Based on the analysis, we can conclude that the given equation −(4x−6)2+(3y+5)2=1 represents a hyperbola. This conclusion is drawn from the fact that both variables are squared and the squared terms have opposite signs.
A hyperbola is a type of conic section that consists of two open curves, called branches, which are mirror images of each other. It is formed when a plane intersects both nappes of a double cone. Hyperbolas have unique properties, including two focal points and asymptotes that the curves approach but never touch.
Horizontal hyperbolas open left and right, with their transverse axis parallel to the x-axis. Their standard form equation is (x²/a²) - (y²/b²) = 1. Vertical hyperbolas open up and down, with their transverse axis parallel to the y-axis. Their standard form equation is (y²/a²) - (x²/b²) = 1. The orientation affects the placement of vertices and foci.
The key components of a hyperbola include: center (the midpoint between vertices), vertices (points where the hyperbola intersects its transverse axis), foci (two fixed points that define the hyperbola), transverse axis (the line segment connecting the vertices), conjugate axis (perpendicular to the transverse axis), and asymptotes (lines that the hyperbola approaches but never touches).
To find the foci, use the formula c² = a² + b², where 'a' is the distance from the center to a vertex, and 'b' is half the length of the conjugate axis. Calculate 'c', then for a horizontal hyperbola with center (h,k), the foci are at (h±c, k). For a vertical hyperbola, they're at (h, k±c).
Hyperbolas have various real-world applications, including: modeling the paths of comets and other celestial bodies in astronomy, designing satellite dishes and radio telescopes for optimal signal reception, calculating sound wave trajectories in acoustics, and describing cooling tower shapes in architecture and engineering. They're also used in navigation systems and in studying relativistic physics.
Understanding the foundations of mathematics is crucial when delving into more advanced concepts like Conics - Hyperbola. One of the most essential prerequisite topics for mastering hyperbolas is graphing from slope-intercept form y=mx+b. This fundamental skill serves as a stepping stone to comprehending the more complex equations and graphical representations associated with hyperbolas.
The ability to graph linear functions using various forms, particularly the slope-intercept form, provides students with a solid foundation for visualizing mathematical relationships on a coordinate plane. This skill is directly applicable when working with hyperbolas, as it helps in understanding how changes in equation parameters affect the shape and position of the curve.
When studying hyperbolas, students encounter the standard form equation, which is more intricate than the linear equations they've previously worked with. However, the principles learned from graphing linear functions remain relevant. For instance, the concept of intercepts, which is crucial in slope-intercept form, also plays a significant role in determining key points of a hyperbola.
Moreover, the slope in linear equations relates to the rate of change, which is analogous to the steepness of the hyperbola's asymptotes. Understanding how to manipulate the 'm' and 'b' values in y=mx+b prepares students for working with the more complex parameters in the hyperbola equation standard form.
As students progress from linear functions to conics, they build upon their existing knowledge. The skills developed in graphing linear equations, such as plotting points, identifying x and y intercepts, and recognizing the impact of coefficients on the graph, are all transferable to the study of hyperbolas. This continuity in mathematical concepts helps students make connections and grasp new ideas more effectively.
Furthermore, the confidence gained from mastering linear graphing techniques provides a strong foundation for tackling the challenges presented by hyperbolas. Students who are proficient in graphing from slope-intercept form are better equipped to visualize and interpret the more complex conic sections, including hyperbolas.
In conclusion, the journey from basic linear equations to the intricacies of hyperbolas is a natural progression in mathematics. By thoroughly understanding prerequisite topics like graphing linear functions, students develop the necessary skills and intuition to explore more advanced concepts with confidence. This solid foundation not only facilitates learning about hyperbolas but also enhances overall mathematical proficiency and problem-solving abilities.
