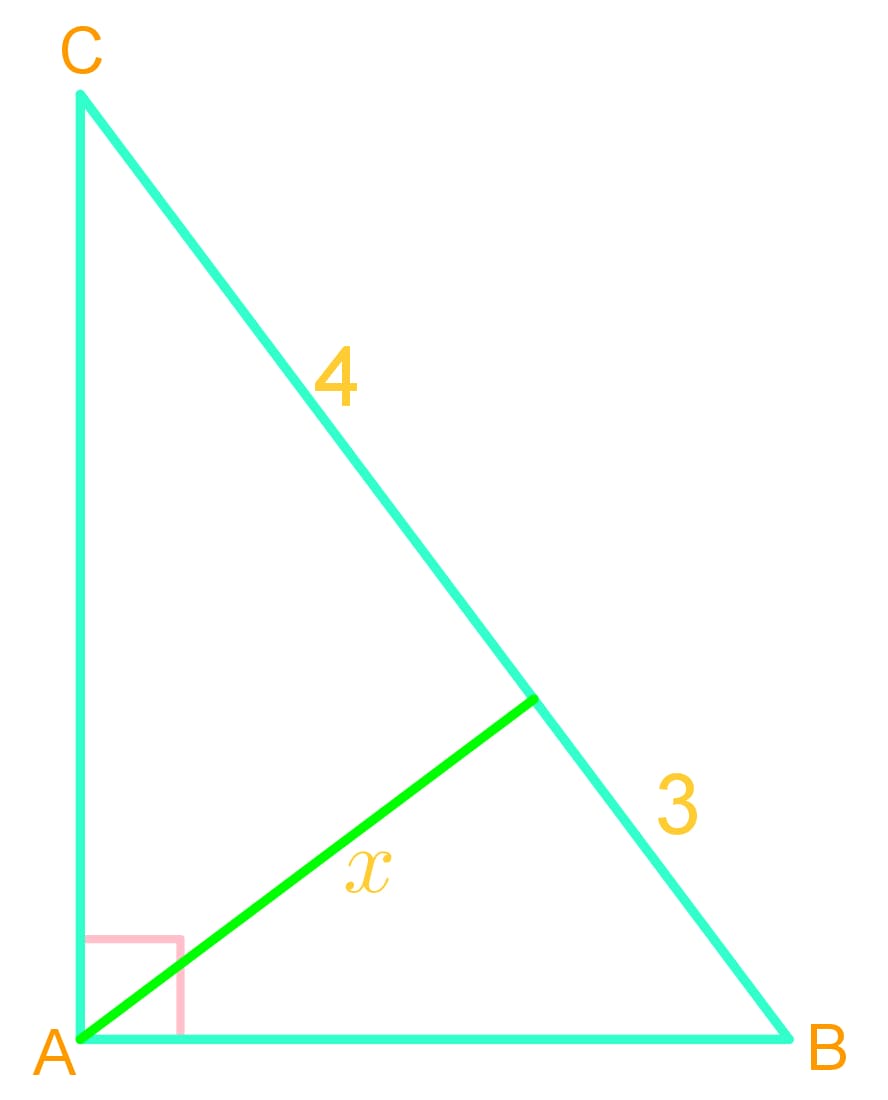
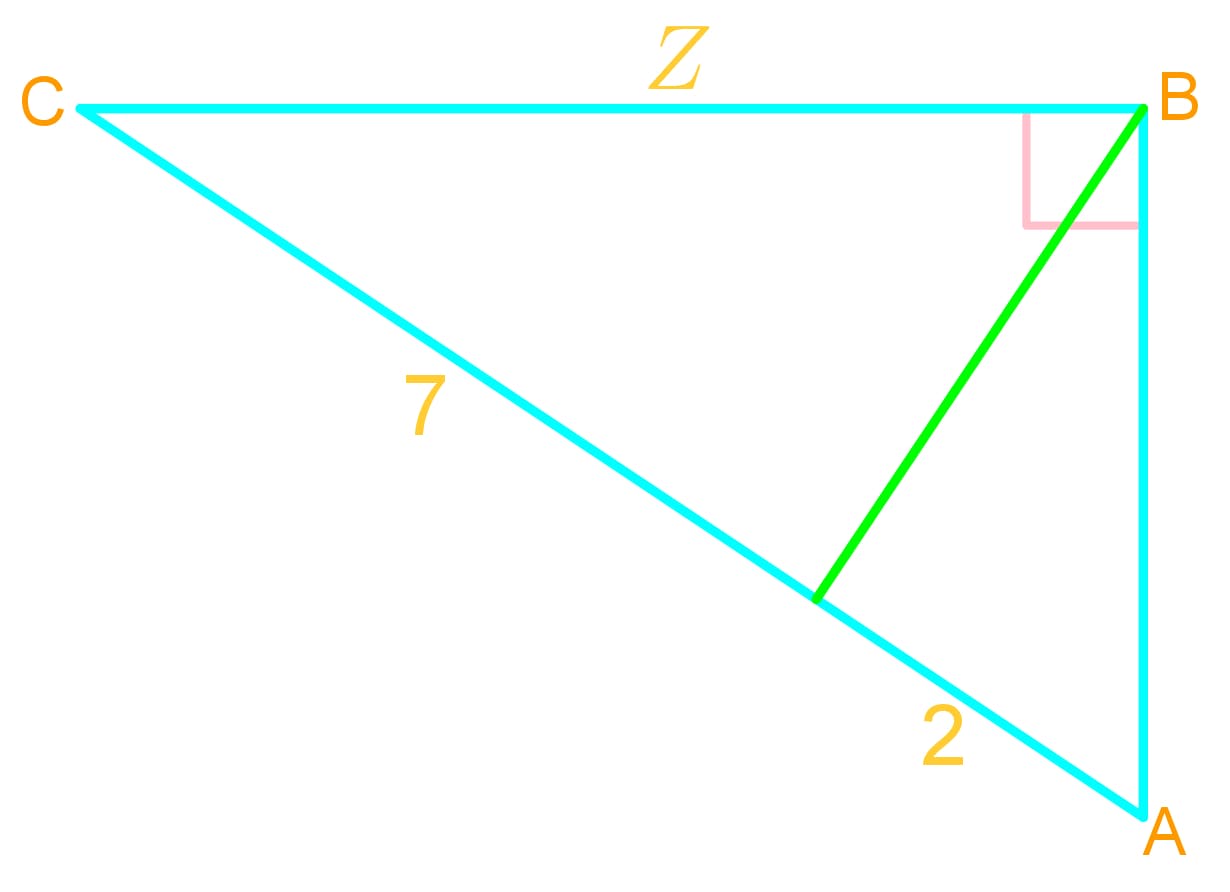
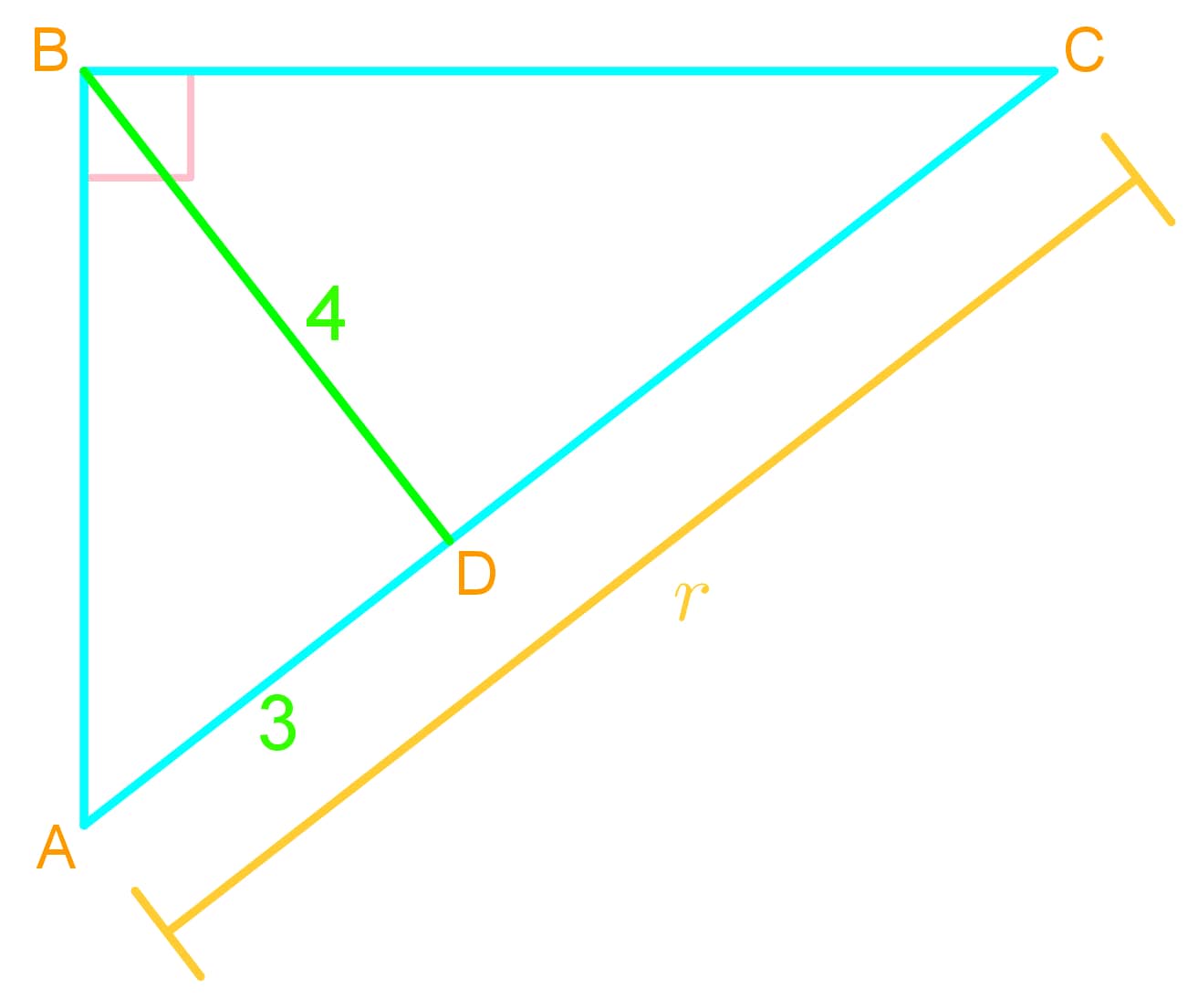
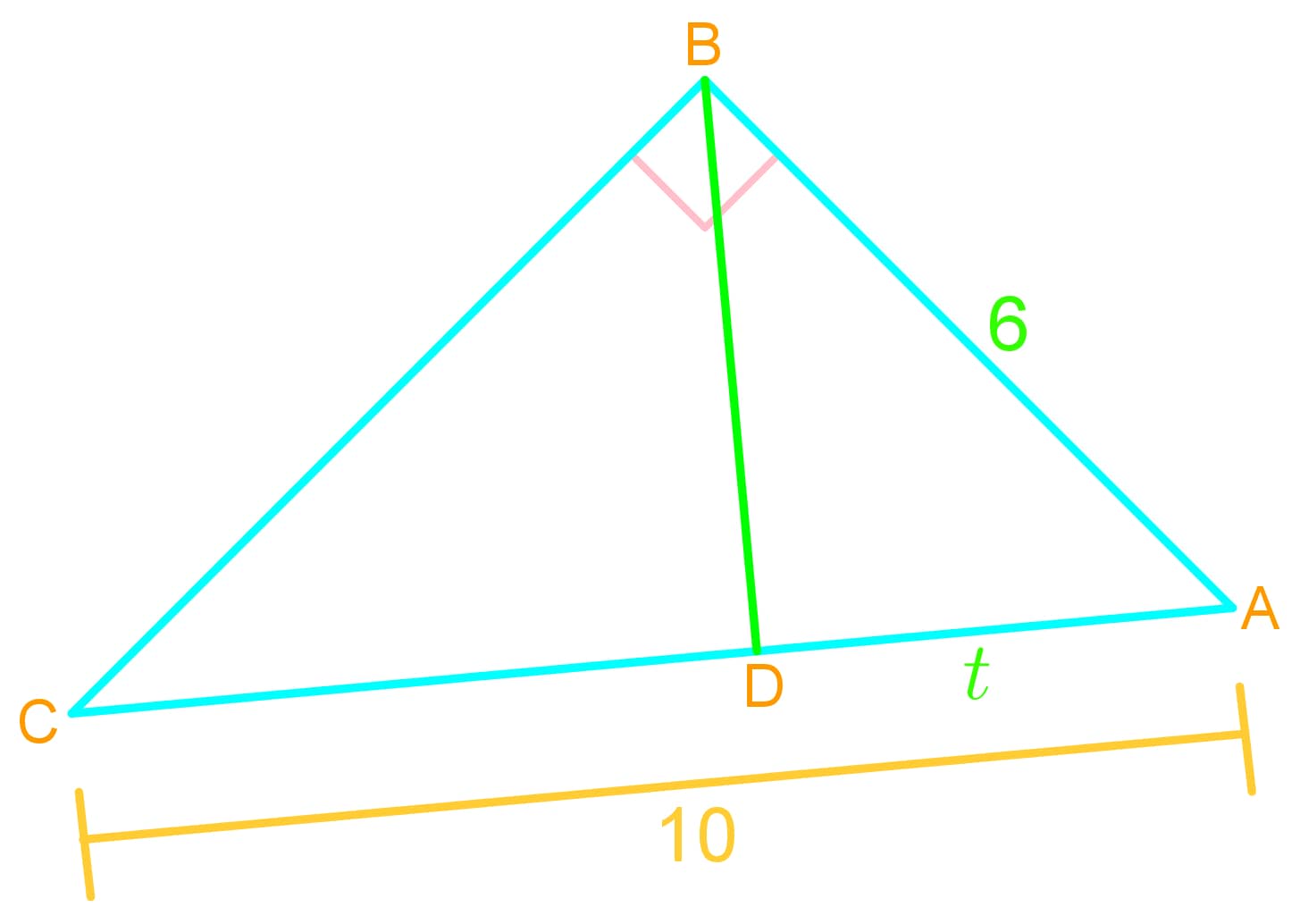
Introduction to Arithmetic and Geometric Means
Welcome to our exploration of arithmetic and geometric means! These fundamental concepts in mathematics are essential for understanding data analysis and statistics. The arithmetic mean, often simply called the average, is calculated by summing up all values and dividing by the number of items. It's widely used in everyday situations, from calculating test scores to estimating typical temperatures. On the other hand, the geometric mean is less common but equally important, especially when dealing with growth rates or ratios. It's found by multiplying all values and then taking the nth root, where n is the number of items. Our introduction video provides a clear, visual explanation of both concepts, making them easy to grasp. As your virtual math tutor, I'm excited to guide you through these ideas, showing how they apply to real-world scenarios. Understanding these means will enhance your mathematical toolkit and problem-solving abilities. Let's dive in and unravel the mysteries of arithmetic and geometric means together!