Sign In
Try for free
flag-nz

Unlock the Power of Sequences in Mathematics
Dive into the world of sequences, from basic definitions to advanced concepts. Master notation, limits, and key theorems. Apply your knowledge to solve complex problems and understand real-world patterns.

  1. Intros0/2 watched
  2. Examples0/9 watched
  1. 0/2
  2. 0/9
Now Playing:Introduction to sequences – Example 0a
Intros
0/2 watched
  1. Overview:
  2. Notation of Sequences
  3. Definitions and theorems of Sequences
Examples
0/9 watched
  1. Finding the terms of a sequence

    Find the first five terms of the following sequences.
    1. an=3(−1)n a_n=3(-1)^n

    2. ana_n= n+1n+1\frac{n+1}{\sqrt{n+1}}

    3. {cos(nπ2) cos(\frac{n\pi}{2}) }

Introduction to sequences
Jump to:NotesConceptFAQsPrerequisitesRelated
Notes
In this lesson, we will talk about what sequences are and how to formally write them. Then we will learn how to write the terms out of the sequences when given the general term. We will also learn how to write the general term when given a sequence. After learning the notations of sequences, we will take a look at the limits of sequences. Then we will take a look at some definitions and properties which will help us take the limits of complicating sequences. These theorems include the squeeze theorem, absolute value sequences, and geometric sequences.
Note:
1. If a sequence has the limit LL, then we can say that:

lim⁡\limn →∞\infty aann=L=L

If the limit is finite, then it is convergent. Otherwise, it is divergent.

2. If the limit of the sequences {ana_n} and {bnb_n} are finite and cc is constant, then we can say that

i) lim⁡\limn →∞\infty (an+bn)=lim⁡(a_n+b_n)=\limn →∞\infty an+a_n+lim⁡\limn →∞\infty bnb_n.
ii) lim⁡\limn →∞\infty (an−bn)=lim⁡(a_n-b_n)=\limn →∞\infty an−a_n-lim⁡\limn →∞\infty bnb_n.
iii) lim⁡\limn →∞\infty can=cca_n=c lim⁡\limn →∞\infty ana_n.
iv) lim⁡\limn →∞\infty(anbn)=(a_nb_n)= lim⁡\limn →∞\inftyan∗a_n* lim⁡\limn →∞\infty bnb_n.
v) lim⁡\limn →∞\infty [an[a_n÷\divbn]b_n] =lim⁡=\limn →∞\inftyana_n÷\div lim⁡\limn →∞\inftybnb_n,, bn≠0b_n\neq0.

3. If an≤cn≤bna_n\leq c_n\leq b_n and lim⁡\limn →∞\infty an=a_n= lim⁡\limn →∞\infty bn=Lb_n=L, then lim⁡\limn →∞\infty cn=Lc_n=L.

4.if lim⁡\limn →∞\infty ∣an∣=0|a_n|=0, then lim⁡\limn →∞\infty an=0a_n=0 as well.

5. We say that:

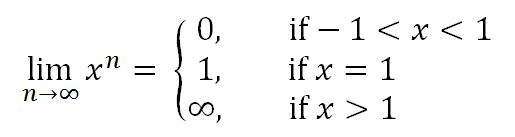
Introduction to sequences

Where the sequence {xnx^n} is convergent for -1< x≤x \leq 1, and divergent if xx > 1.
Concept

Introduction to Sequences

Welcome to our exploration of sequences, a fundamental concept in mathematics. Our journey begins with an engaging introduction video that sets the stage for understanding these fascinating mathematical patterns. Sequences are ordered lists of numbers that follow specific rules, and they play a crucial role in various mathematical applications. In this lesson, we'll delve into the notation of sequences, providing you with the tools to read and interpret them effectively. We'll also cover the formal definition of sequences, ensuring a solid foundation for future studies. You'll learn how to write individual terms and develop general formulas for sequences, skills that are essential for solving complex mathematical problems. Understanding sequences is vital as they form the basis for many advanced mathematical concepts and real-world applications. By mastering sequences, you'll enhance your problem-solving abilities and gain insights into the beautiful patterns that underlie mathematics.

FAQs

Here are some frequently asked questions about sequences:

1. What is the difference between an arithmetic and a geometric sequence?

An arithmetic sequence has a constant difference between consecutive terms, while a geometric sequence has a constant ratio between consecutive terms. For example, 2, 5, 8, 11 is arithmetic (common difference of 3), and 2, 6, 18, 54 is geometric (common ratio of 3).

2. How do you find the nth term of an arithmetic sequence?

The nth term of an arithmetic sequence is given by the formula an = a1 + (n - 1)d, where a1 is the first term, n is the position of the term, and d is the common difference.

3. What is a convergent sequence?

A convergent sequence is one where the terms approach a specific finite value (called the limit) as the number of terms increases indefinitely. For example, the sequence 1/n converges to 0 as n approaches infinity.

4. How can the squeeze theorem be used to find sequence limits?

The squeeze theorem states that if an bn cn for all n greater than some value, and if lim(an) = lim(cn) = L, then lim(bn) must also equal L. This is useful for finding limits of complex sequences by "sandwiching" them between simpler sequences.

5. What is the limit of the sequence (1 + 1/n)n as n approaches infinity?

The limit of the sequence (1 + 1/n)n as n approaches infinity is the mathematical constant e, approximately equal to 2.71828. This sequence is important in calculus and is often used to define the number e.

Prerequisites

Before diving into the fascinating world of sequences, it's crucial to have a solid foundation in certain mathematical concepts. One of the most important prerequisite topics for understanding sequences is the Squeeze theorem. This fundamental principle plays a significant role in analyzing and determining the behavior of sequences, making it an essential tool in your mathematical toolkit.

The Squeeze theorem, also known as the sandwich theorem or pinching theorem, is a powerful concept that helps us determine the limit of a sequence by comparing it to two other sequences. This theorem is particularly useful when dealing with complex sequences where direct calculation of the limit might be challenging or impossible.

Understanding the Squeeze theorem for sequences provides a strong foundation for grasping more advanced concepts in sequence analysis. It allows you to approach problems from different angles and often simplifies the process of finding limits. This theorem is not only applicable to sequences but also extends to functions and series, making it a versatile tool in calculus and mathematical analysis.

When studying sequences, you'll frequently encounter situations where the behavior of a sequence is not immediately apparent. The Squeeze theorem comes to the rescue in such scenarios, allowing you to bound the sequence between two simpler sequences whose limits are known or easier to calculate. This approach is particularly valuable when dealing with oscillating or irregularly behaving sequences.

Moreover, the Squeeze theorem helps develop critical thinking and problem-solving skills. It encourages you to think creatively about how to bound a sequence and identify appropriate comparison sequences. These skills are invaluable not only in studying sequences but also in tackling more advanced mathematical concepts and real-world applications.

As you progress in your study of sequences, you'll find that the Squeeze theorem becomes an indispensable tool. It will help you in proving convergence, finding limits, and understanding the behavior of complex sequences. The theorem's applications extend beyond just sequences, making it a fundamental concept in calculus and mathematical analysis.

By mastering the Squeeze theorem, you'll be well-prepared to tackle more advanced topics in sequence analysis. It will provide you with a solid foundation for understanding convergence, divergence, and the limiting behavior of sequences. This knowledge will prove invaluable as you delve deeper into the study of series, infinite sums, and other advanced mathematical concepts.

In conclusion, a thorough understanding of the Squeeze theorem is essential for anyone looking to master the intricacies of sequences. It serves as a bridge between basic algebraic concepts and more advanced calculus topics, making it an indispensable prerequisite for your journey into the world of sequences and beyond.