Sign In
Sign Up
flag-us

Chain Rule for Multivariable Functions: Unlocking Complex Derivatives
Discover how to tackle complex derivatives with the chain rule for multivariable functions. Master this essential calculus concept through clear explanations, step-by-step examples, and practical applications.

  1. Intros0/4 watched
  2. Examples0/6 watched
  1. 0/4
  2. 0/6
Now Playing:Chain rule for multivariable functions – Example 0a
Intros
0/4 watched
  1. Chain Rule for Multivariable Functions Overview:
  2. Chain Rule for Multivariable Functions Overview:
    A Review of Chain Rule
    • What is the chain rule?
    • h(x)=f(g(x))→h′=f′(g(x))g′(x)h(x)=f(g(x))\to h' =f'(g(x))g'(x)
    • alternate notation: dtdt=dfdxdxdt\frac{dt}{dt} = \frac{df}{dx} \frac{dx}{dt}
  3. Chain Rule for Multivariable Functions Overview:
    1st Case of Chain Rule for 2 Variable Functions
    • z=f(x,y),x=g(t),y=h(t)z=f(x,y), x=g(t), y=h(t)
    • Then dzdt=dfdxdxdt+dfdydydt \frac{dz}{dt} = \frac{df}{dx} \frac{dx}{dt} + \frac{df}{dy} \frac{dy}{dt}
    • An example
Examples
0/6 watched
  1. Finding the Chain Rule for 2 Variable Functions
    Given that z=sin⁡(xy),x=t3,y=1−tz=\sin (xy), x= t^3, y=1-t, find dzdt \frac{dz}{dt} .
    Functions of several variables
    Jump to:NotesConceptExampleFAQsPrerequisites
    Notes
    Notes:


    Suppose we have a function y=f(g(x))y=f(g(x)). Then the chain rule is:

    y =f′(g(x))g′(x)y\ = f'(g(x))g'(x)

    We can rewrite this using an alternate notation:

    dydx=dfdgdgdx \frac{dy}{dx} = \frac{df}{dg} \frac{dg}{dx}

    Now if we were to change g→xg \to x and x→tx\to t, then we have the chain rule to be:

    dydt=dfdxdxdt\frac{dy}{dt} = \frac{df}{dx} \frac{dx}{dt}

    Why do we want this alternate notation? Because it relates to the chain rule for 2 variable functions.

    1st Case of Chain Rule for 2 Variable Functions
    Suppose we have z=f(x,y)z=f(x,y), x=g(t)x=g(t), and y=h(t)y=h(t), then the chain rule (derivative of zz in respect to tt) is:

    dzdt=dfdxdxdt+dfdydydt\frac{dz}{dt} = \frac{df}{dx} \frac{dx}{dt} + \frac{df}{dy} \frac{dy}{dt}


    2nd Case of Chain Rule for 2 Variable Functions
    Suppose we have z=f(x,y)z=f(x,y),x=g(s,t) x=g(s, t),y=h(s,t) y=h(s, t), then there are 2 chain rules.
    The derivative of zz in respect to ss is:

    dzdx=dfdxdxdx+dfdydyds\frac{dz}{dx} = \frac{df}{dx} \frac{dx}{dx} + \frac{df}{dy} \frac{dy}{ds}

    The derivative of zz in respect to tt is:

    dzdt=dfdxdxdt+dfdydydt \frac{dz}{dt} = \frac{df}{dx} \frac{dx}{dt} + \frac{df}{dy} \frac{dy}{dt}


    Using a Tree Diagram for Chain Rule
    Tree diagrams are very useful when finding the chain rule for multivariable functions with more than 2 variables.
    For example, suppose we have w=f(x,y,z),x=g(s,t,r),y=h(s,t,r)w=f(x,y,z), x=g(s,t,r), y=h(s,t,r) and z=i(s,t,r)z=i(s,t,r), and we want to find dwdt\frac{dw}{dt}.
    We can write the tree diagram below like this:
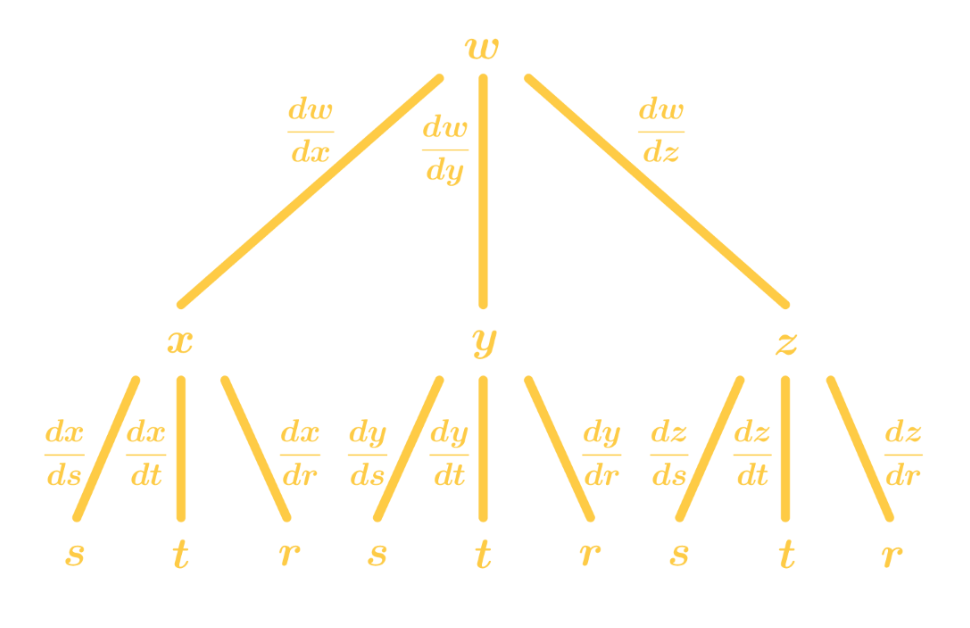
    chain rule tree diagram
    Then we will multiply all the connected derivatives, and sum them up to have:

    dwdt=dfdxdxdt+dfdydydt+dfdzdzdt\frac{dw}{dt} = \frac{df}{dx} \frac{dx}{dt} + \frac{df}{dy} \frac{dy}{dt} + \frac{df}{dz} \frac{dz}{dt}

    Concept

    Introduction to Chain Rule for Multivariable Functions

    The chain rule for multivariable functions is a fundamental concept in calculus that extends the single-variable chain rule to functions of multiple variables. This powerful tool is essential for solving complex problems in multivariable calculus. The introduction video provides a clear and concise explanation of this concept, making it an invaluable resource for students transitioning from single-variable to multivariable calculus. Understanding the chain rule for multivariable functions allows us to compute derivatives of composite functions involving multiple variables. It builds upon the foundation laid in single-variable calculus, introducing new notation and techniques specific to multivariable scenarios. By mastering this concept, students can tackle more advanced topics in calculus and apply their knowledge to real-world problems in physics, engineering, and economics. The chain rule for multivariable functions is a crucial stepping stone in developing a deeper understanding of calculus and its applications across various fields of study.

    Example

    Chain Rule for Multivariable Functions Overview: A Review of Chain Rule

    • What is the chain rule?
    • h(x)=f(g(x))→h′=f′(g(x))g′(x)h(x)=f(g(x))\to h' =f'(g(x))g'(x)
    • alternate notation: dtdt=dfdxdxdt\frac{dt}{dt} = \frac{df}{dx} \frac{dx}{dt}

    Step 1: Introduction to the Chain Rule

    Welcome to this section. Today, we are going to learn about the chain rule for multivariable functions. Before diving into the multivariable aspect, let's review the chain rule as it is used in single-variable calculus. The chain rule is a fundamental tool in calculus used to differentiate composite functions. In simpler terms, it helps us find the derivative of a function that is nested within another function.

    Step 2: Understanding the Basic Chain Rule

    In Calculus 1, the chain rule is applied when you have a function like y=f(g(x)) y = f(g(x)) . This is a function within a function, and the chain rule helps us differentiate it. The formula for the chain rule in this context is y′=dydx=f′(g(x))⋅g′(x) y' = \frac{dy}{dx} = f'(g(x)) \cdot g'(x) . This means that to find the derivative of y y with respect to x x , you first take the derivative of the outer function f f evaluated at the inner function g(x) g(x) , and then multiply it by the derivative of the inner function g(x) g(x) .

    Step 3: Alternate Notation for the Chain Rule

    There is also an alternate notation for the chain rule, which can sometimes make the concept clearer. This notation is written as dydx=dfdg⋅dgdx \frac{dy}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx} . Here, dfdg \frac{df}{dg} represents the derivative of the outer function f f with respect to the inner function g g , and dgdx \frac{dg}{dx} represents the derivative of the inner function g g with respect to x x . This notation emphasizes the idea that we are chaining together the derivatives of the nested functions.

    Step 4: Changing Variables in the Chain Rule

    To further illustrate the chain rule, let's change the variables in our notation. Suppose we replace all instances of g g with x x and all instances of x x with t t . This gives us a new form of the chain rule: dydt=dfdx⋅dxdt \frac{dy}{dt} = \frac{df}{dx} \cdot \frac{dx}{dt} . This notation is particularly useful when dealing with problems where the variables are not just x x and y y , but other variables like t t as well.

    Step 5: Importance of Alternate Notation

    Why do we use this alternate notation? The reason is that it helps us understand the chain rule in the context of multivariable functions. When dealing with multivariable functions, the chain rule becomes more complex, and this alternate notation provides a clearer framework for understanding how the derivatives of the nested functions interact with each other. This sets the stage for extending the chain rule to functions of multiple variables.

    Step 6: Transition to Multivariable Functions

    Now that we have a solid understanding of the chain rule for single-variable functions, we can transition to the chain rule for multivariable functions. The principles remain the same, but the application becomes more intricate as we deal with functions of several variables. In the next section, we will explore how the chain rule is applied in the context of multivariable calculus, providing a comprehensive understanding of this essential mathematical tool.

    FAQs

    1. What is the chain rule for multivariable functions?

      The chain rule for multivariable functions is a method for finding the derivative of composite functions involving multiple variables. It extends the single-variable chain rule to more complex scenarios. For a function z = f(x, y) where x and y are functions of t, the chain rule states that dz/dt = (f/x)(dx/dt) + (f/y)(dy/dt).

    2. How does the chain rule differ for two-variable functions in Case 1 and Case 2?

      In Case 1, we have z = f(x,y) where x and y are functions of a single variable t. The formula is dz/dt = (f/x)(dx/dt) + (f/y)(dy/dt). In Case 2, x and y are functions of two variables s and t. The formulas are z/s = (f/x)(x/s) + (f/y)(y/s) and z/t = (f/x)(x/t) + (f/y)(y/t).

    3. How can tree diagrams help in solving complex chain rule problems?

      Tree diagrams provide a visual representation of the relationships between variables in complex functions. They help organize the problem, making it easier to identify the correct partial derivatives and their order of multiplication. Each path in the tree corresponds to a term in the chain rule formula, simplifying the process of deriving and applying the rule.

    4. What are some real-world applications of the multivariable chain rule?

      The multivariable chain rule has numerous applications in physics, engineering, and economics. It's used in thermodynamics to calculate rates of change in complex systems, in fluid dynamics to analyze flow rates, and in economics to study the relationships between multiple economic variables. It's also crucial in optimization problems involving multiple variables.

    5. How does the multivariable chain rule relate to partial derivatives?

      The multivariable chain rule combines partial derivatives to find the total derivative of a composite function. It uses partial derivatives of the outer function with respect to each of its variables, multiplied by the derivatives of those variables with respect to the independent variable(s). This allows us to account for how changes in each variable contribute to the overall rate of change of the function.

    Prerequisites

    Understanding the chain rule for multivariable functions is a crucial concept in advanced calculus, but it's essential to have a solid foundation in several prerequisite topics. These fundamental concepts provide the necessary groundwork for grasping the complexities of multivariable calculus.

    One of the most important prerequisites is the single-variable chain rule. This concept serves as the building block for understanding its multivariable counterpart. The single-variable chain rule teaches us how to differentiate composite functions, which is a skill that directly translates to working with functions of multiple variables. By mastering this concept, students can more easily grasp the extended principles applied in multivariable calculus.

    Another critical prerequisite is understanding composite functions. These functions, where one function is nested inside another, form the basis of the chain rule. In multivariable calculus, we often encounter situations where functions are composed of multiple variables, each potentially dependent on others. A strong grasp of how composite functions work in simpler contexts prepares students for the more complex scenarios they'll face when dealing with multivariable functions.

    The concept of rate of change is also fundamental to understanding the chain rule for multivariable functions. In single-variable calculus, we learn that derivatives represent rates of change. This idea extends to multivariable calculus, where partial derivatives represent rates of change with respect to individual variables. The chain rule for multivariable functions essentially combines these rates of change in a systematic way, making it crucial to have a solid understanding of this basic principle.

    By thoroughly understanding these prerequisite topics, students can build a strong foundation for tackling the chain rule in multivariable calculus. The single-variable chain rule provides the basic framework, while knowledge of composite functions helps in visualizing how multiple variables interact. Understanding rates of change gives meaning to the partial derivatives involved in the multivariable chain rule.

    As students progress to more advanced topics, they'll find that these prerequisites continue to play a vital role. The chain rule for multivariable functions is not just an isolated concept but a powerful tool that builds upon these fundamental ideas. It's used extensively in optimization problems, thermodynamics, and various fields of engineering and physics.

    In conclusion, mastering these prerequisite topics is not just about preparing for a single concept. It's about developing a comprehensive understanding of calculus that will serve students well throughout their mathematical journey. By investing time in these foundational concepts, students set themselves up for success in grasping the chain rule for multivariable functions and beyond.