Equation of a Plane
Couple sections ago, we saw that the equation of plane can be expressed as . However, this equation does not give much information. So suppose we have the following graph:
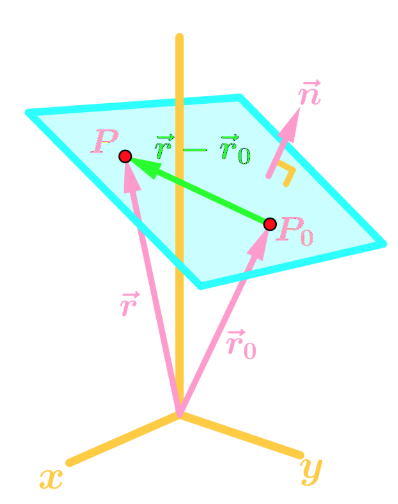
Where and are position vectors for points and respectively, and is a normal vector that is orthogonal (perpendicular) to the plane.
Since is on the plane, then is orthogonal to . In other words, their dot products should give 0.
So,
The key to finding the equation of a plane is finding two things:
- The normal vector (orthogonal to the plane)
- A point on the plane.






