Long run cost
 Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Get the most by viewing this topic in your current grade. Pick your course now.
Intros
Lessons
- Short Run Cost Overview:
- Long-Run Production Function
- Both labour and capital vary
- Table for Production Function
- Diminishing returns of marginal product of labour
- Diminishing returns of marginal product of capital
- Short-Run Costs & Total Average Costs
- All ATC curves are U-shaped
- More machines = bigger output at minimum average cost
- Planned output → find the lowest possible cost
- Long-Run Average Cost
- LRAC: Long Run Average Cost
- Lowest attainable cost across all ATC curves
- What it looks like
- Economies & Diseconomies of Scale
- Economies of Scale: average cost as output , falling LRAC
- Diseconomies of Scale: average cost as output , rising LRAC
- Constant Returns to Scale: average cost unchanged as output , horizontal LRAC
- Minimum Efficient Scale
Examples
Lessons
- Finding the Average Total Costs
Suppose the cost of each machine is $50, and the cost of each worker per week is $50. Using the following table to calculate and graph the ATC curves for factories 1 and 2.Labour (workers per week)
Output (Clothes per week)
Factory 1
(1 machine)
Factory 2
(2 machines)
Factory 3
(3 machines)
Factory 4
(4 machines)
1
10
30
45
55
2
30
50
65
75
3
45
65
80
90
4
55
75
90
100
5
60
80
95
105
- Suppose the cost of each machine is $50, and the cost of each worker per week is $50. Using the following table to calculate and graph the
ATC curves for factories 3 and 4.
Labour (workers per week)
Output (Clothes per week)
Factory 1
(1 machine)
Factory 2
(2 machines)
Factory 3
(3 machines)
Factory 4
(4 machines)
1
10
30
45
55
2
30
50
65
75
3
45
65
80
90
4
55
75
90
100
5
60
80
95
105
- Understanding the Long-Run Cost Curve
Suppose you are given 4 ATC curves on the following graph.
- Suppose you are given 4 ATC curves on the following graph.
Topic Notes
In the long run, all inputs and costs are variables.
Long-run Production Function: the relationship between the output and the quantities of both capital and labour.
The function is not graphable in a 2D graph, but it can be shown in a table.
|
Labour (workers per week) |
Output (Cars per week) |
|||
|
Factory 1 (1 machine) |
Factory 2 (2 machines) |
Factory 3 (3 machines) |
Factory 4 (4 machines) |
|
|
1 |
9 |
14 |
17 |
19 |
|
2 |
14 |
19 |
22 |
24 |
|
3 |
17 |
22 |
25 |
27 |
|
4 |
19 |
24 |
27 |
29 |
|
5 |
20 |
25 |
28 |
30 |
Marginal Product of Capital: the additional total product from a one-unit increase of capital.
Diminishing Returns of Labour: can be shown by allowing labour to vary and keeping capital constant.
Diminishing Returns of Capital: can be shown by allowing capital to vary and keeping labour constant.
Each column of the table could be graphed as a total product curve for each factory.
Short-Run Costs & Total Average Cost
Recall that the total average cost is:
We can use this formula to calculate the short-run average total cost for each factory. Suppose the cost for each worker is $10, and the cost for each machine is 10$.
Then for factory 1 and 2, you get the following table,
|
# of Machines & Labour |
TC |
Q |
ATC1
|
|
1 machine, 1 worker |
20 |
9 |
$2.22 |
|
1 machine, 2 workers |
30 |
14 |
$2.14 |
|
1 machine, 3 workers |
40 |
17 |
$2.35 |
|
1 machine, 4 workers |
50 |
19 |
$2.63 |
|
1 machine, 5 workers |
60 |
20 |
$3.00 |
|
# of Machines & Labour |
TC |
Q |
ATC2
|
|
2 machine, 1 worker |
30 |
14 |
$2.14 |
|
2 machine, 2 workers |
40 |
19 |
$2.11 |
|
2 machine, 3 workers |
50 |
22 |
$2.27 |
|
2 machine, 4 workers |
60 |
24 |
$2.50 |
|
2 machine, 5 workers |
70 |
25 |
$2.80 |
Then for factory 3 and 4, we will get
|
# of Machines & Labour |
TC |
Q |
ATC3
|
|
3 machine, 1 worker |
40 |
17 |
$2.35 |
|
3 machine, 2 workers |
50 |
22 |
$2.27 |
|
3 machine, 3 workers |
60 |
25 |
$2.40 |
|
3 machine, 4 workers |
70 |
27 |
$2.59 |
|
3 machine, 5 workers |
80 |
28 |
$2.86 |
|
# of Machines & Labour |
TC |
Q |
ATC4
|
|
4 machine, 1 worker |
50 |
19 |
$2.63 |
|
4 machine, 2 workers |
60 |
24 |
$2.50 |
|
4 machine, 3 workers |
70 |
27 |
$2.59 |
|
4 machine, 4 workers |
80 |
29 |
$2.76 |
|
4 machine, 5 workers |
90 |
30 |
$3.00 |
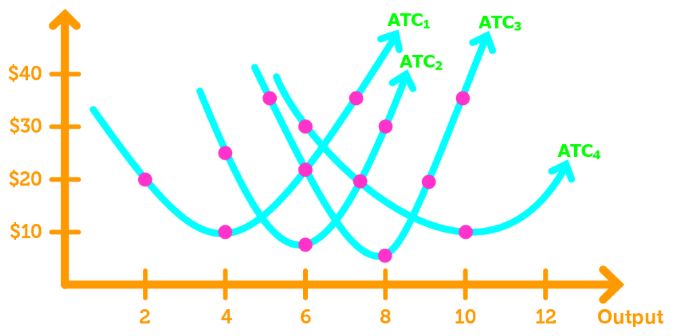
We can now graph all the ATC curves into one graph.
Note 1: All ATC curves are U shaped.
Note 2: The more machines there are, the bigger the output is at which average total cost is at a minimum.
Long Run Average Cost
Long-Run Average Cost (LRAC) is the relationship between the lowest average total cost attainable and output when the firm can change both the factories and the number of labours it employs.
To draw the LRAC, we draw a curve that is tangent to all ATC's.
Economies & Diseconomies of Scale
Economies of Scale: the area in which the LRAC decreases as output increases.
Diseconomies of Scale: the area in which LRAC increases as output increases.
Constant Returns to Scale: the area in which LRAC is horizontal as output increases.
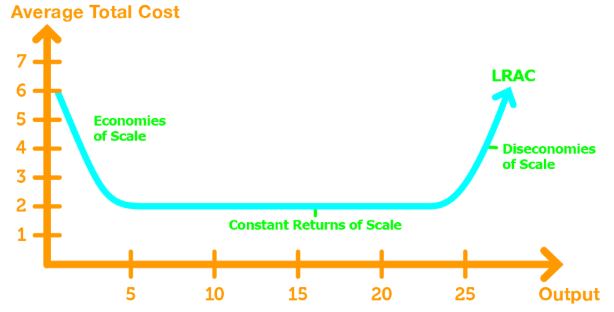
Minimum Efficient Scale: the point in the LRAC curve where the lowest possible cost is attained.