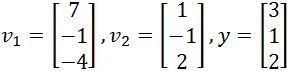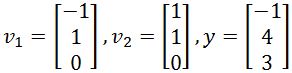Orthogonal projections
What is an orthogonal projection
The orthogonal projection of a vector onto another is, just as the name says it, the projection of the first vector above the second one. You may be wondering what is that supposed to mean then?, well, for a better explanation let us show you graphically in the next figure: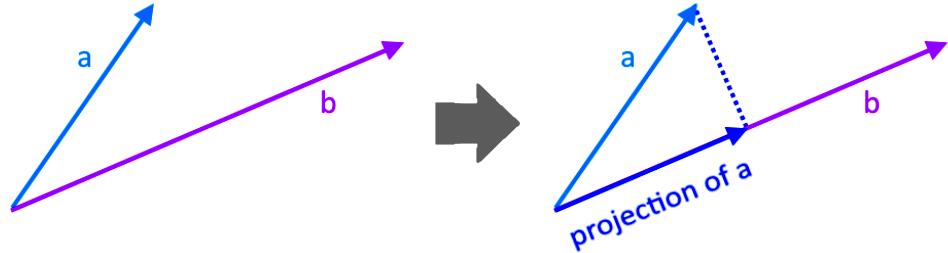
Notice that in the right hand side of the figure we can see how we added the vector which is the orthogonal projection of a onto b. The word orthogonal (which you know already that it means there is perpendicularity involved) comes from the angle made by the projection and the normal line connecting the projection and the original vector, for this case, this normal line (the dashed line in figure 1) is the component of vector a that is orthogonal to b, and can its length can be written as: .
Orthogonal projection vector
A formal orthogonal projection definition would be that it refers to the projection of a vector onto a plane which is parallel to another vector, in other words and taking figure 1 in mind, the projection of vector a falls in the same plane as vector , and so, the projection of vector is a vector parallel to vector .
And so, if we consider a subspace spanned by the vector , then the orthogonal projection of onto is defined as and can be calculated with the next equation:
Where is called the orthogonal projection vector, and so, equation 1 may be referred to (in general) as the orthogonal projection formula .
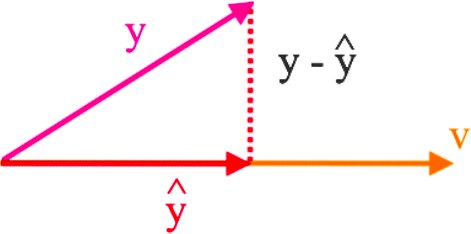
Notice the component of y orthogonal to v is equal to .
Now let us talk about orthogonal projections onto a subspace, not another vector, but a plane. For that:
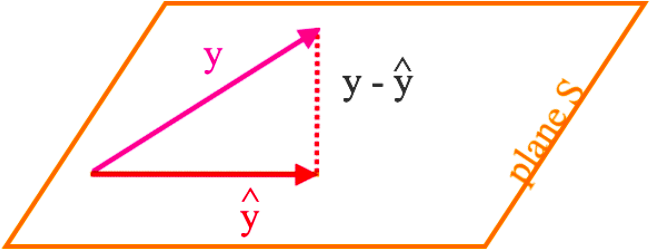
Let be a subspace in , then each vector in can be written as:
Where is in and is in . And so, is the orthogonal projection of onto .
Therefore, if we want to calculate we need to check if {} is an orthogonal basis of , if the vectors from the subset happen to form an orthogonal set and orthogonal basis (which remember, this can be checked by performing the dot product of all of the vectors in the set) then we can calculate the projection of onto as:
However, if {} is an orthonormal basis of , then the equation changes a little bit:
Remember that an orthonormal basis is a basis conformed by a set of vectors which are orthogonal with each other AND at the same time they are all unit vectors themselves.
How to find orthogonal projection
The steps to find the orthogonal projection of vector y onto a subspace are as follows:
- Verify that the set of vectors provided is either an orthogonal basis or an orthonormal basis
- If orthogonal basis continue on step 2
- If orthonormal basis continue on step 3
- Having an orthogonal basis containing a set of vectors {}, compute the projection of onto by solving the formula found in equation 2. In order to do that, follow the next steps:
- Calculate the dot products
- Calculate the dot products
- Compute the divisions
- Multiply each result from our last step with its corresponding vector {}
- Add all of the resulting vectors together to find the final projection vector.
- Having an orthonormal basis containing a set of vectors {}, compute the projection of onto by solving the formula found in equation 3. In order to do that, follow the next steps:
- Calculate the dot products
- Multiply each result from our last step with its corresponding vector {}
- Add all of the resulting vectors together to find the final projection vector.
And now you are ready to solve some exercise problems!
Orthogonal projection examples
Example 1
Assume that {} is an orthogonal basis for . Write as a sum of two vectors, one in Span{} and one in Span{}. The vectors and are defined as follows: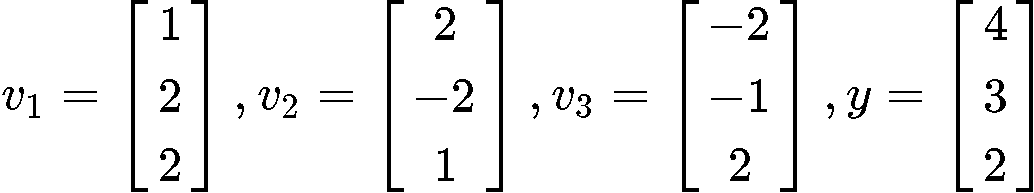
For this first problem we are already assuming that the vectors provided form an orthogonal basis in , that means each vector is orthogonal to each other, and linearly independent. Therefore the spans Span{} and Span{} each have basis {} and {} containing orthogonal vectors which makes them linearly independent, these characteristics make them orthogonal bases!.
Therefore, we can be sure already that we can use equation 2 in order to solve for when needed, in BOTH cases: as a sum of two vectors in Span{} and as a sum of two vectors in Span{}.
If we need to write y as a sum of two vectors, remember from figures 2 and 3 that ,
And so, we calculate first and then add it to .
We will work only on the first part of the problem writing as a sum of two vectors in Span{} and leave the second case for you to solve on your own.
So let us calculate !
For this case we have only one vector in the basis of the span , and so, the formula goes as:
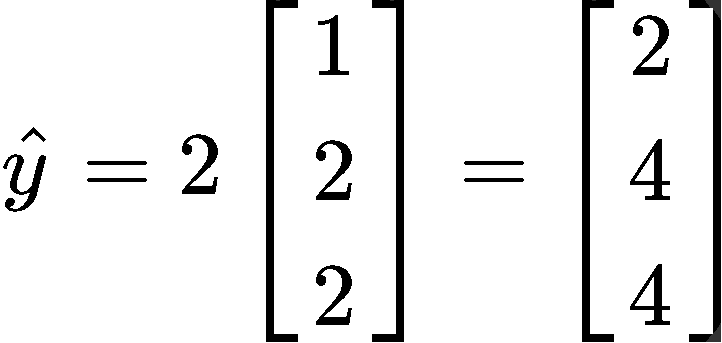
With that we can now write y as a sum of two vectors in Span{} as follows:
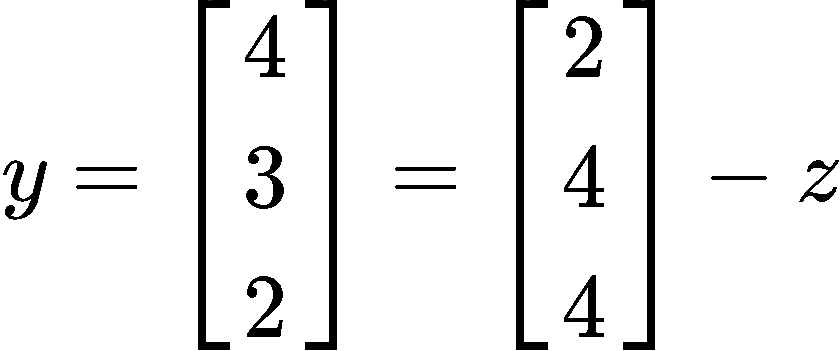
And what is ? Easy! We can calculate it just to see what it is:
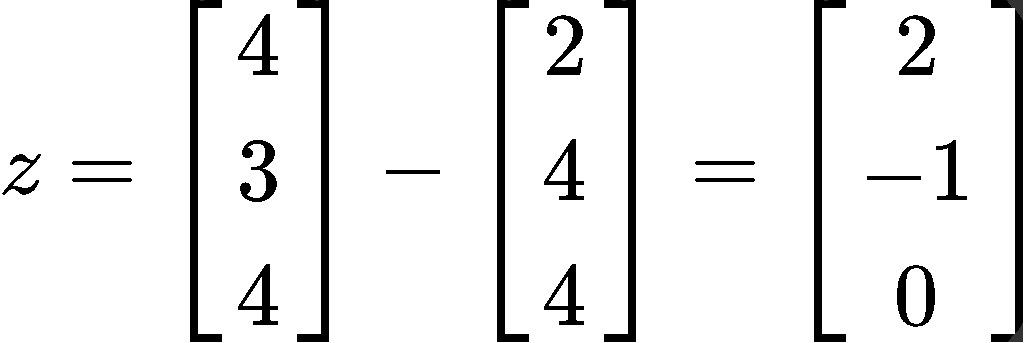
Example 2
Verify that {} is an orthonormal set, and then define orthogonal projection of onto Span {}.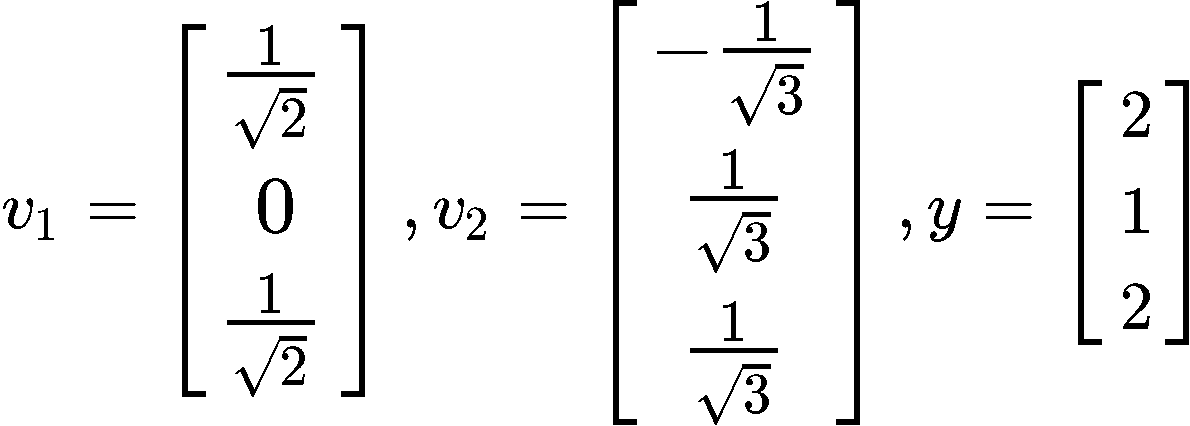
To verify if the set {} is orthonormal we first check if the vectors in the set are orthogonal to each other by computing their dot product:
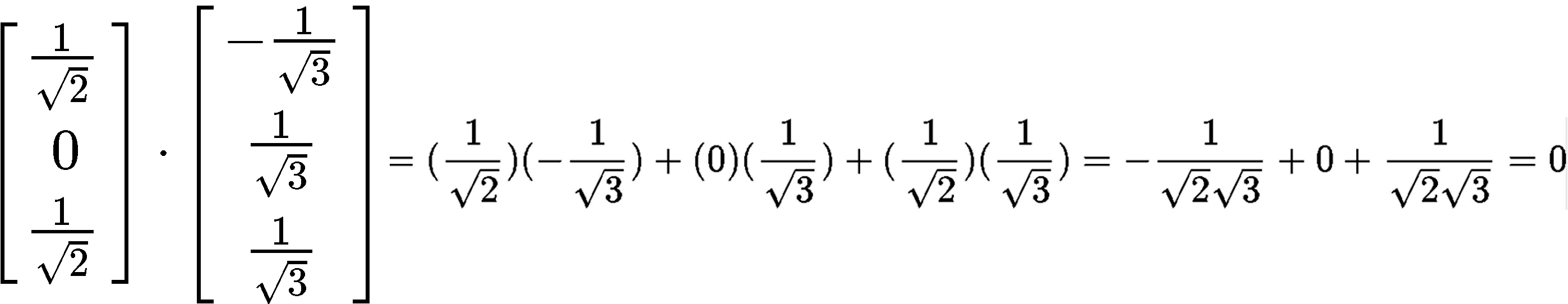
Since the dot product yielded a result of zero, then it means the vectors are orthogonal to each other. The second condition for the set to be an orthonormal set is that its vectors are unit vectors, thus, let us check if their magnitude is one.
And so, we have an orthonormal set since we just proved that the vectors and are unit vectors. Now we have to find the orthogonal projection of y onto Span {}.
Using this equation, we plug the values that we have for vectors and in order to calculate the projection vector :
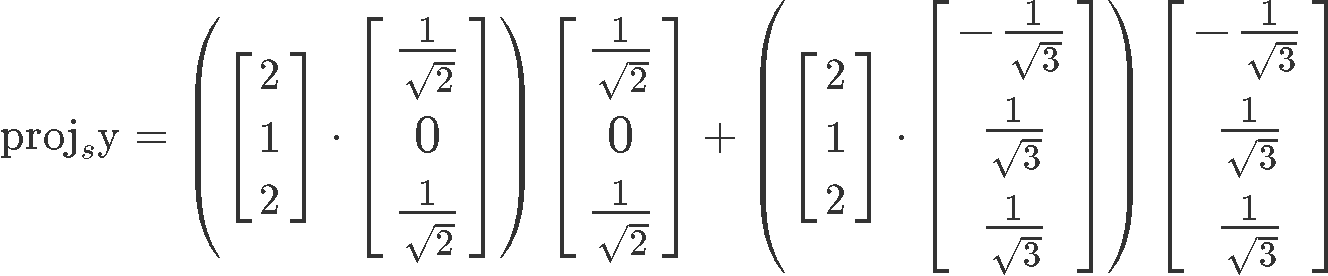
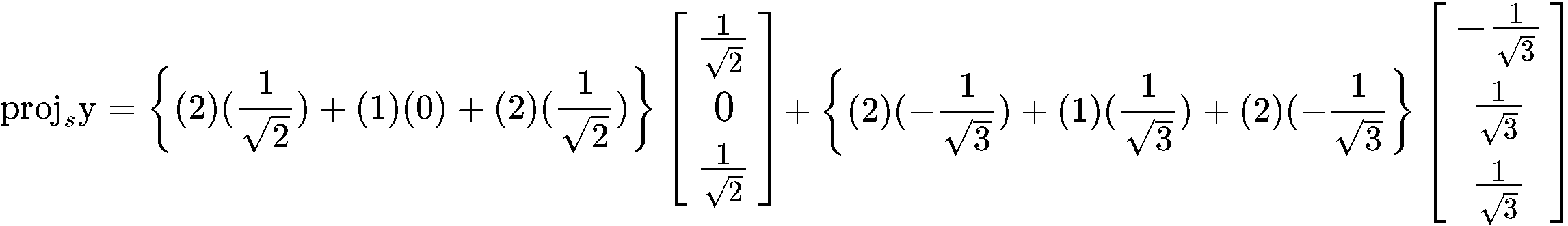
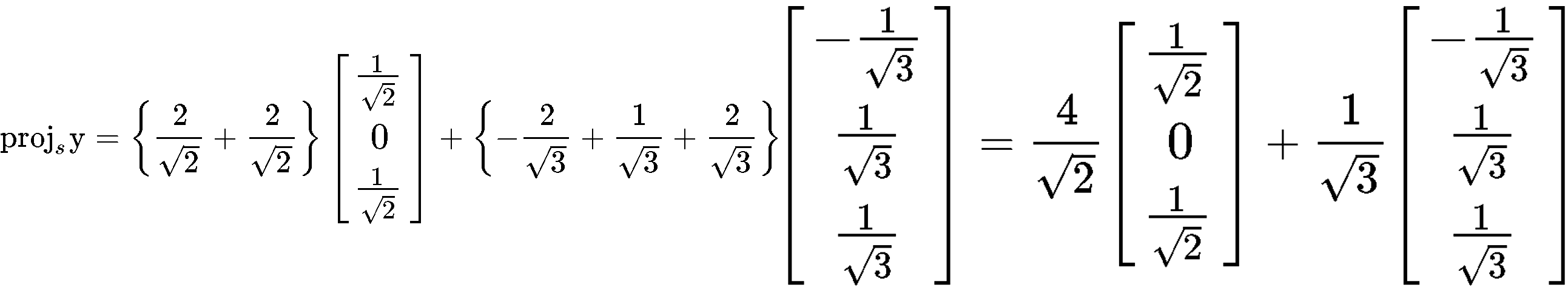
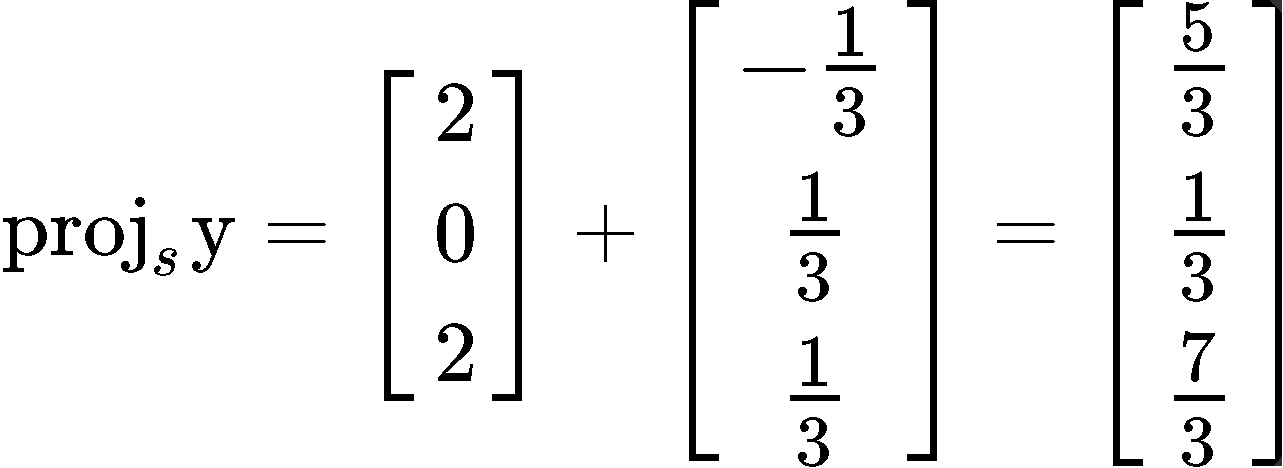
Example 3
Find the best approximation of by vectors of the form , where: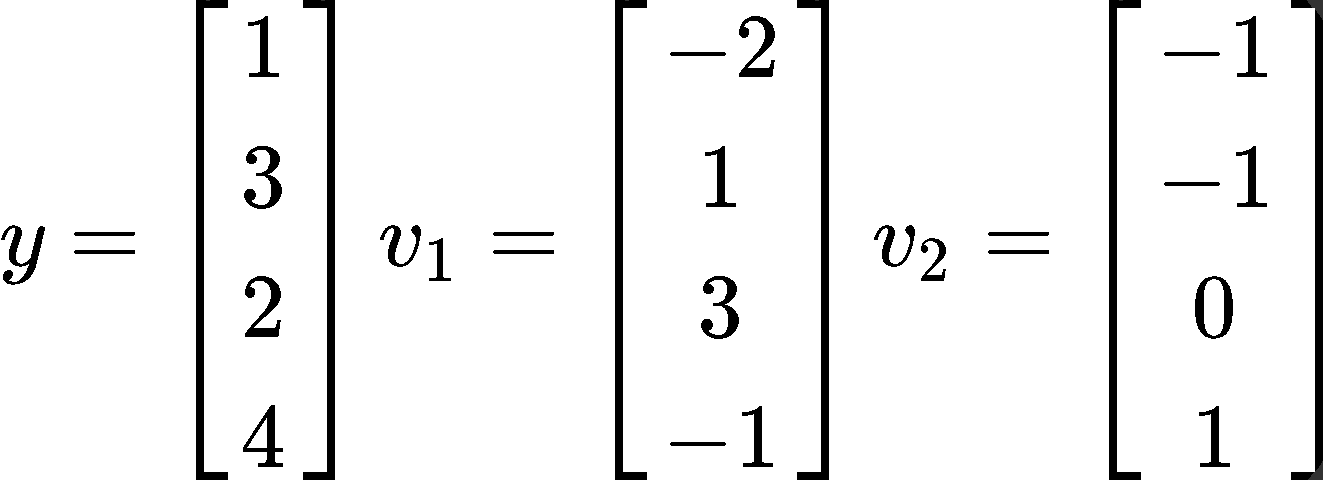
Having vectors of the form means that we have a linear combination that is the same as having a span of vectors, in this case, the span of vectors and . And so, we can obtain a basis such as:
Now the first thing to do in order to find the best approximation of y is to check if the basis provided is an orthogonal basis, for that, we obtain the inner product of the two vectors inside the basis:
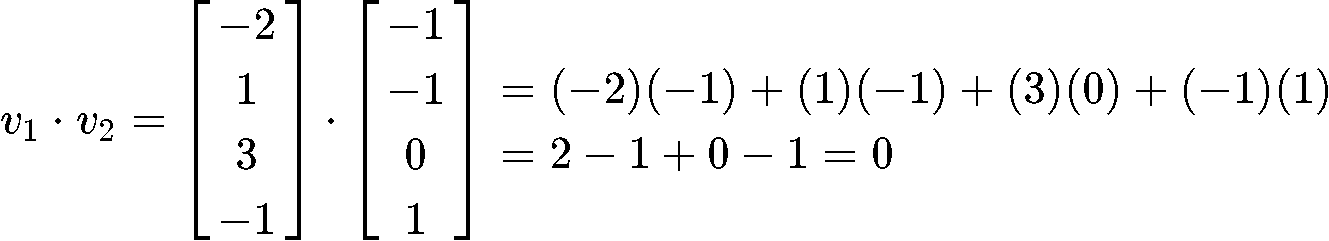
And given that the set is an orthogonal set due the inner product above resulting in a zero, we can now finally compute the vector (which is the best approximation of ) by using the projection formula shown in equation 2 as shown below:
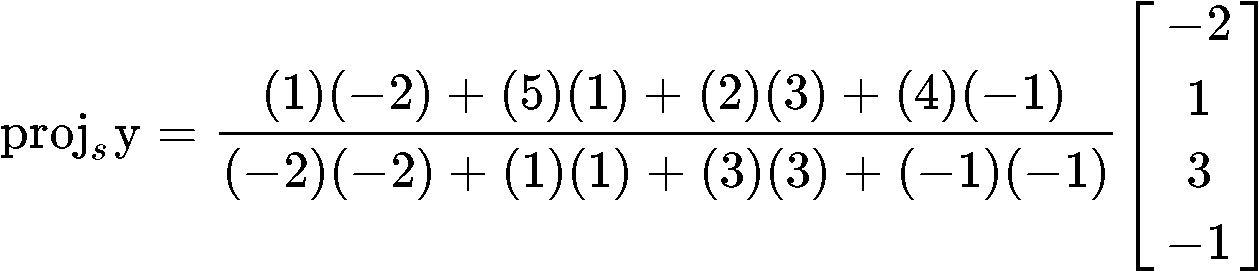
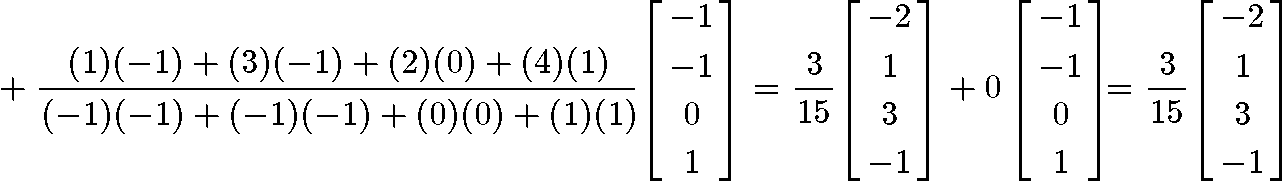
Example 4
Find the closest point to in the subspace spanned by and :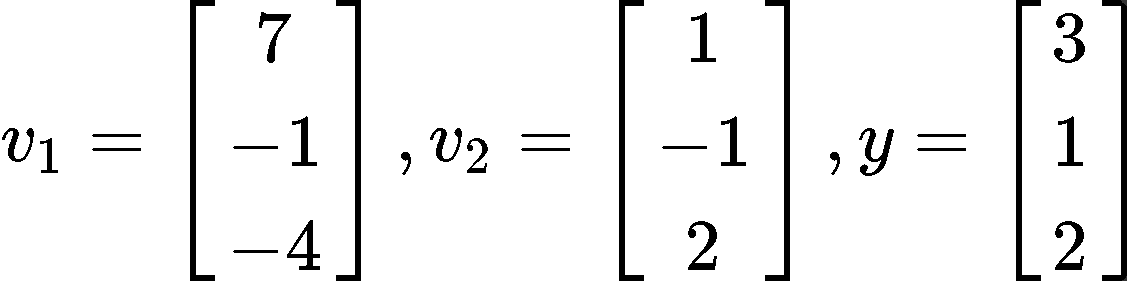
The closest point to is simply since its the shortest distance compared to any other vector given that is the best approximation of itself. And so, the purpose of this problem is to calculate .
For that we will use equation 2 once more in order to calculate the orthogonal projection of y onto , but the problem is that at this point we need more information for us to use that equation.
First we need to check if we have an orthogonal basis for .
In here we have a subspace spanned by and , which means that we have the linear combination of and (so and are linearly independent) which is equal to the basis Span{}. In order to check if this basis is an orthogonal basis, we have to see if and are orthogonal to each other, therefore, we compute their dot product!
And so, we have an orthogonal basis since the dot product above yielded a result of zero.
So now we can calculate using equation 2:
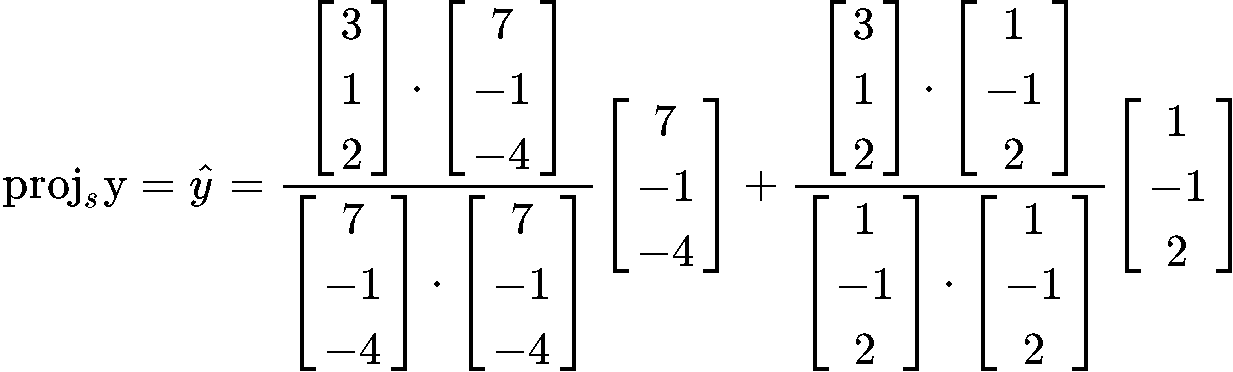
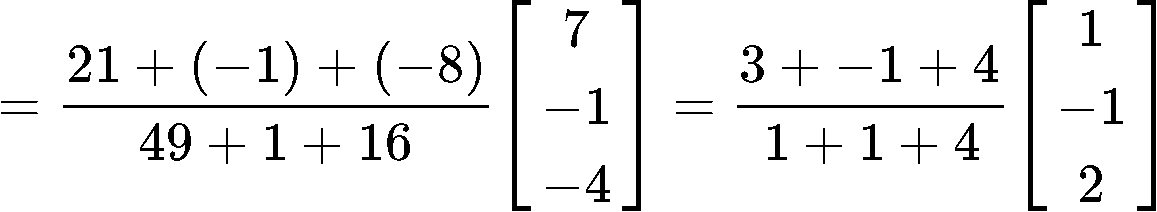
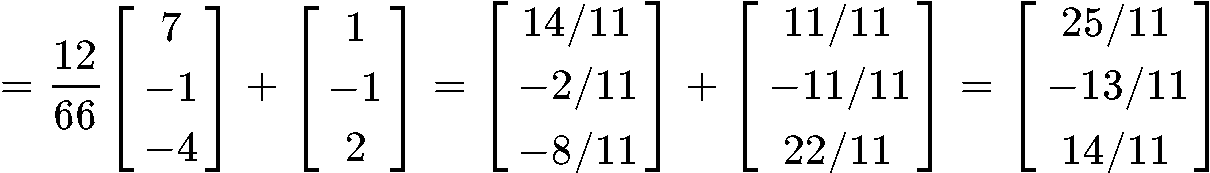
Example 5
Find the closest distance from to Span{} if and are defined as below: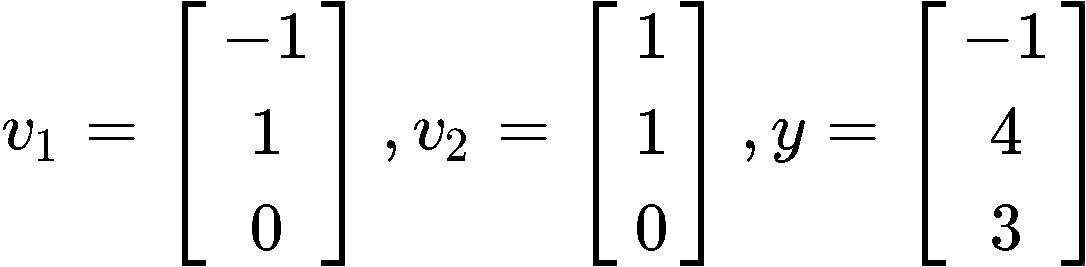
In this case, the closest distance from to can be graphically represented below:
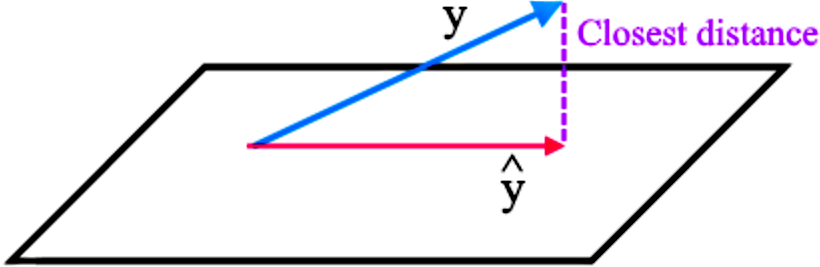
Therefore the closest distance is equal to the magnitude of the subtraction of the vector and , therefore the closest distance
So if we want to calculate the closest distance, we need to compute and for that, we first need to check that we have an orthogonal basis, and so, we check for an orthogonal basis by calculating the dot product of and :
Knowing that we have an orthogonal basis due the result above, we can now compute :
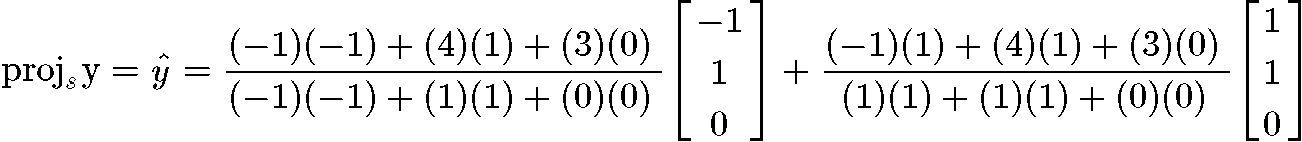
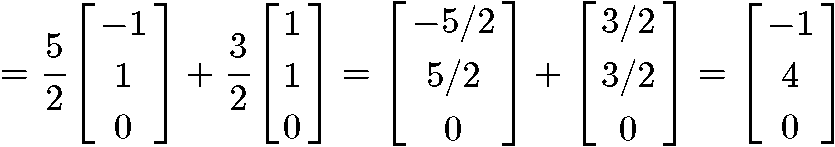
And now that we have the vector we can finally compute the length :
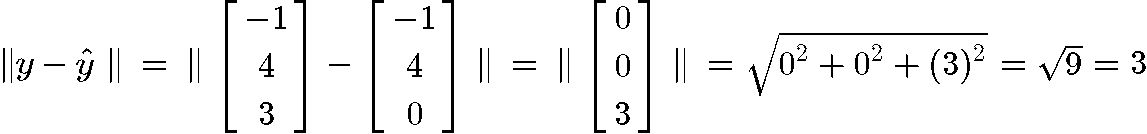
And so, we have arrived to the end of our lesson, we hope you enjoyed it and see you in the next topic!
The Orthogonal Decomposition Theorem
Let be a subspace in . Then each vector in can be written as:
where is in and is in . Note that is the orthogonal projection of onto
If {} is an orthogonal basis of , then
However if {} is an orthonormal basis of , then
Property of Orthogonal Projection
If {} is an orthogonal basis for and if happens to be in , then
In other words, if y is in Span{}, then .
The Best Approximation Theorem
Let be a subspace of . Also, let be a vector in , and be the orthogonal projection of onto . Then is the closest point in , because
<
where are all vectors in that are distinct from .
Let be a subspace in . Then each vector in can be written as:
where is in and is in . Note that is the orthogonal projection of onto
If {} is an orthogonal basis of , then
However if {} is an orthonormal basis of , then
Property of Orthogonal Projection
If {} is an orthogonal basis for and if happens to be in , then
In other words, if y is in Span{}, then .
The Best Approximation Theorem
Let be a subspace of . Also, let be a vector in , and be the orthogonal projection of onto . Then is the closest point in , because
where are all vectors in that are distinct from .

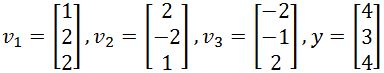
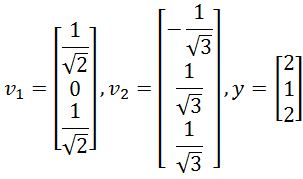
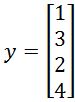 , and
, and 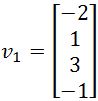 ,
, 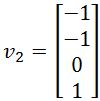 .
.