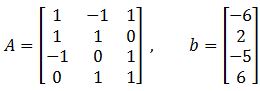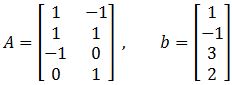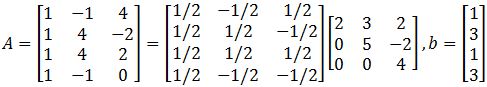Least-squares problem
Method of least squares
In linear algebra, we have talked about the matrix equation Ax=b and the unique solutions that can be obtained for the vector , but, sometimes does not have a solution, and so, for those cases our best approach is to approximate as much as possible a value for .
Therefore, the topic for the lesson of today is a technique dedicated to obtain that close-enough solution. The technique has been called least-squares and is based on the principle that since we cannot obtain the solution of the vector for the matrix equation , then we have to find an that produces a multiplication as close as possible to the vector
If is an matrix and is a vector in , then the least-squares solution for is the vector in where the following condition applies for all in :
This means that if we cannot obtain a solution for the equation , then our best approximation to the true value of , which we call or the least-squares solution (also called the least squares approximation), can be obtained if the condition in equation 1 is met. The left hand side on this equation is what we call the magnitude of the smallest possible error of the best approximation to the vector , in other words, is the smallest possible error in . The right hand side is the smallest possible error in .
Having seen how the method of least squares is related to errors, we can talk about how this relates to a real life scenario. Basically, the idea of the least square method is that as much as we want to be accurate while performing measurements during studies or experiments, the truth is that there is just so much precision we can obtain as humans with non-perfect tools in a non-perfect world. From the scale of the measurements, to random changes in the environment, etc. There will be scenarios in which our measurements are not good enough and for that we have to come up with a solution that approximates as much as possible to the true value of the element we are measuring. This is where the least-squares solution brings a way to find a value that otherwise is unattainable (and actually, this is just the best approximation we can have but not the real value itself).
Least squares solution
Having a matrix and column vector in , using the next matrix equation for the relationship of the unit vector and the matrix and its transpose:
We can solve for the unit vector and we have that:
This is what is called the least-squares solution of a matrix equation
The steps to obtain the least-squares solution for a problem where you are provided with the matrix and the vector are as follows:
- If you follow the matrix equation found in equation 2:
- Find the transpose of vector
- Multiply times matrix , to obtain a new matrix:
- Multiply the transpose of matrix with the vector
- Construct the matrix equation using the results from steps b and c
- Transform the matrix equation above into an augmented matrix
- Row reduce the augmented matrix into its echelon form to find the components of vector
- Construct the least squares solution with the components found.
- If you follow the formula for that is found in equation 3:
- Start by obtaining the transpose of matrix
- Multiply times matrix , to obtain a new matrix:
- Find the inverse of matrix
- Multiply the transpose of matrix with the vector
- Multiply the results you obtained in steps 4 and 5 together to obtain:
There are also some alternative calculations in order to find the least-square solution of a matrix equation. For example: let A be a mxn matrix where are the columns of . If {} form an orthogonal set (meaning that all the columns inside matrix are orthogonal to each other), then we can find the least-squares solutions using the equation:
Where we have that encompases the orthogonal projection of b onto the columns of :
Before we continue onto the next section, let us focus for a moment in what is called the least-squares error: Remember in the first section we called the left hand side of equation 1 as the magnitude of the smallest possible error of the best approximation to the vector , in other words, the magnitude of the smallest possible error in . This part of equation one is what is called the least-squares error:
Solving least squares problems
During the next exercises we will take a look at different examples on the method of least squares. Make sure you follow all of the operations and if in doubt, do not hesitate to message us!
Example 1
Given and as shown below, find a least squares estimate solution for equation .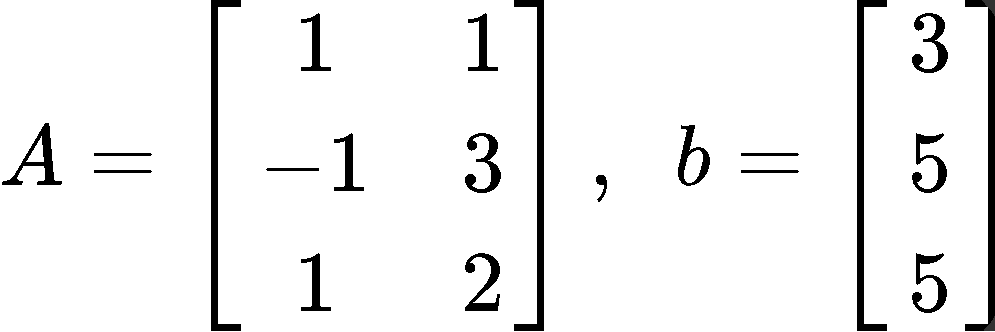
This problem is asking to solve for using the least squares formula as defined in equation 3, and so, we must follow the steps we have described before. The first thing to do is to obtain the transpose of matrix . Remember that the transpose of a matrix is obtained by swapping the elements that used to form the rows in the original matrix as the columns in the transform, and so, we swap rows to columns and columns to rows to find :
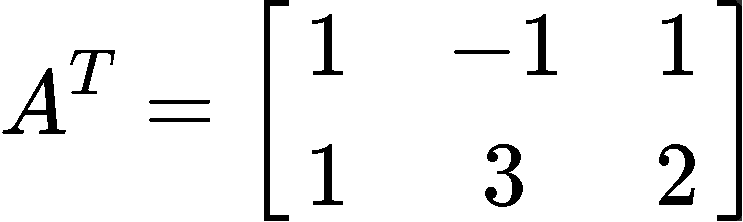
Then we multiply the matrix obtaining through the transpose in equation 8 with matrix , and so, goes as follows:
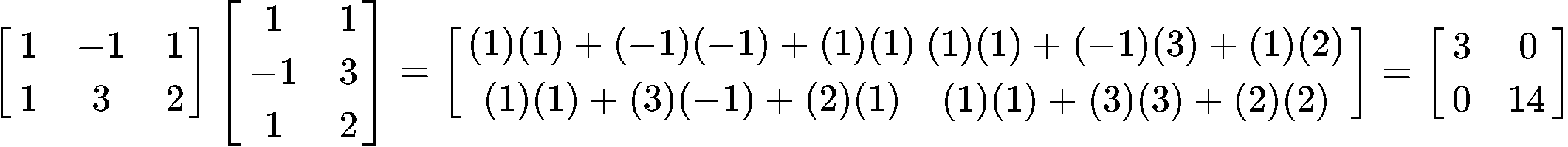
Now we find the inverse of matrix :
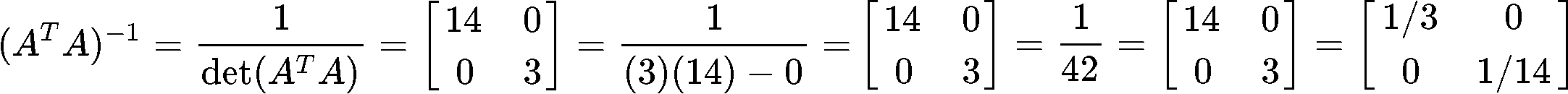
On the other hand, now we multiply the transpose of matrix , found in equation 8, with the vector :
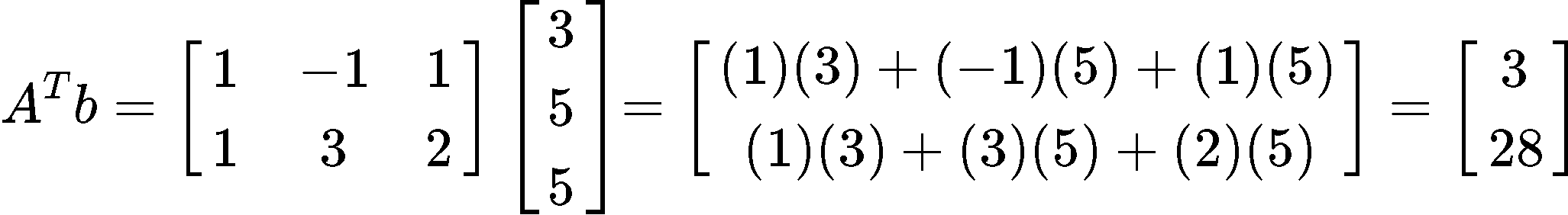
Now we can finally obtain by multiplying the results found in equations 10 and 11:
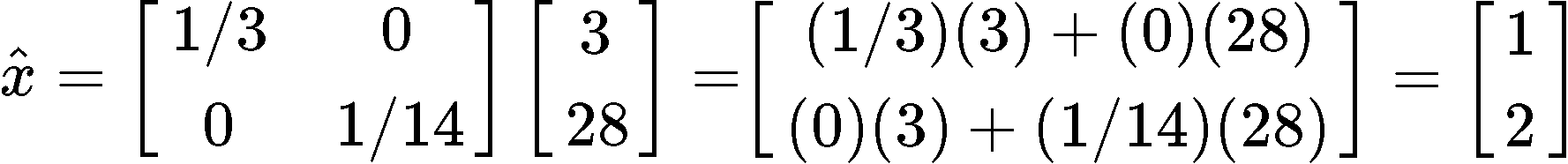
Example 2
Describe all least square solutions of equation if: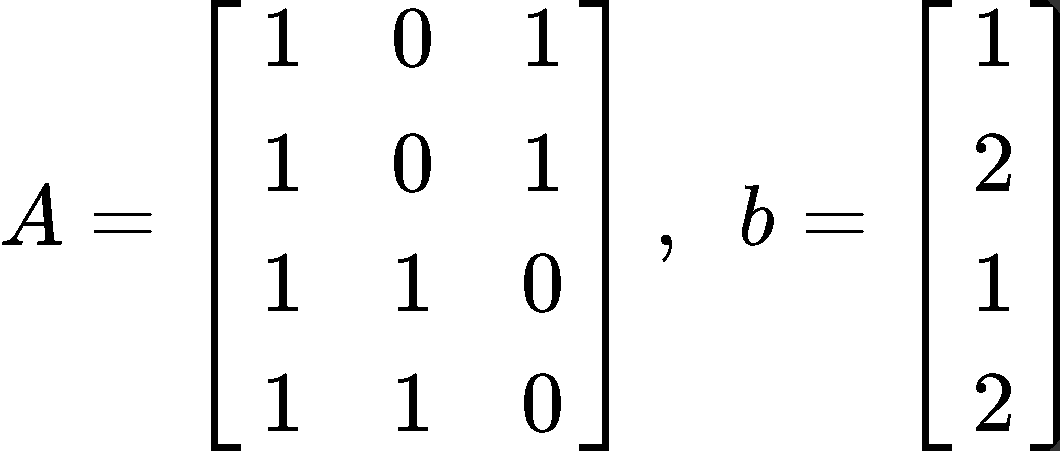
Now following the steps to solve for using the least squares equation 2:
We start by finding the transpose :
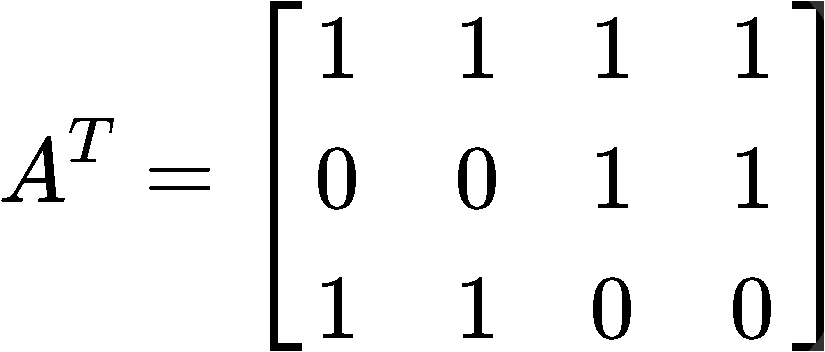
Next, we multiply the transpose to matrix :
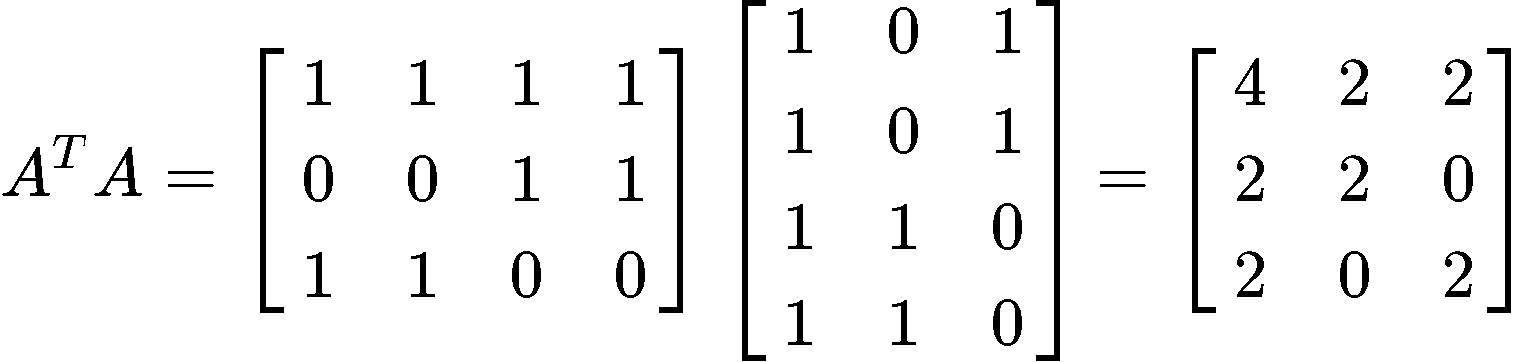
Now we multiply the transpose of matrix with the vector :
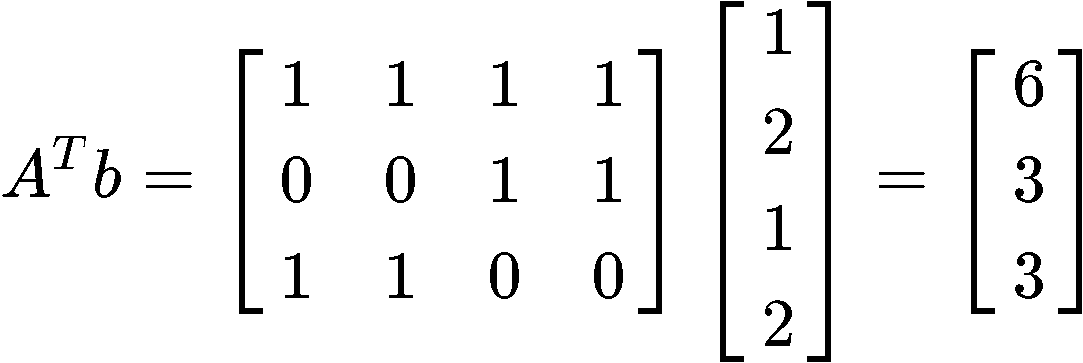
With the results found in equations 15 and 16, we can construct the matrix equation as follows:
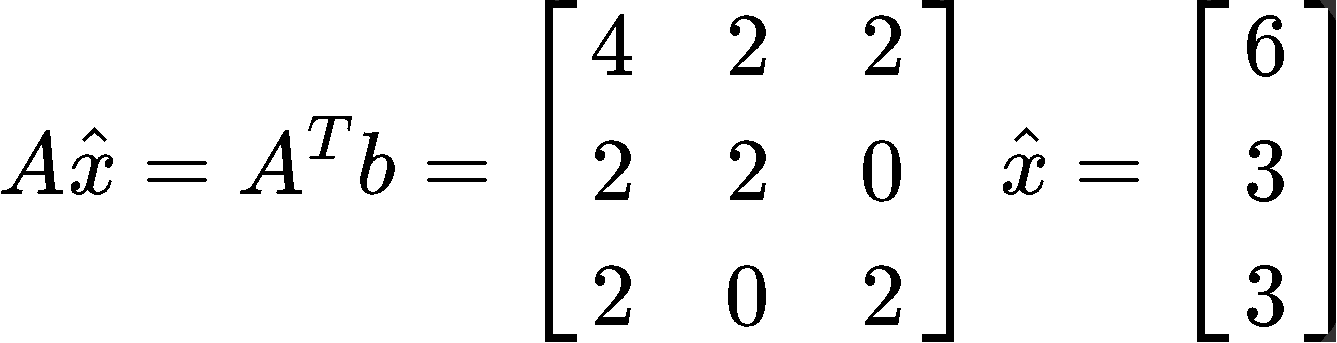
Transform the matrix equation above into an augmented matrix and row reduce it into its echelon form to find the components of vector :
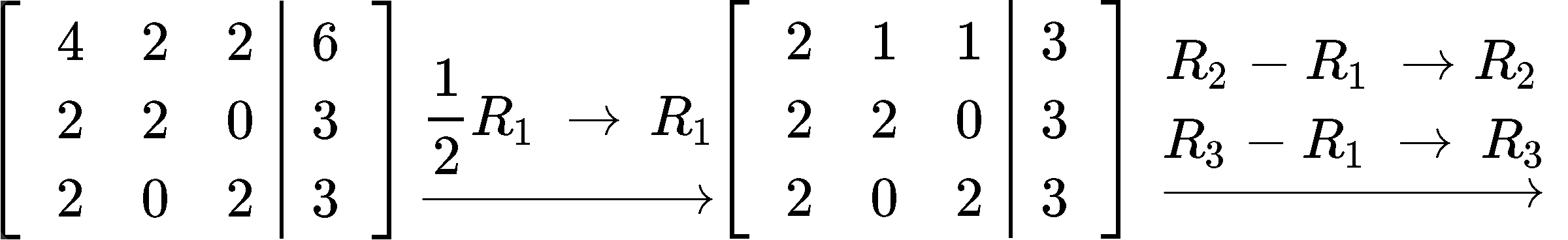
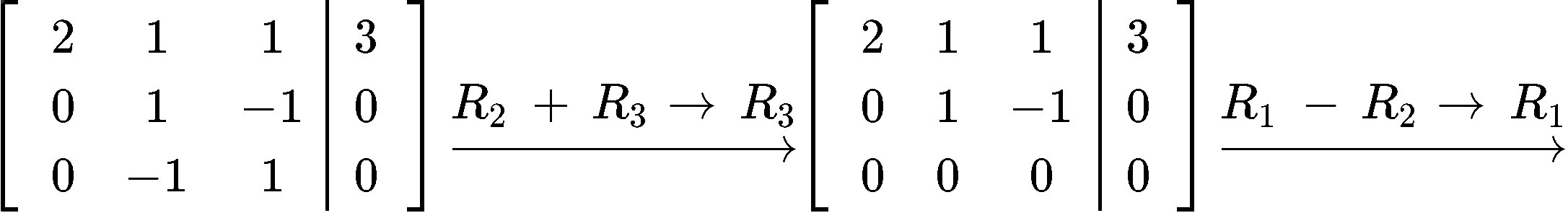
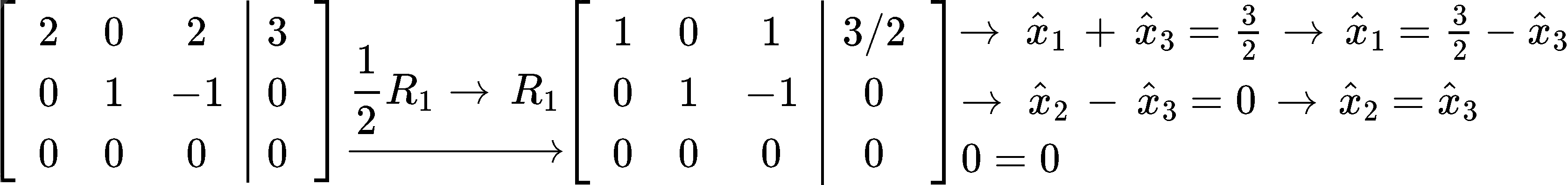
And so, we can construct the least squares solution with the components found:
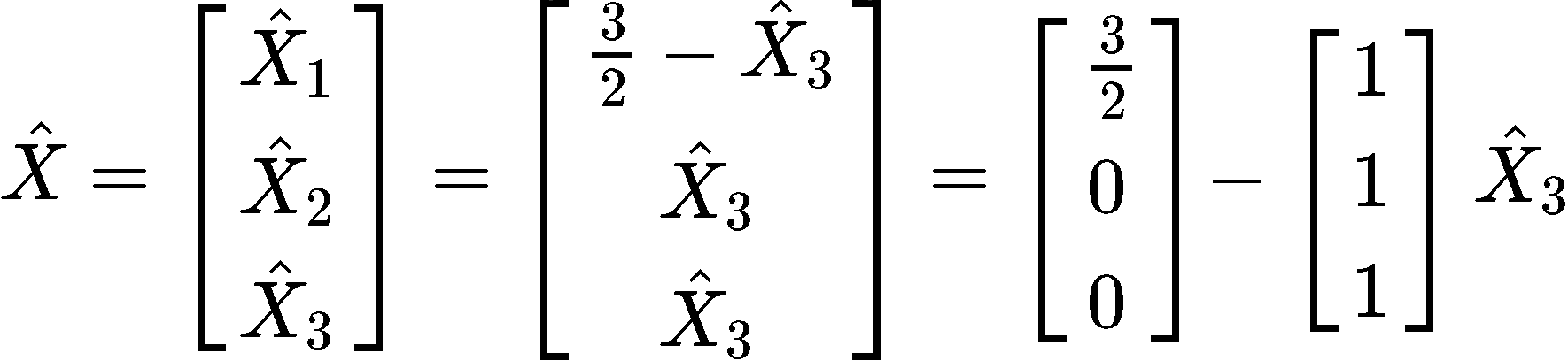
Example 3
You are given that the least squares solution of is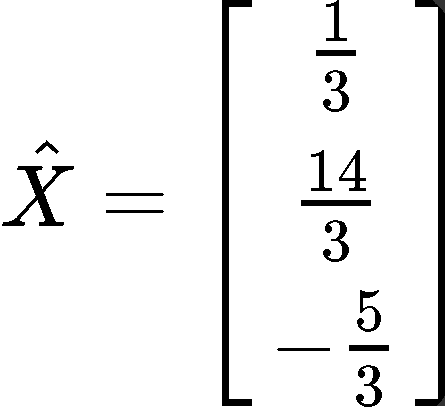
Compute the least square error if and b are as follows:
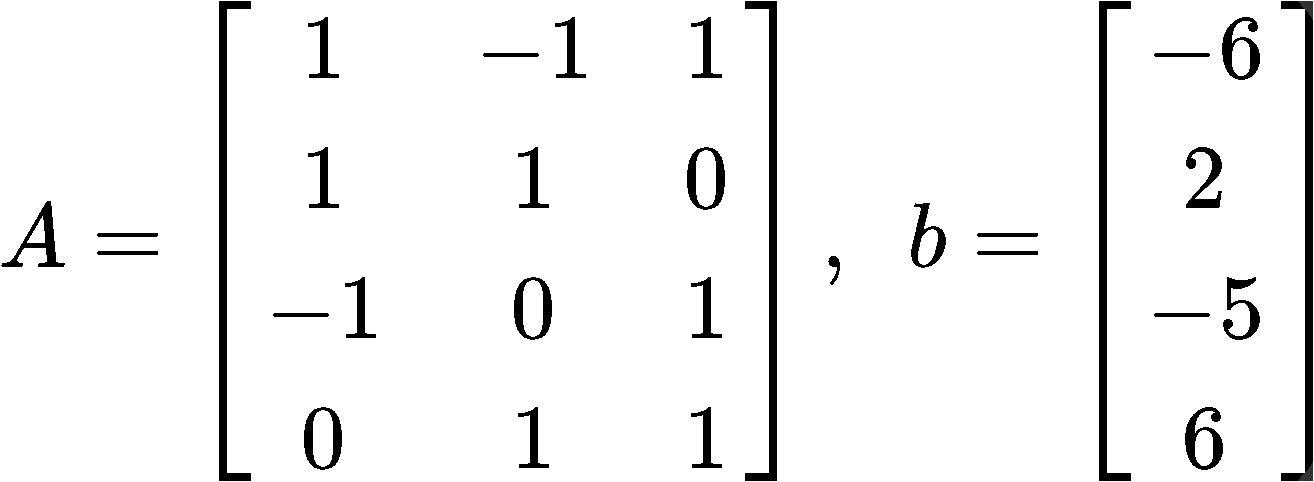
This problem is asking us to calculate the magnitude of the smallest possible error in . Such error is defined in equation 6, so now, we just have to follows the next simple steps to compute it:
Start by computing the multiplication :
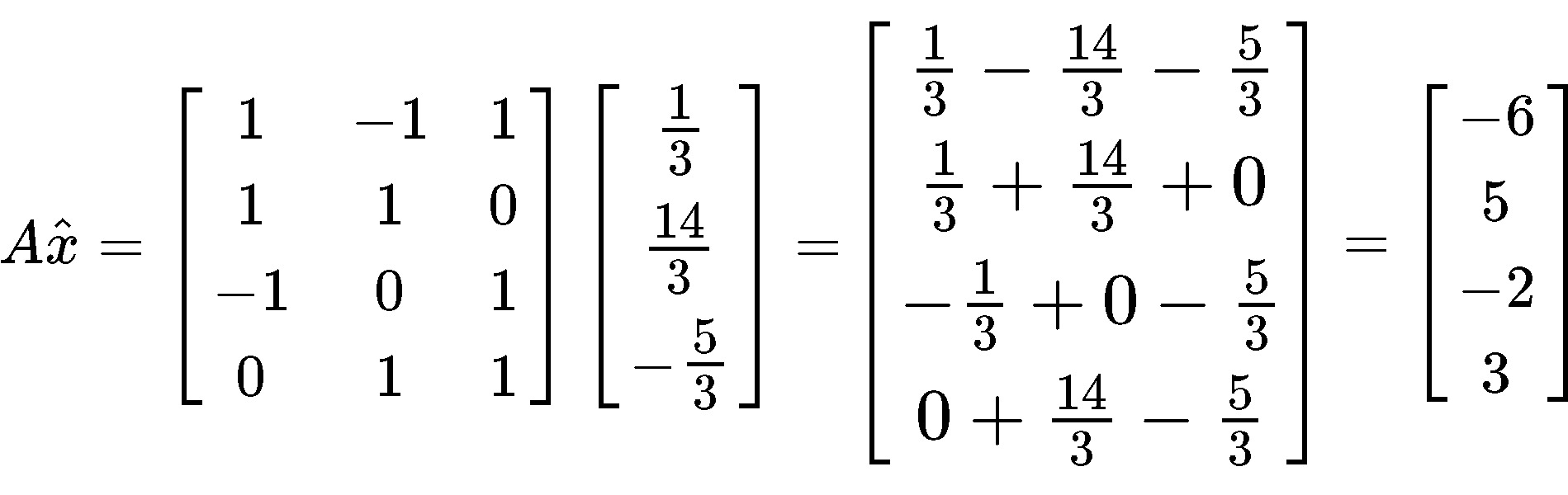
Having found the column vector from the multiplication above, we need to perform a subtraction of vectors by subtracting the vector found in equation 22 to vector b just as shown below:
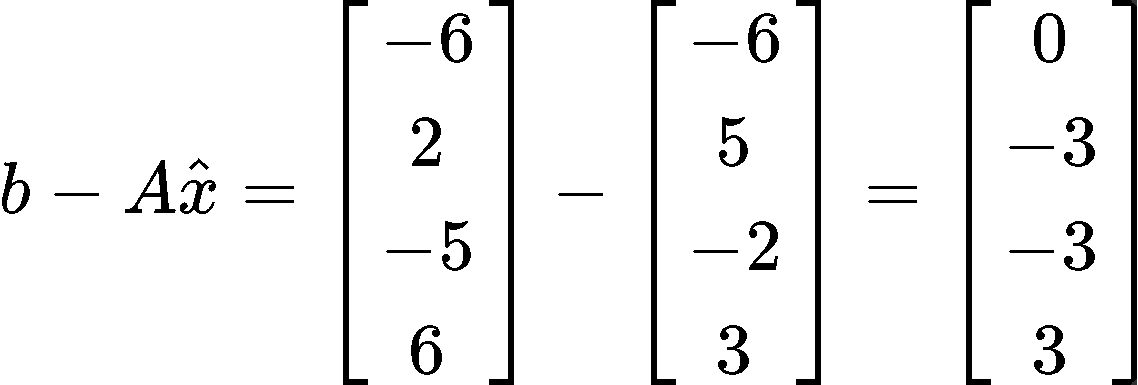
And now, you just need to find the length of the vector found in equation 23. Remember we do that by computing the square root of the addition of the components of the vectors squared:
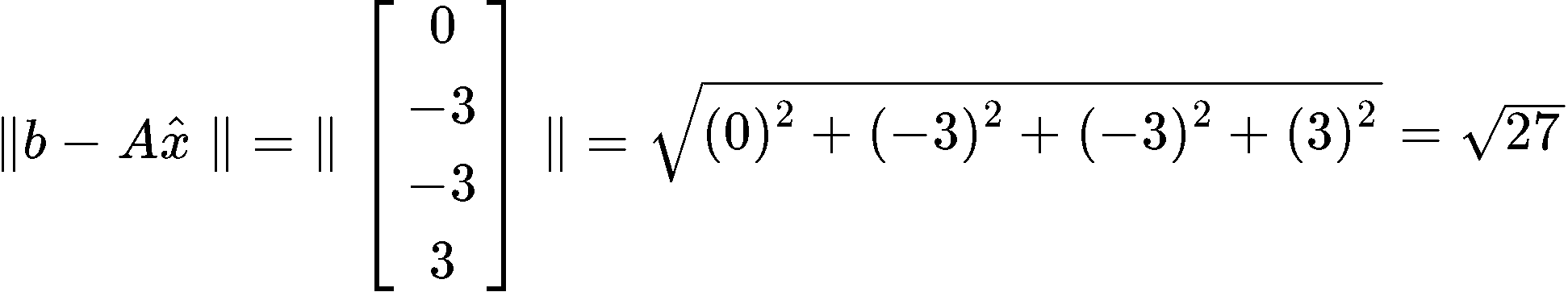
And we are done, the least square error is equal to
Example 4
Find the orthogonal projections of onto the columns of and find a least-squares solution of .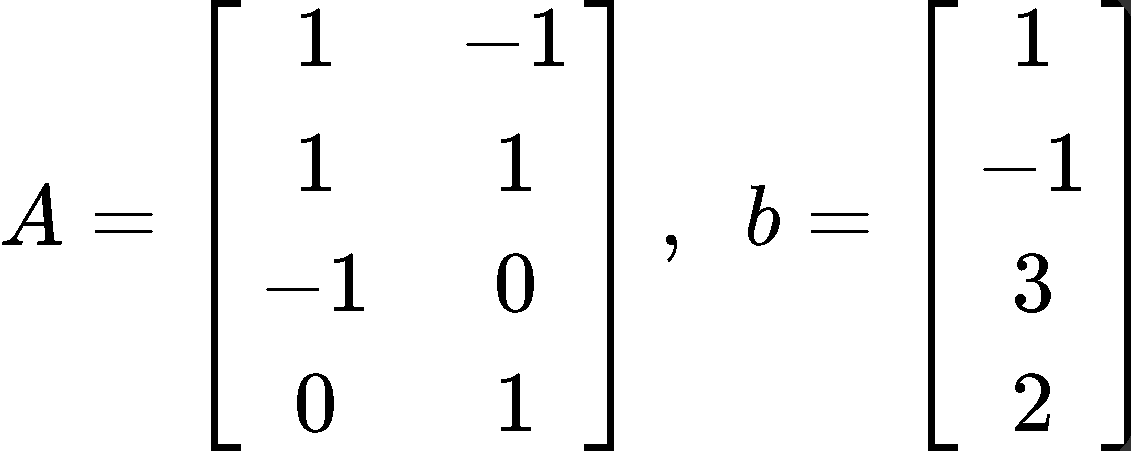
In order to find the orthogonal projections and the least squares solution for this problem we need to use and alternative approach, and so, for this case we start by computing the orthogonal projections of b onto the columns of using the formula found in equation 5, to the go ahead and solve for the least squares solution using equation 4.
For the orthogonal projections we have that:
Where and are the column vectors that compose the matrix . Therefore, solving for goes as follows:
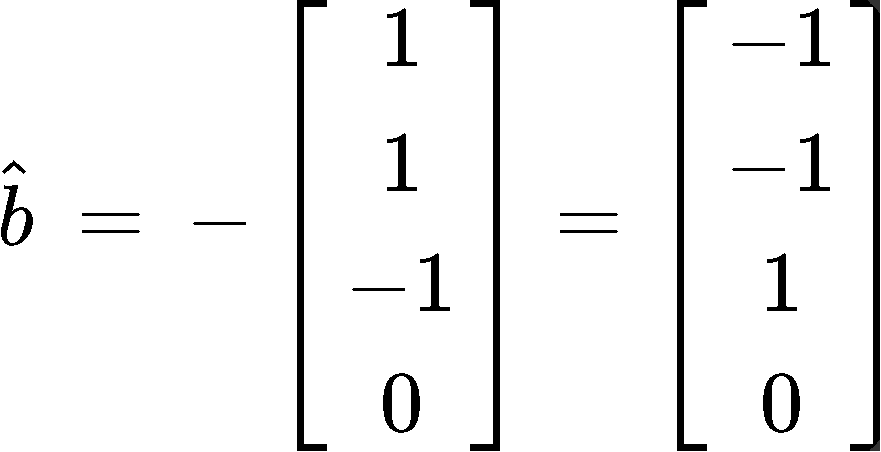
And so, we have found the orthogonal projections. Now for the least squares solution we use as reference equation 4 and take the matrix and vector so we can form the matrix equation:
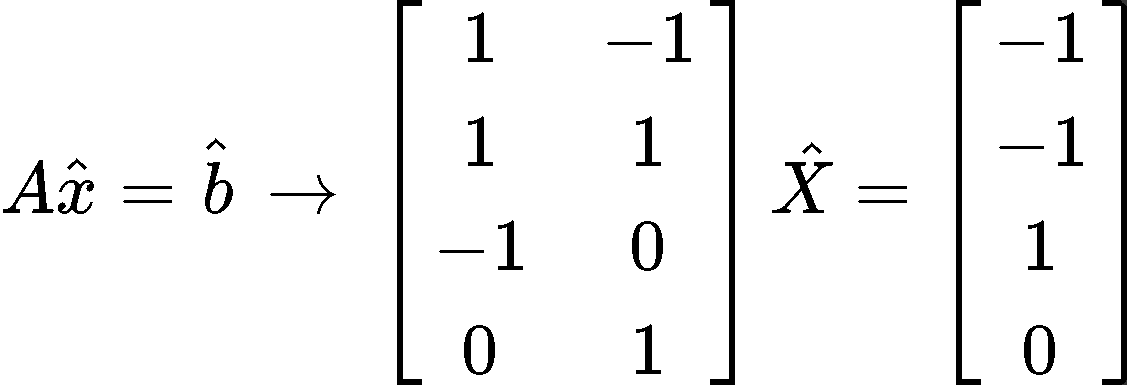
Where we can easily obtain the vector since its components are and, and so:
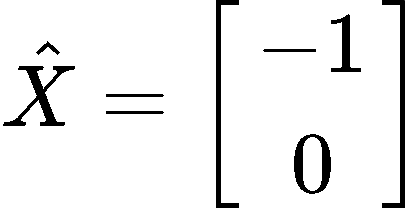
This is it for our lesson on least squares, we hope you enjoyed it, and see you in the next lesson, the final one for this course!
In linear algebra, we have dealt with questions in which does not have a solution. When a solution does not exist, the best thing we can do is to approximate . In this section, we will learn how to find a such that it makes as close as possible to .
If is an matrix and is a vector in , then a least-squares solution of is a in where
For all in .
The smaller the distance, the smaller the error. Thus, the better the approximation. So the smallest distance gives the best approximation for . So we call the best approximation for to be .
The Least-Squares Solution
The set of least-square solutions of matches with the non-empty set of solutions of the matrix equation .
In other words,
→
Where is the least square solutions of .
Keep in mind that is not always a unique solution. However, it is unique if one of the conditions hold:
1. The equation has unique least-squares solution for each b in .
2. The columns of are linearly independent.
3. The matrix is invertible.
The Least-Squares Error
To find the least-squares error of the least-squares solution of , we compute
Alternative Calculations to Least-Squares Solutions
Let be a matrix where are the columns of . If {} form an orthogonal set, then we can find the least-squares solutions using the equation
where
Let be a matrix with linearly independent columns, and let be the factorization of . Then for each in , the equation has a unique least-squares solution where
→
If is an matrix and is a vector in , then a least-squares solution of is a in where
For all in .
The smaller the distance, the smaller the error. Thus, the better the approximation. So the smallest distance gives the best approximation for . So we call the best approximation for to be .
The Least-Squares Solution
The set of least-square solutions of matches with the non-empty set of solutions of the matrix equation .
In other words,
→
Where is the least square solutions of .
Keep in mind that is not always a unique solution. However, it is unique if one of the conditions hold:
1. The equation has unique least-squares solution for each b in .
2. The columns of are linearly independent.
3. The matrix is invertible.
The Least-Squares Error
To find the least-squares error of the least-squares solution of , we compute
Alternative Calculations to Least-Squares Solutions
Let be a matrix where are the columns of . If {} form an orthogonal set, then we can find the least-squares solutions using the equation
where
Let be a matrix with linearly independent columns, and let be the factorization of . Then for each in , the equation has a unique least-squares solution where
→

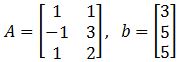
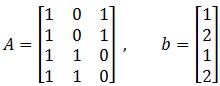
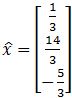 . Compute the least-square error if
. Compute the least-square error if