Sign In
Sign Up
flag-latam

Transformaciones de funciones: Traslaciones horizontales

  1. Introducción0/1 watched
  2. Ejemplos0/2 watched
  1. 0/1
  2. 0/2
Now Playing:Es transformations of functions horizontal translations– Example 0
Introducción
0/1 watched
    • Estudiando traslaciones horizontales
Ejemplos
0/2 watched
  1. Traslaciones horizontales
    1. Dibuja la gráfica de las siguientes funciones en el mismo plano cartesiano:
      y=(x)2y=(x)^{2} \quad vs y=(x−6)2 \quad y=(x-6)^{2} \quad vs y=(x+5)2 \quad y=(x+5)^{2} \quad


    2. Si comparamos con la gráfica de  y=(x)2\, y=(x)^{2}:
      • La gráfica de y=(x−6)2y=(x-6)^{2} se trasladó horizontalmente ____ unidades a la ___________.
      • La gráfica de y=(x+5)2y=(x+5)^{2} se trasladó horizontalmente ____ unidades a la ___________.
    Notación de funciones
    Jump to:Notes
    Notes

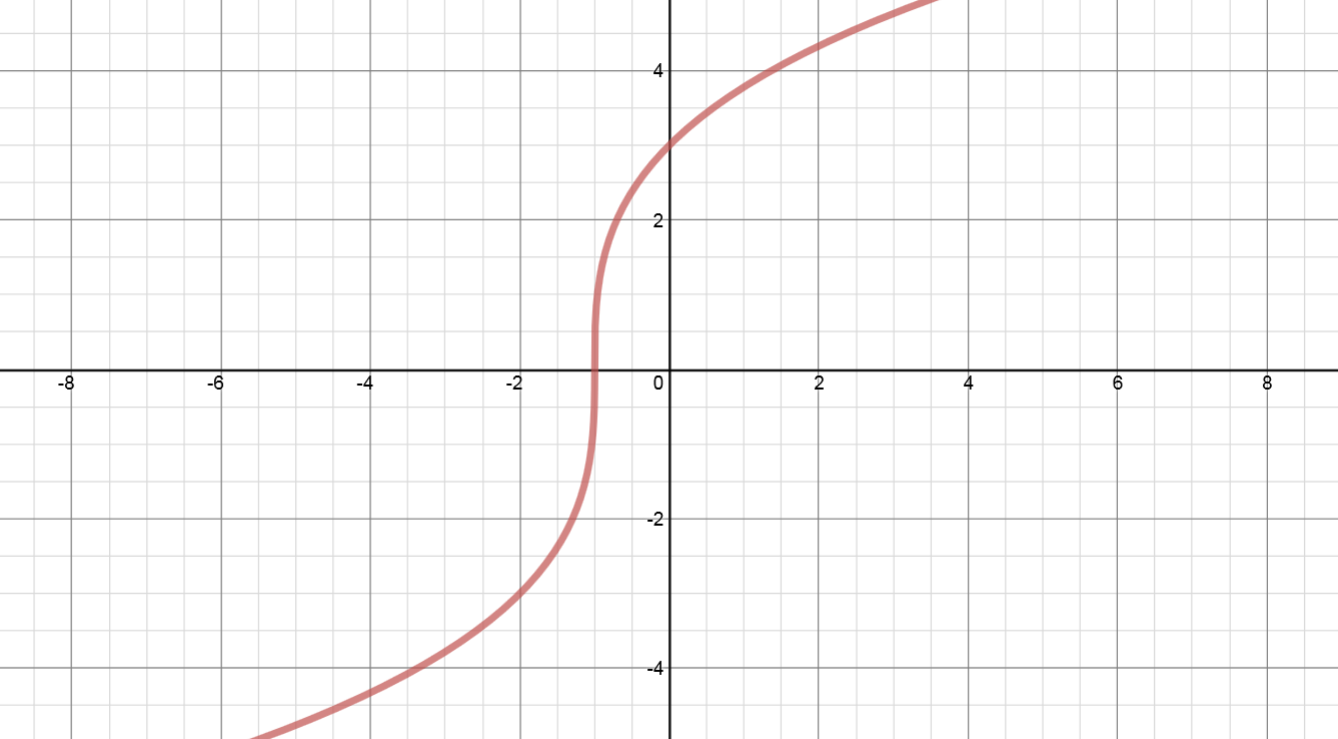
    Una traslación horizontal se refiere al desplazamiento a lo largo del eje xx (hacia la derecha o hacia la izquierda) que se puede producir cuando a la gráfica de una función se le cambian los valores de xx.

    Imagina que tienes una función original y=f(x)y=f(x).
    Para producir una traslación horizontal hacia la izquierda, en lugar de tener una función con respecto a xx, ahora será con respecto a xx más una constante, de manera que tu nueva función sería: y=f(x+c)y=f(x+c).
    Para producir una traslación horizontal hacia la derecha, en lugar de tener una función con respecto a xx, ahora será con respecto a xx menos una constante, de manera que tu nueva función sería: y=f(x−c)y=f(x-c).

    Por ejemplo:
    Si tienes una función original y=f(x)y=f(x) y después se le hace la traslación horizontal que resulta en y=f(x−4)y=f(x-4), esto significa que la función se desplazará 4 unidades hacia la derecha.
    En cambio, si se hace una traslación horizontal que resulta en y=f(x+9)y=f(x+9), la función se desplazará 9 unidades hacia la izquierda.