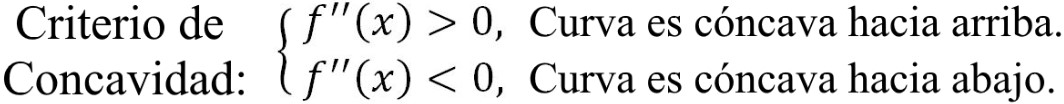En esta sección extenderemos nuestro conocimiento acerca de la conexión entre las derivadas y la forma de una gráfica de una función.
Normas para dibujar las gráficas de funciones y sus derivadas a) Dominio Primero que nada, determina el dominio del a función y encuentra los valores no permitidos de en el caso de funciones racionales. b) Interceptos Encuentra los interceptos en y .
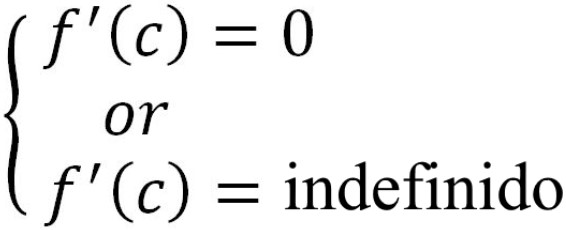
Criterio de concavidad (también llamado la prueba de concavidad o criterio de la segunda derivada):
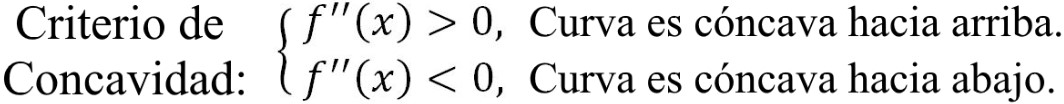
Normas para dibujar las gráficas de funciones y sus derivadas a) Dominio Primero que nada, determina el dominio del a función y encuentra los valores no permitidos de en el caso de funciones racionales. b) Interceptos Encuentra los interceptos en y .
- Para encontrar el intercepto en asigna el valor de cero a y despeja .
- Para encontrar el intercepto en asigna el valor de cero a y despeja .
- Asíntotas verticales: Para funciones racionales, los asíntotas verticales pueden ser encontrados asignando la expresión en el denominador como igual a cero después de haber cancelado los factores comunes.
- Asíntotas horizontales: Evalúa para determinar el comportamiento del extremo derecho; evalúa para determinar el comportamiento del extremo izquierdo.
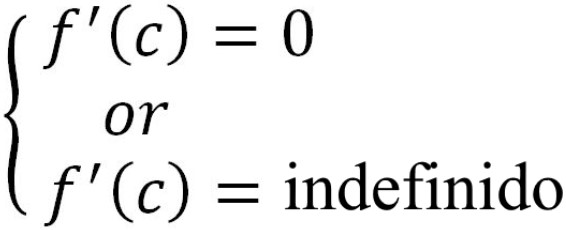
Criterio de concavidad (también llamado la prueba de concavidad o criterio de la segunda derivada):