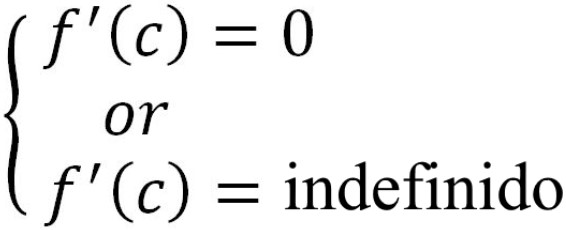Sign In
Sign Up
flag-latam

Puntos críticos, máximos y mínimos

  1. Introducción0/2 watched
  1. 0/2
Now Playing:Es critical number and maximum and minimum values – Example 0a
Introducción
0/2 watched
  1. ¿Cómo se describen las gráficas de las funciones?
    describe a graph of function, the critical number & maximum and minimum values
  2. ¿Cómo se describen las gráficas de las funciones?
    describe a graph of function, the critical number & maximum and minimum values

    ∙\bullet Máximo relativo (local)
    ∙\bullet Mínimo relativo (local)
    ∙\bullet Punto crítico
  3. ¿Cómo se describen las gráficas de las funciones?
    describe a graph of function, the critical number & maximum and minimum values

    En el intervalo
    −1≤x≤12 -1\leq x\leq 12\, define:
    ∙\bullet Máximo absoluto
    ∙\bullet Mínimo absoluto
Posición, velocidad y aceleración
Jump to:Notes
Notes
Otro uso poderoso del cálculo diferencial es la optimización de funciones, por ejemplo:
Encontrar el número de productos que se necesita vender en una tienda para maximizar su ganancia mensual o para minimizar el costo al mes.

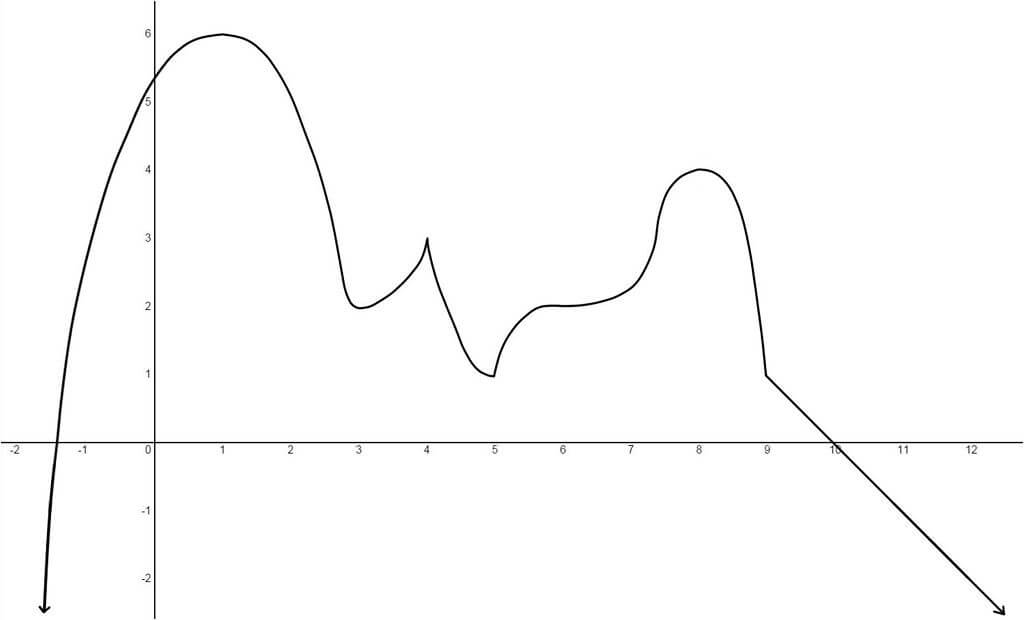
En esta sección veremos la relación entre el cálculo diferencial y el encontrar los extremos de una función: el punto crítico, el máximo y el mínimo.

Número crítico: Valor  c\ c en el dominio de la función  f\ f tal que:

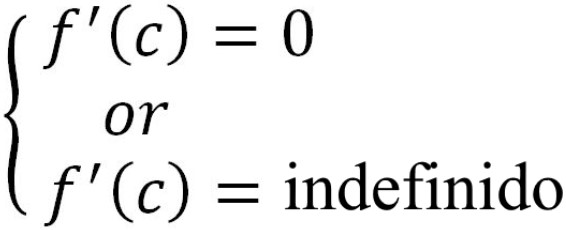
Puntos críticos, máximos y mínimos