Estimating decimals
Topic Notes
In this lesson, we will learn:
- How to use number lines to help estimate decimal values (to the closest whole number or closest tenth)
- How to round decimal numbers to the nearest whole number, or the nearest tenth
Notes:
- To estimate means to roughly guess the value (or a rough calculation)
- For estimating decimals, have less decimal place values in your number
- Rounding is one strategy for estimation; by making numbers less exact (less precise), they become simpler or easier to do math with
- We use the symbol meaning "about equal to" for estimation and rounding
- Ex. 39 is about equal to the even number 40; 39 40
- We can use number lines to help estimate decimal values
- Find the closest distance to the nearest whole number OR the nearest tenth
- Ex. rounding 0.3 to the nearest whole number, is it closer to 0 or 1?

- 0.3 is closer to 0 than it is to 1. Therefore, 0.3 0
- Ex. rounding 0.66 to the nearest tenth, is it closer to 0.6 or 0.7?

- 0.66 is closer to 7 than it is to 6. Therefore, 0.66 0.7
- The steps for rounding numbers:
- Look at the place value you are rounding to ("target").
start writing a new rounded number, where:
any smaller place values (to the right) can be changed to zero
any bigger place values (to the left) can be kept - Look at the place value to the right of where you are rounding to.
- if the digit is , round up (increase the target by 1)
- if the digit is < 5, round down (keep the target the same)
- Any trailing zeroes in decimals can be removed (i.e. 0.50 = 0.5; 2.0 = 2)
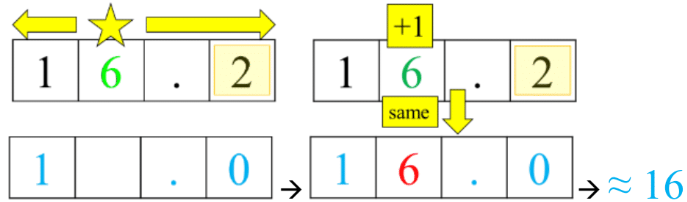
- When your target digit is 9, if you round up then you will regroup to the next place value up.
- Ex. Rounding 0.97 to nearest tenth round up from 0.9 to 1.0; 0.97 1.0

