Sign In
Sign Up
flag-ie

Mastering Triple Integrals in Spherical Coordinates
Unlock the power of 3D integration with spherical coordinates. Learn to solve complex problems in physics and engineering, and elevate your calculus skills to new heights.

  1. Intros0/3 watched
  2. Examples0/4 watched
  1. 0/3
  2. 0/4
Now Playing:Triple integrals in spherical coordinates – Example 0a
Intros
0/3 watched
  1. Triple Integrals in Spherical Coordinates Overview:
  2. Triple Integrals in Spherical Coordinates Overview:
    Spherical Coordinates
    • (x,y,z)→(ρ,θ,φ)(x,y,z) \to (\rho, \theta, \varphi )
    • Graph of the coordinates in 3D
  3. Triple Integrals in Spherical Coordinates Overview:
    Equations to Convert from Cartesian to Spherical
    • Pythagoras
    • Trig Ratios
Examples
0/4 watched
  1. Convert the following integral into spherical coordinates

    ∫−3232∫−94−x294−x2∫3x2+3y29−x2−y2 x3+xy2+xz2 dz dy dx\large \int_{-\frac{3}{2}}^{\frac{3}{2}}\int_{-\sqrt{\frac{9}{4}} - x^{2}}^{\sqrt{\frac{9}{4} - x^{2}}}\int_{\sqrt{3x^{2} + 3y^{2}}}^{\sqrt{9 - x^{2} - y^{2}}} \, x^{3} + xy^{2} + xz^{2} \,dz \,dy \,dx
    Double integrals over a rectangular region
    Jump to:NotesConceptFAQsPrerequisites
    Notes
    Notes:

    Spherical Coordinates

    There are times where instead of Cartesian coordinates, we use spherical coordinates for triple integrals. For spherical coordinates, instead of x,y,zx,y,z's, we have ρ,θ,φ\rho, \theta, \varphi's. In other words,

    (x,y,z)→(ρ,θ,φ)(x,y,z) \to (\rho, \theta, \varphi )

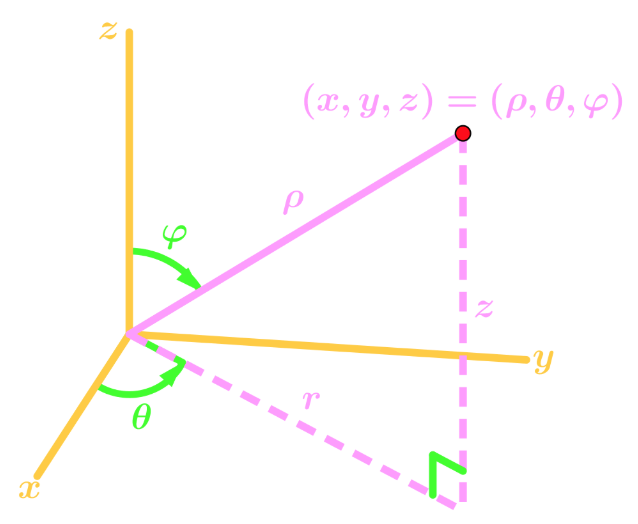
    spherical coordinates

    Equations to Convert From Cartesian to Spherical

    From the graph, we can obtain the following equations which will be useful for converting spherical to cartesian, or vice versa:

    r=ρsin⁡φr = \rho \sin \varphi
    z=ρcos⁡φz = \rho \cos \varphi
    z2+r2=ρ2z^2 + r^2 = \rho^2

    Using the equations from past sections, we can also obtain more equations:

    x=ρsin⁡φcos⁡θx = \rho \sin \varphi \cos \theta
    y=ρsin⁡φsin⁡θy = \rho \sin \varphi \sin \theta
    ρ2=x2+y2+z2\rho^2 = x^2 + y^2 + z^2


    Triple Integrals in Spherical Coordinates

    Suppose we want to convert a triple integral of f(x,y,z)f(x,y,z) in Cartesian Coordinates to spherical Coordinates on region EE. Let region EE be:

    a≤ρ≤b a \leq \rho \leq b
    α≤θ≤β\alpha \leq \theta \leq \beta
    δ≤φ≤γ\delta \leq \varphi \leq \gamma

    Then the conversion would be:

    ∫∫∫Ef(x,y,z)dV=∫δγ∫αβ∫abf(ρsin⁡φcos⁡θ,ρsin⁡φsin⁡θ,ρcos⁡φ)ρ2sin⁡φdpdθdφ\int \int \int_E f(x,y,z)dV = \int_\delta^\gamma \int_\alpha^\beta \int_a^b f(\rho \sin \varphi \cos \theta, \rho \sin \varphi \sin \theta, \rho \cos \varphi)\rho^2 \sin \varphi d p d\theta d\varphi

    Concept

    Introduction to Triple Integrals in Spherical Coordinates

    Triple integrals in spherical coordinates are a powerful tool in multivariable calculus, essential for solving complex three-dimensional problems. This concept extends the idea of double integrals to three dimensions, utilizing spherical coordinates (r, θ, φ) instead of Cartesian coordinates. The introduction video provides a visual representation of how these integrals work, making it easier to grasp this abstract concept. Understanding triple integrals in spherical coordinates is crucial for various applications in physics, engineering, and mathematics. They are particularly useful when dealing with spherically symmetric problems, such as gravitational fields or electric potentials. Mastering this topic allows students to tackle more advanced problems in multivariable calculus and opens doors to understanding higher-dimensional integration techniques. The video demonstration helps clarify the transformation process from Cartesian to spherical coordinates and illustrates how to set up and evaluate these integrals effectively, making it an invaluable resource for students and professionals alike.

    FAQs

    Q1: What are the advantages of using spherical coordinates for triple integrals?
    A1: Spherical coordinates offer several advantages for triple integrals, especially when dealing with spherically symmetric problems. They simplify calculations for objects with radial symmetry, such as spheres or conical shapes. The coordinate system naturally aligns with these geometries, often resulting in simpler integrand expressions and more intuitive limits of integration. This can lead to more efficient problem-solving in fields like physics, engineering, and astrophysics.

    Q2: How do you convert from Cartesian to spherical coordinates?
    A2: To convert from Cartesian (x, y, z) to spherical (ρ, θ, φ) coordinates, use these formulas: ρ = (x² + y² + z²) θ = arctan(y/x) φ = arccos(z/ρ) Remember that ρ represents the distance from the origin, θ is the azimuthal angle in the xy-plane, and φ is the polar angle from the z-axis.

    Q3: Why is the Jacobian determinant important in spherical coordinate transformations?
    A3: The Jacobian determinant (ρ² sin φ) is crucial when converting triple integrals to spherical coordinates. It accounts for the change in volume element from Cartesian to spherical coordinates. Without including this factor, the integral would not accurately represent the volume or quantity being measured. The Jacobian ensures that the integral's value remains consistent across different coordinate systems.

    Q4: What types of problems are best suited for spherical coordinates?
    A4: Spherical coordinates are ideal for problems involving spherical symmetry or radial dependence. This includes calculating gravitational or electric fields around spherical objects, analyzing fluid flow around spheres, studying planetary atmospheres, and solving problems in astrophysics. They're also useful in engineering applications like antenna design and stress analysis in spherical structures.

    Q5: How can I improve my skills in solving triple integrals using spherical coordinates?
    A5: To improve your skills, practice regularly with a variety of problems. Start with simple spherical shells and gradually move to more complex shapes. Focus on visualizing 3D objects and setting up correct integration limits. Review trigonometric identities and practice applying them in spherical coordinate problems. Utilize online resources, textbooks, and study groups. Don't hesitate to seek help from instructors or tutors when needed. Remember, mastery comes with consistent practice and patience.

    Prerequisites

    Understanding the foundation of advanced mathematical concepts is crucial for mastering complex topics like triple integrals in spherical coordinates. One of the key prerequisite topics that plays a significant role in this area is integration using trigonometric identities. This fundamental skill is essential for navigating the intricate world of triple integrals in spherical coordinates.

    When dealing with triple integrals in spherical coordinates, students often encounter complex expressions involving trigonometric functions. The ability to manipulate and integrate these functions efficiently is where the knowledge of integration using trigonometric identities becomes invaluable. This prerequisite topic equips students with the tools to simplify and solve intricate integrals that arise in spherical coordinate systems.

    Trigonometric identities serve as a bridge between the familiar Cartesian coordinate system and the more specialized spherical coordinate system. As students transition to working with triple integrals in spherical coordinates, they'll find that many of the integrands involve sine and cosine functions. The techniques learned in integration using trigonometric identities become crucial for evaluating these complex expressions accurately.

    Moreover, the transformation between coordinate systems often requires a solid understanding of trigonometric relationships. Students who have mastered integration using trigonometric identities will find it easier to grasp the concept of Jacobian determinants, which are essential when changing variables in multiple integrals. This prerequisite knowledge helps in understanding how volume elements transform from Cartesian to spherical coordinates.

    Another aspect where trigonometric identities prove useful is in simplifying the limits of integration in spherical coordinates. Often, the bounds of a triple integral in spherical form involve trigonometric functions. Being adept at manipulating these functions allows students to set up the integral correctly and identify the appropriate limits of integration.

    Furthermore, many real-world applications of triple integrals in spherical coordinates, such as calculating gravitational fields or electric potentials, involve expressions that are best handled using trigonometric identities. Students who are comfortable with these identities will find it easier to tackle practical problems and understand their physical significance.

    In conclusion, mastering integration using trigonometric identities is not just a stepping stone but a fundamental pillar in understanding and applying triple integrals in spherical coordinates. It provides the necessary mathematical dexterity to handle complex integrations, coordinate transformations, and real-world applications. By solidifying this prerequisite knowledge, students set themselves up for success in navigating the challenging yet rewarding world of advanced calculus and multivariable integration.