Notation for a Limit of 2 Variable Functions Suppose we want to take the limit of and of f(x,y). Then we write this notation as:
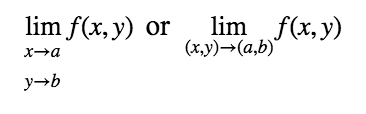
In a sense, we are trying to approach to the point in the function without being at that point.
Limit of Continuous 2 Variable Functions
A function is continuous at , then:
In other words, if the function is continuous at , then plug in and to evaluate the limit!
Ways to see if it is continuous at :- Plug into the function and see if the value is undefined. If it is not undefined, then it is continuous.
- If the function has a denominator, plug into the denominator and see if it gives 0. If it is not 0, then the function is continuous.
Visualizing the Limit
There are many paths to approaching a specific point. For example, look at this graph:
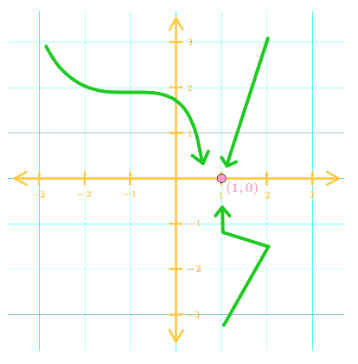
There are an infinite number of paths into approaching the point .
One thing to note: If all paths lead to the same value, then the limit is equal to that value.
What if the Function is Discontinuous at (a,b)?
You want to take different paths to and see if the limits are different. For example, one path can be and the other path can be . If evaluating these paths with limits give different values, then the limit does not exist! We will show an example of this in the video.






