3-Dimensional lines

Notes:

Vector Equation for 3-Dimensional Lines
Unlike 2D lines which have the equation $y=mx+b$, 3-Dimensional lines can be expressed as vector functions in the form

$\vec{r(t)} = \vec{r_0} + \vec{tv} = \lt x_0, y_0, z_0 \gt + \; t \lt a,b,c \gt$

where t is a variable. Here is the visual representation of the vector $\vec{r(t)}$.

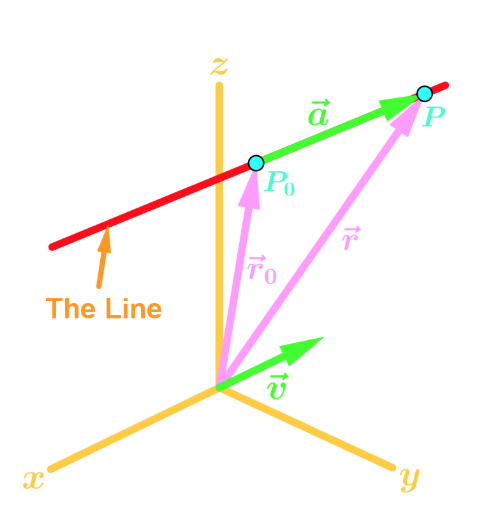
There are 2 other alternate ways to express a 3-Dimensional line.

Parametric Equation
From the equation above, we can rearrange the vector equation so that:

$\vec{r(t)} = \lt x_0,y_0,z_0 \gt + \;t\lt a,b,c \gt$
$\lt x,y,z \gt = \lt x_0, y_0, z_0 \gt + \lt ta,tb,tc \gt$
$= \lt x_0 + ta, y_0 + tb , z_0 + tc \gt$

Then we can see that:

$x = x_0 + ta$
$y = y_0 + tb$
$z = z_0 + tc$

Hence these set of equations of the Parametric Equation of the equation of the 3D line.

Symmetric Equations Assume that $a,b,c$ are non-zero. Then rearranging the set of equations from above gives us:

$x = x_0 + ta \to x - x_0 = ta \to \frac{x-x_0}{a} = t$
$y = y_0 + tb \to y - y_0 = tb \to \to \frac{y-y_0}{b} = t$
$z = z_0 + tc \to z - z_0 = tc \to \frac{z-z_0}{c} = t$

Hence we have our symmetric equation of the equation of the 3D line:

$\frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c}$