Factorial notation
What is a factorial?
A factorial is the multiplication of a number with all of those positive numbers below it. In other words, when you want to compute the factorial of a number, you multiply this number times all of the numbers smaller than it up to 1.
This up to 1 is very important since the factorial of a negative number does not exist, and the factorial of 0 is defined as 1. Therefore, the numbers in a factorial are all positive integers. Consequently, the formal factorial definition says that a factorial is the product of a positive integer with all the consecutive positive integers that have a lower value than itself.
Mathematically speaking, the factorial of a number is defined as:
And so, the factorial notation of a number is done just by applying an exclamation mark to its right. Something important to remember is that since the 0 factorial is defined as 1 (0! = 1), then it means that the zero factorial is equal to the factorial of 1.
Combinatorics problems using factorials
On the next examples we will get to see how is that the factorial notation of a multiplication is useful when working in combinatorics problems.
Example 1
How many ways are there to arrange 4 different books side by side on a bookshelf?For this case we have four different books which we will define as a math book, a physics book, a chemistry book and a history book. And so, the setting is that we have four books that can be arranged in four different positions side by side as seen in the next figure:
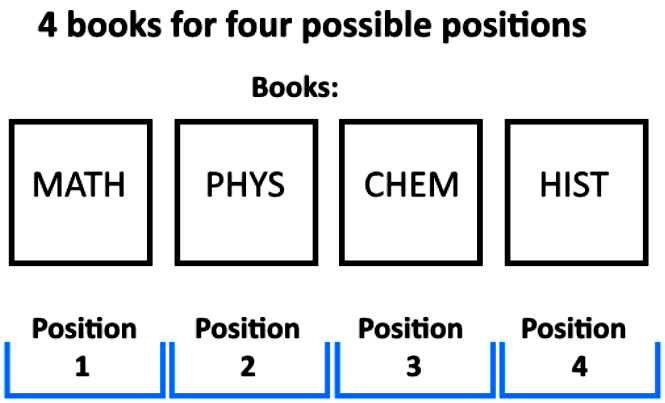
If you think about it, the first position has 4 different books as a possibility to be there, and we can pick any of them. And so, we pick one book from the four to be in the first position, and continue to the next position. For the second position, we are left with 3 possible books, we pick one and continue to the next position; on the third position we have 2 possible books left, we pick one and continue; in the last position (4th position) we have only one book left that can be there, and so our arrangement and the process we just explained can be seen in the next figure:
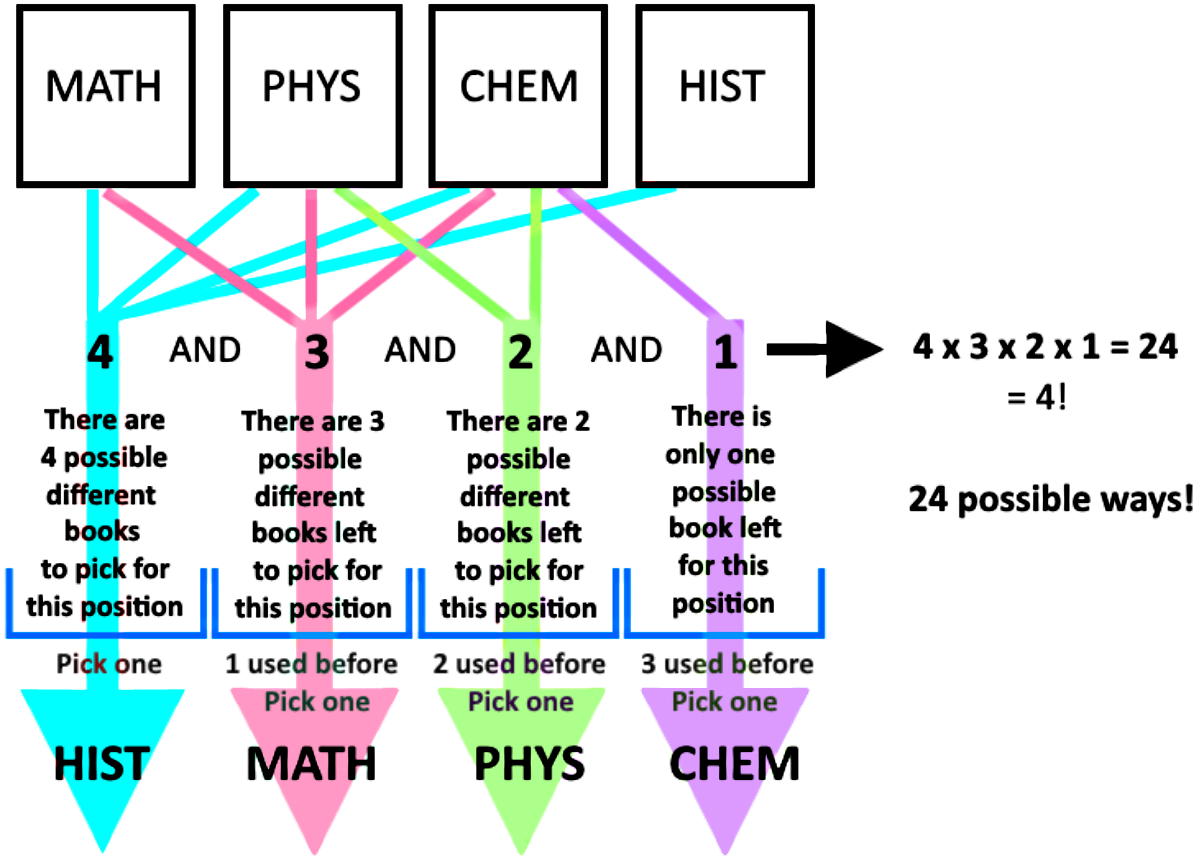
Thus, following the fundamental counting principle we know that we have to multiply the possible outcomes of each category to obtain a total of 24 possible ways in which the books can be arranged.
If you notice, the multiplication resulted from the application of the fundamental counting principle is the same as the factorial of four! And so, we can clearly see how the factorial notation has been designed to help us out in abbreviating what can get to be a large multiplication into a simple expression such as: 4!
Example 2
Using what we have learned of factorial notation:And (zero factorial) by definition.
a) Evaluate: 5!
This problem is very simple, you just have to compute the multiplication required to obtain the factorial of 5, using the factorial formula depicted in equation 1 we have that:
b) Evaluate:
On this case you will see that when dividing factorials, if the factorial in the numerator is bigger than the one in the denominator, several of the factors above will be cancelled with those below and you can simplify the operation by computing the multiplication of the factors left:
c) Simplify:
Another example of a factorial being divided by a smaller one. Notice how the factorial in the denominator cancels out most of the factors in the factorial above, and so, the expression gets simplified:
d) Simplify:
On this case we have two factorials dividing each other, but the highest one is found in the denominator, which means that it will cancel the factors contained in the numerator to produce an expression such as:
e) Simplify:
For this case we combine what we have seen in parts c) and d) since this particular division of factorials includes multiplication of factorials in both the numerator and denominator. Therefore, you can factor out the whole expression into two divisions of factorials being multiplied.
This particular operation can be done in many ways, let us show you one of them (you can practice at home by working the operations in different order).
f) Solve:
In order to solve this particular factorial equation we pass the 3 factorial in the denominator to the other side of the equation by multiplying it in both sides, and so:
And now, we can just simplify the division of factorials on the left hand side in the same way as we have done it before:
Once the division of factorials has been simplified we obtain the next quadratic equation:
With this, we can use the quadratic formula and solve for . Since the quadratic formula is defined as:
On this case we have that
Therefore we solve for n in the following manner:
Since the factorial of negative numbers does not exist, and the original expression to solve in this problem contains a term of in the numerator, must be equal to 7; putting = -6 would mean that we would have a (-6)! term in the numerator of the original expression, which is undefined! Therefore the answer is = 7
Example 3
In this example we take a look at the arrangement of letters in a word "without repetitions", which means to compute the , where equals the number of letters in the word.This process is the same that what we saw in the first example with the 4 different books being arranged side by side, you cannot repeat a book, just as in here the condition is that you do not repeat a letter. With all of this in mind, determine the number of different arrangements of all the letters in the following words:
a) DOG
Total amount of letters = 3, therefore = 3, and the total amount of different positions in which these letters can be arranged is equal to 3! = (3)(2)(1) = 6
b) MATH
Total amount of letters = 4, therefore = 4, and the total amount of different positions in which these letters can be arranged is equal to 4! = (4)(3)(2)(1) = 24
c) COMPUTER
Total amount of letters = 8, therefore = 8, and the total amount of different positions in which these letters can be arranged is equal to 8! = (8)(7)(6)(5)(4)(3)(2)(1) = 40,320
These examples were simple because these are words which have all distinct letters (without repetition), meaning that you can simply use the factorial of the amount of letters that you have in each case to obtain the different ways in which you can arrange them. The next example represents a case in which the words contain repeated letters, see how the difficulty level rises:
Example 4
On this example we take a look at the arrangement of letters in a word "with repetitions", which means that letters within the given word are not all distinct.The equation that produces the total amount of ways in which the letters of these words with repetitions can be arranged goes as:
Where equals the total number of letters in the word, and the repetitions mean how many times a letter repeats itself. For example if you have 5 letters and one repeats 3 times, then you would have that = 5 and the first repetition is 3! (there are no more repetitions in this case, and so, the equation for the arrangements would be simply: 5!/3!.
With that in mind, determine the number of different arrangements of all the letters in the following words:
a) ABC vs ABB
In this case, both ABC and ABB have = 3, therefore, for ABC we simply have that:
For ABB we have that the letter B repeats twice, and so:
b) Canada
The total arrangements possible with the letters in the word Canada are calculated as follows (where = 6):
c) BANANA
For this case =6 and you have two repetitions, letter N repeats twice, and letter A repeats trice; therefore:
d) REPETITION
For this case = 10 and you have three repetitions: the letters E, T and I repeat twice each, therefore:
Example 5
For this problem example we will be taking a look at arrangement with restrictions, meaning that even when you have a word with all distinct letters, there may be certain conditions imposed on the arrangements of its words and so, these conditions (or restrictions) must be dealt with first.Determine the number of different arrangements of all the letters in the word: COMPUTER
1. if there are no restrictions
In this case, we do not have repetitions and no restrictions, therefore, the arrangements are easy to calculate: just calculate factorial products for the total number of letters in the word. Since there are 8 letters in the word computer, then the total possible arrangements are 8! = 40,320.
2. if the vowels must be together
We have 3 vowels (O, U and E) in the word COMPUTER, and our restriction for this case is that all of them will be written together. So how many arrangements of the word meet this restriction?
Let us think on the word COMPUTER, take the three vowels out: O,U,E and think of them as a single unit to have: C, M, P, T, R, {O, U, E} as the six components of the word.
Then, we use the same logic used in example one (about arranging books in different order side by side) and think of the letters in the word computer as a unit (just like each book in example one) to be arranged in different positions side by side, except for the vowels which are all merged together in a single unit. Look at the next figure to see what we are talking about:
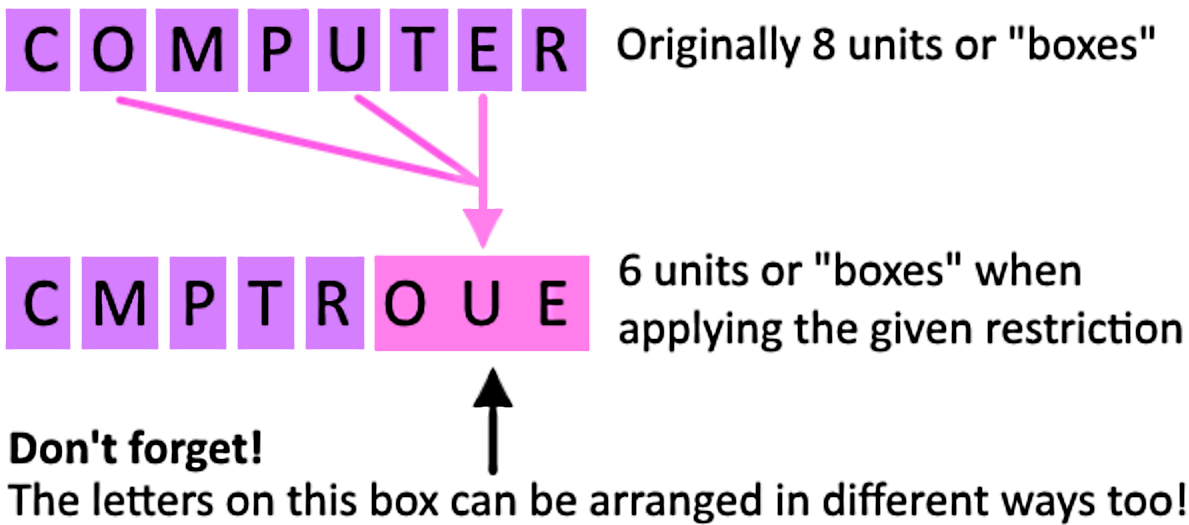
So, in this case in order to obtain the total amount of different arrangements that can happen when applying the given restriction (having all the vowels together) can be obtained by calculating the different ways in which the six boxes can be arranged, times the different ways in which the vowels can be arranged within their box. Therefore:
Where 6! In equation 18 represents the total amount of arrangements of the 6 boxes, and 3! Represents the total amount of arrangements the vowels can have within their own box.
On the videos for this lesson you will find a few more examples on this topic, so dont forget to watch all of the video lessons.
To finalize this lesson we recommend you to visit the next article on factorials which contains a few examples and a different arrangement on how the factorial product is written (remember the order of the factors does not alter the product in a multiplication, and so, a factorial product can be written in different orders).
This is it for our lesson of today, see you in the next one!






