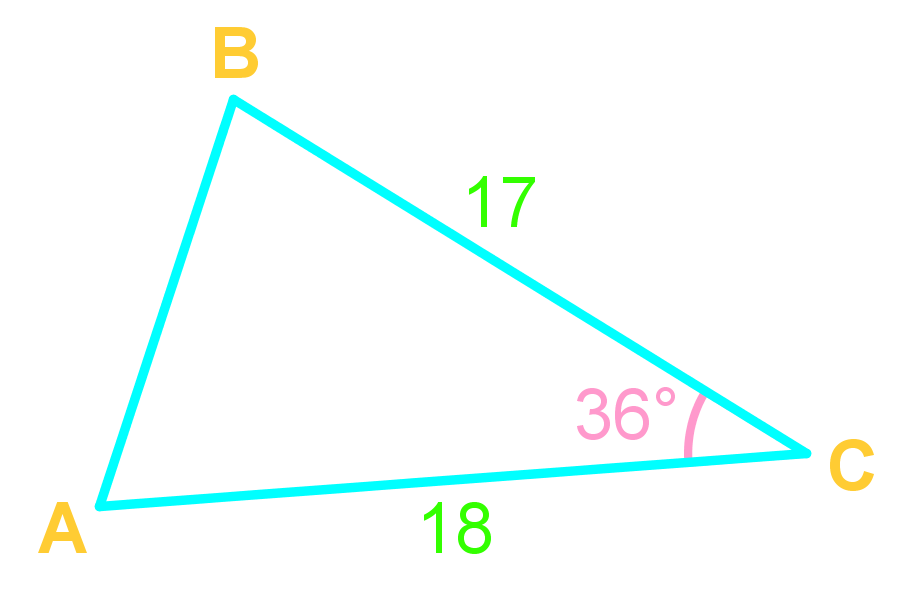
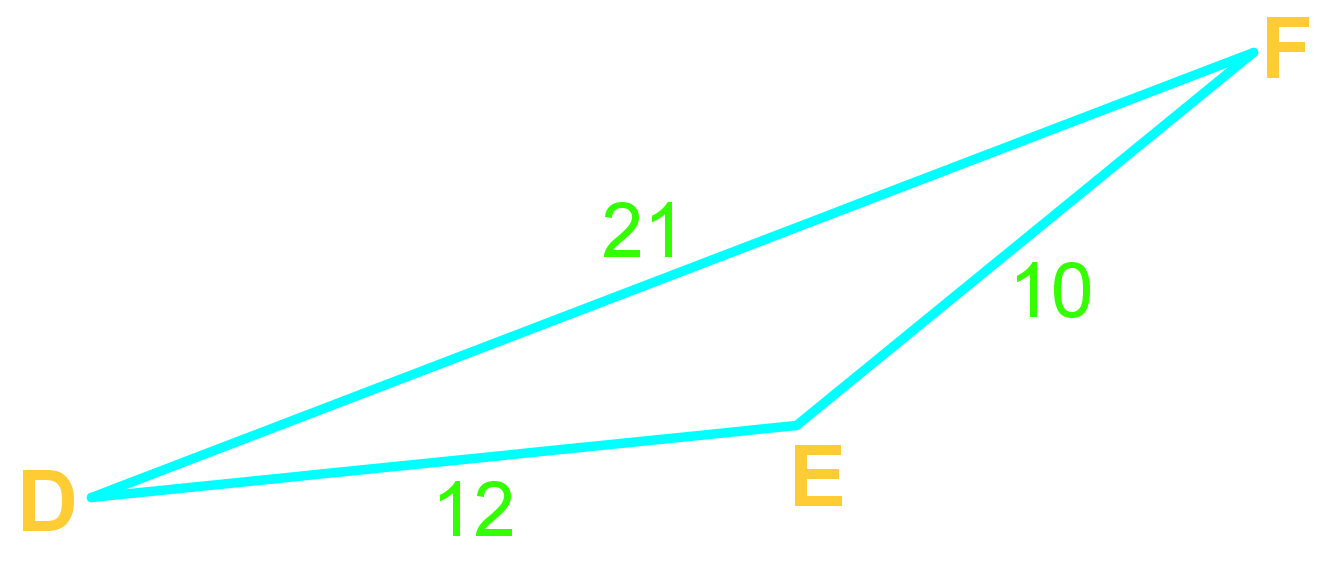
Use the Law of Cosine when given SSS (all sides), or SAS (angle-sandwich!)
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Use the Law of Cosine when given SSS (all sides), or SAS (angle-sandwich!)
Introduction to the Law of Cosines
The Law of Cosines is a fundamental theorem in trigonometry that extends the Pythagorean theorem extension to any triangle. Our introduction video provides a clear and concise explanation of this important concept, making it easier for students to grasp its significance in triangle solving. The Law of Cosines is particularly useful when dealing with oblique triangles, where the Law of Sines falls short. It allows us to find unknown sides and angles in a triangle when we have information about two sides and the included angle (SAS) or all three sides (SSS). This versatility makes it an essential tool in various fields, including physics, engineering, and navigation. By understanding the Law of Cosines, students can tackle more complex geometric problems and gain a deeper appreciation for the interconnectedness of mathematical concepts. The video demonstration helps visualize the application of this law, making it more accessible and memorable for learners.
The Law of Cosines is a powerful extension of the Pythagorean theorem extension, providing a method to solve for unknown sides and angles in any triangle. This is particularly useful in triangle solving scenarios where traditional methods fall short. Understanding how to apply this law can greatly enhance a student's ability to solve complex problems in trigonometry and beyond. The ability to find unknown sides and angles in various contexts makes the Law of Cosines an invaluable tool in both academic and real-world applications.
-
When should the Law of Cosines be used?
The Law of Cosines should be used in two main scenarios: 1) When you know two sides and the included angle (SAS) of a triangle and need to find the third side or remaining angles. 2) When you know all three sides (SSS) of a triangle and need to find any of the angles. It's particularly useful for non-right triangles where the Pythagorean theorem doesn't apply.
-
In what cases do you use the Law of Cosines?
You use the Law of Cosines in cases where you have either SAS (Side-Angle-Side) or SSS (Side-Side-Side) information about a triangle. It's especially helpful when dealing with oblique triangles (non-right triangles) and when you need to find either a missing side length or an angle measure.
-
Where can the Law of Cosines be used in real-world applications?
The Law of Cosines has numerous real-world applications, including: 1) Surveying and land measurement, 2) Navigation in maritime and aviation, 3) Physics problems involving vector analysis, 4) Structural engineering for calculating forces, 5) Robotics and computer vision for spatial reasoning, and 6) GPS technology for triangulation and location determination.
-
Why would you use the Law of Cosines instead of the Law of Sines?
You would use the Law of Cosines instead of the Law of Sines when: 1) You have SAS or SSS information about a triangle, which the Law of Sines can't handle directly. 2) You need to avoid the ambiguous case that can occur with the Law of Sines in SSA situations. 3) You're dealing with problems that require relating all three sides of a triangle simultaneously, which the Law of Cosines does more efficiently.
-
How does the Law of Cosines relate to the Pythagorean theorem?
The Law of Cosines is a generalization of the Pythagorean theorem. In a right triangle, where one angle is 90 degrees (and thus its cosine is 0), the Law of Cosines simplifies to c² = a² + b², which is the Pythagorean theorem. This relationship shows that the Law of Cosines extends the principles of the Pythagorean theorem to all triangles, not just right triangles, making it a more versatile tool in trigonometry.
Mastering the Law of Cosines requires a solid foundation in several key mathematical concepts. One of the most crucial prerequisites is understanding the applications of the Pythagorean theorem. This fundamental principle serves as a stepping stone to more advanced trigonometric concepts, including the Law of Cosines, which can be seen as an extension of the Pythagorean theorem to non-right triangles.
Another essential prerequisite is the ability to use the cosine ratio to calculate angles and sides of triangles. This skill is directly applicable to the Law of Cosines, as it forms the basis for understanding how cosine functions relate to triangle measurements. Similarly, knowing how to use the sine ratio to calculate angles and sides is equally important. These trigonometric ratios are fundamental in solving oblique triangles, which is precisely what the Law of Cosines allows us to do.
Furthermore, familiarity with word problems relating to angles in trigonometry is crucial for applying the Law of Cosines to real-world situations. This prerequisite helps students understand how to interpret problem statements and translate them into mathematical equations using the Law of Cosines.
The Law of Cosines builds upon these foundational concepts, extending our ability to solve triangles beyond the limitations of right-angle trigonometry. It allows us to find unknown sides or angles in any triangle, given three pieces of information about the triangle (provided at least one of them is a side length). This makes it an invaluable tool in various fields, including physics, engineering, and navigation.
Understanding the Pythagorean theorem's applications provides the conceptual framework for grasping how the Law of Cosines works. It helps students see how this law generalizes the Pythagorean theorem, making it applicable to all triangles, not just right triangles. The cosine and sine ratios, which students learn in basic trigonometry, are directly incorporated into the Law of Cosines formula, making proficiency in these ratios essential for both understanding and applying the law.
Moreover, experience with angle-related word problems in trigonometry prepares students to recognize situations where the Law of Cosines is applicable. It develops their problem-solving skills and ability to visualize geometric relationships, which are crucial when working with complex triangular scenarios that the Law of Cosines is designed to solve.
In conclusion, a strong grasp of these prerequisite topics not only facilitates learning the Law of Cosines but also enhances overall mathematical reasoning and problem-solving abilities. By building on these foundational concepts, students can more easily understand, apply, and appreciate the power and versatility of the Law of Cosines in various mathematical and real-world contexts.