Introduction to Inscribed Angles and Central Angles
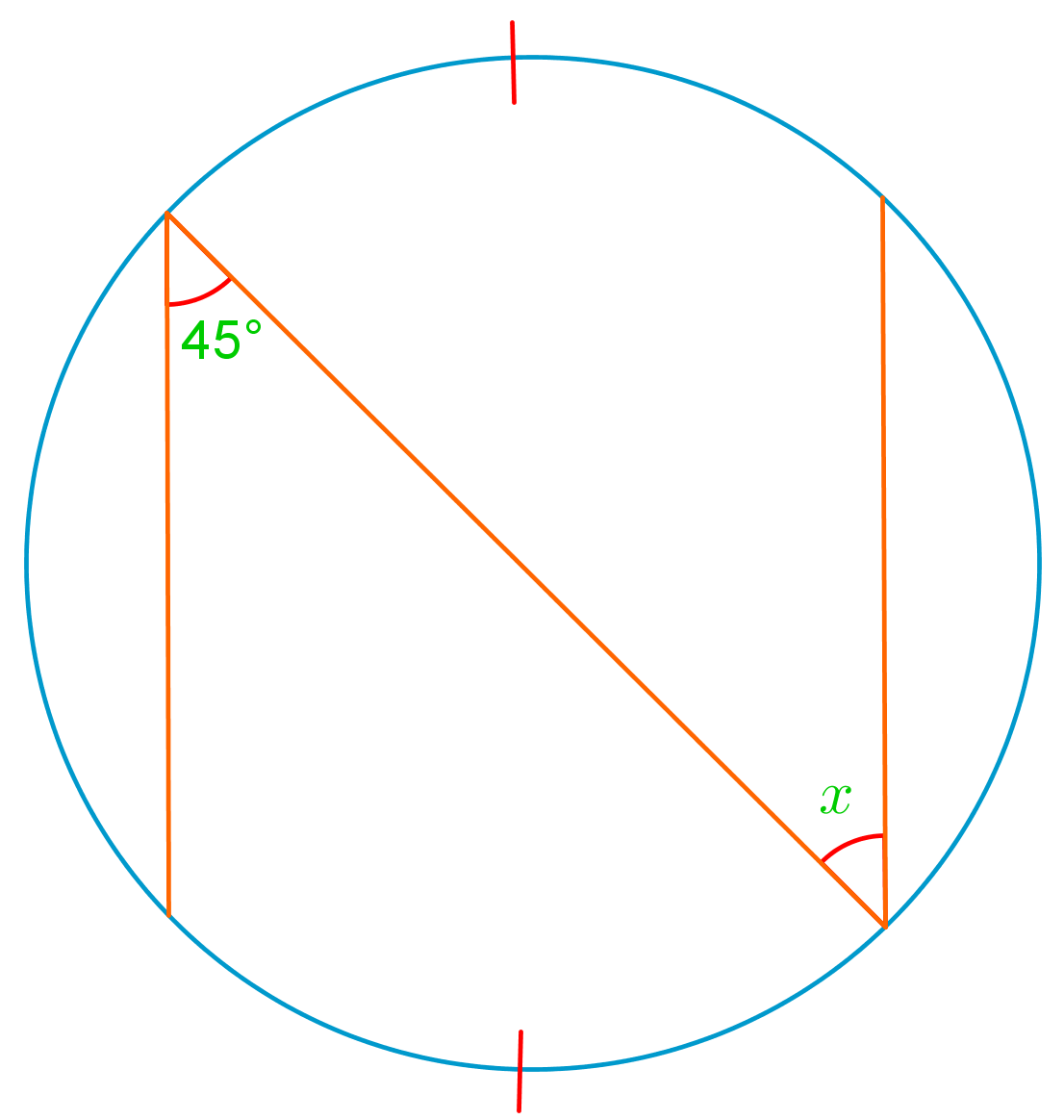
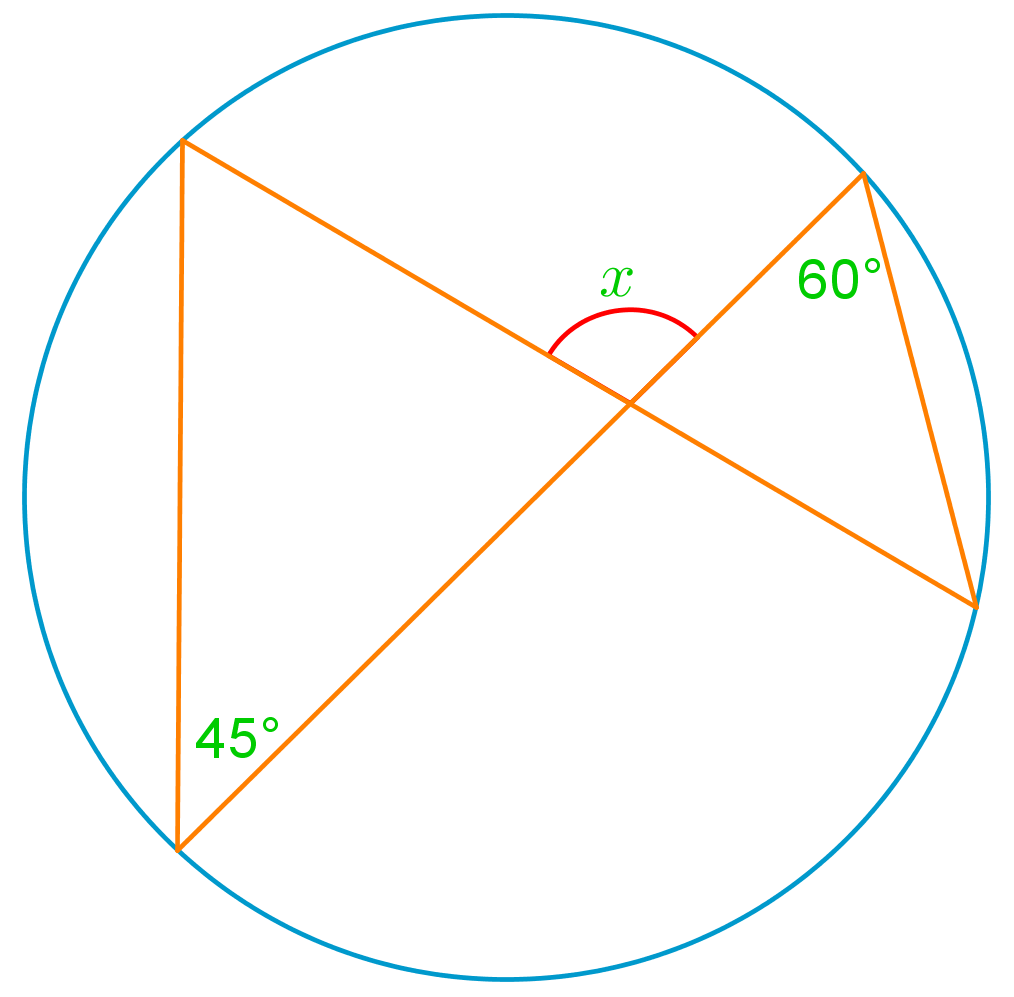
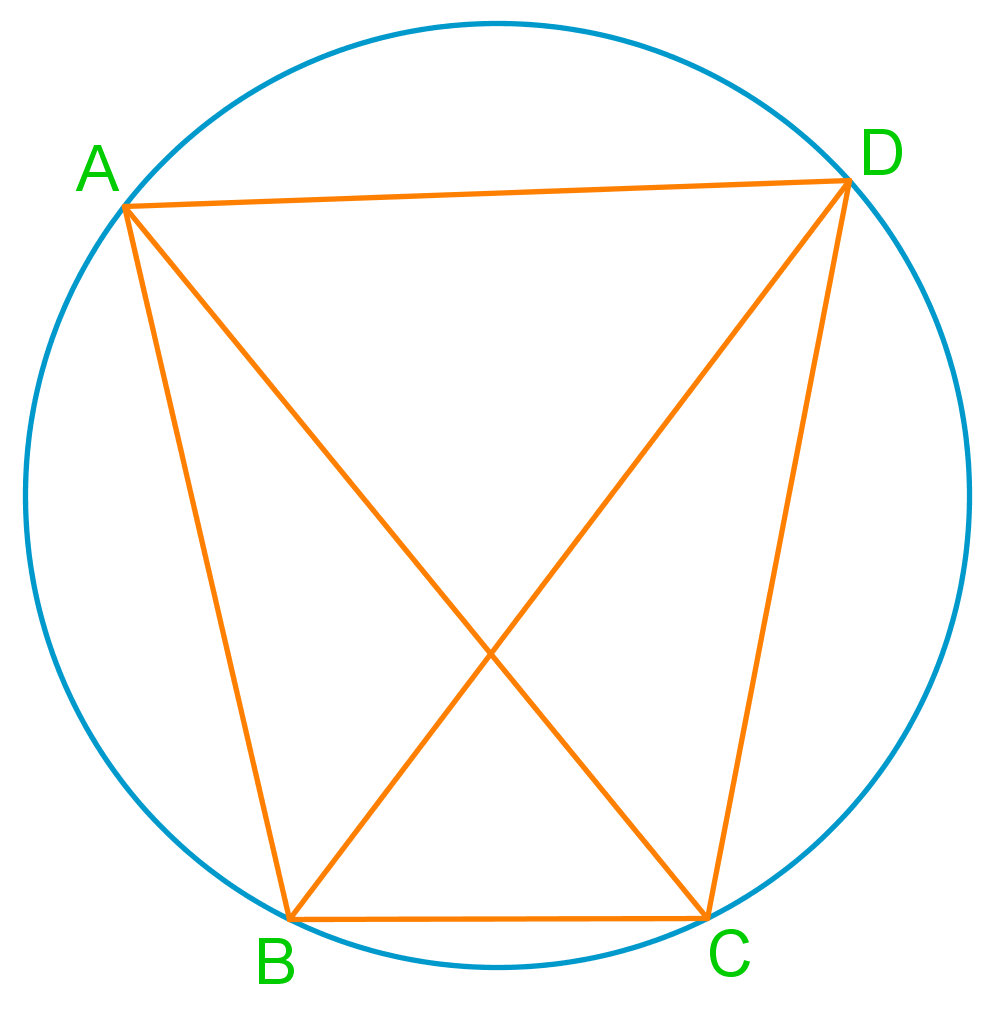
Welcome to our exploration of inscribed angles and central angles in circles! These fundamental geometric concepts are crucial for understanding circle properties and solving various problems in geometry. An inscribed angle is formed when two chords intersect on the circle's circumference, while a central angle has its vertex at the circle's center. The relationship between these angles is fascinating and forms the basis for many geometric theorems. Our introduction video provides a clear, visual explanation of these concepts, making it easier for you to grasp their significance. As we delve deeper into circles, you'll discover how inscribed and central angles relate to arc measures and chord lengths. This knowledge is not only essential for geometry but also has practical applications in fields like engineering and architecture. So, let's embark on this exciting journey through circular geometry together, unraveling the mysteries of inscribed and central angles!