Sign In
Sign Up
flag-us

Mastering Congruence and Congruent Triangles
Dive into the world of congruent triangles and unlock the power of geometry. Learn essential proofs, develop problem-solving skills, and discover real-world applications in this comprehensive lesson.

  1. Intros0/1 watched
  2. Examples0/13 watched
  1. 0/1
  2. 0/13
Now Playing:Congruence and congruent triangles – Example 0a
Intros
0/1 watched
    1. Similar tirangles VS. Congruent triangles
    2. Ways to prove congruency:
      • SSS
      • SAS
      • ASA
      • AAS
Examples
0/13 watched
  1. Which pairs of triangles are congruent?

    1. Congruence and congruent triangles


    2. Determining congruence by examining the angles in the triangle


    3. congruent triangles with equal sides and angles

Pythagorean theorem
Jump to:NotesConceptExampleFAQsPrerequisites
Notes
Concept

Introduction to Congruence and Congruent Triangles

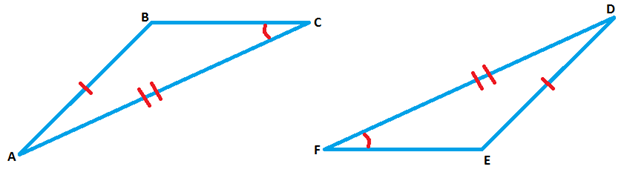
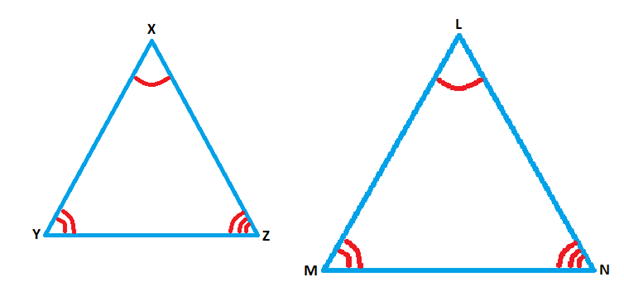
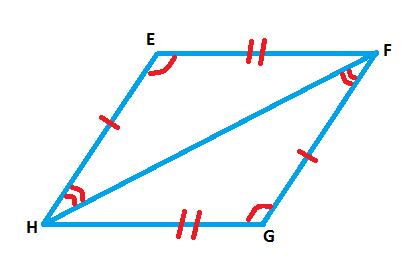
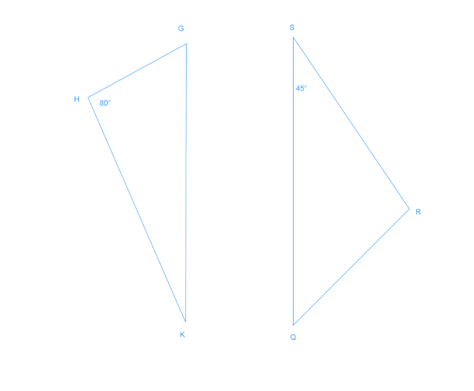
Congruence is a fundamental concept in geometry, particularly when studying triangles. Congruent triangles are identical in shape and size, with corresponding angles and sides equal. Our introduction video provides a visual explanation of this concept, serving as a crucial foundation for understanding congruence. This lesson will delve into various methods to prove triangle congruence, including Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA). These proofs are essential tools in geometry, allowing us to establish relationships between different triangles and solve complex problems. By mastering congruence, students can tackle more advanced geometric concepts and apply their knowledge to real-world situations, such as architecture and engineering. Throughout this lesson, we'll explore practical applications of congruent triangles, demonstrating how this seemingly abstract concept plays a vital role in our everyday lives and various professional fields.

Understanding the concept of corresponding angles and sides is crucial for solving problems related to congruent triangles. These problems often require students to identify and compare different parts of triangles to determine congruence. By practicing these skills, students can develop a deeper understanding of geometric principles and improve their problem-solving abilities. Additionally, the knowledge of congruent triangles and their properties can be applied to various real-world scenarios, making it a valuable topic in both academic and professional contexts.

Example

Which pairs of triangles are congruent?
Congruence and congruent triangles

Step 1: Understanding Congruent Triangles

To determine if two triangles are congruent, we need to understand the concept of congruence in geometry. Congruent triangles are triangles that are identical in shape and size. This means that all corresponding angles and sides of the triangles are equal. In other words, if triangle ABC is congruent to triangle DEF, then the following conditions must be met:

  • Angle A = Angle D
  • Angle B = Angle E
  • Angle C = Angle F
  • Side AB = Side DE
  • Side BC = Side EF
  • Side CA = Side FD

Step 2: Identifying Given Information

In the given problem, we are provided with two triangles, and we need to determine if they are congruent. The first step is to identify the information given in the diagram. Look for any marked angles or sides that indicate equality. For instance, if angle C is marked as equal to angle F, this is a piece of information we can use. Similarly, if any sides are marked as equal, note these as well.

Step 3: Analyzing Corresponding Angles and Sides

Next, we need to analyze the corresponding angles and sides of the two triangles. According to the given information:

  • Angle C is equal to angle F.
However, this is the only piece of information provided. There is no indication that angle B is equal to angle E or that any of the sides are equal. Without this additional information, we cannot conclusively determine that the triangles are congruent.

Step 4: Checking for Sufficient Information

To prove that two triangles are congruent, we need sufficient information. This can be achieved through various congruence criteria such as:

  • Side-Side-Side (SSS) Congruence: All three sides of one triangle are equal to all three sides of another triangle.
  • Side-Angle-Side (SAS) Congruence: Two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle.
  • Angle-Side-Angle (ASA) Congruence: Two angles and the included side of one triangle are equal to two angles and the included side of another triangle.
  • Angle-Angle-Side (AAS) Congruence: Two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle.
In this problem, we do not have enough information to apply any of these criteria.

Step 5: Conclusion

Based on the given information, we can conclude that there is not enough evidence to determine that the two triangles are congruent. We only know that one pair of angles is equal, which is insufficient to prove congruence. For triangles to be congruent, we need to verify that all corresponding angles and sides are equal, which is not possible with the limited information provided.

FAQs

Here are some frequently asked questions about congruence and congruent triangles:

  1. What is the difference between SSS and SAS congruence?

    SSS (Side-Side-Side) congruence requires all three sides of two triangles to be equal, while SAS (Side-Angle-Side) congruence requires two sides and the included angle to be equal. SSS is used when you have information about all sides, whereas SAS is used when you have information about two sides and the angle between them.

  2. Why is ASA congruence valid but AAA is not?

    ASA (Angle-Side-Angle) congruence is valid because it provides enough information to uniquely determine a triangle's shape and size. The side length fixes the scale, while the two angles determine the shape. AAA (Angle-Angle-Angle) only determines the shape but not the size, so it can only prove similarity, not congruence.

  3. Can SSA (Side-Side-Angle) be used to prove triangle congruence?

    SSA is not generally valid for proving triangle congruence due to the ambiguous case. It can result in two possible triangles, making it unreliable. However, there's an exception: the Hypotenuse-Leg (HL) theorem for right triangles, where SSA can be used if the given angle is the right angle.

  4. How does understanding triangle congruence help in real-world applications?

    Triangle congruence is crucial in various fields such as engineering, architecture, and surveying. It allows for accurate measurements, structural design, and problem-solving in situations where direct measurements are not possible. For example, in bridge construction, ensuring congruent support structures is essential for stability and load distribution.

  5. What is the CPCTC principle, and how does it relate to triangle congruence?

    CPCTC stands for "Corresponding Parts of Congruent Triangles are Congruent." This principle states that if two triangles are proven congruent, then all their corresponding parts (sides and angles) are also congruent. It's a powerful tool in geometry proofs, allowing us to deduce additional information about triangles once congruence is established.

Prerequisites

Understanding congruence and congruent triangles is a fundamental concept in geometry, but to fully grasp this topic, it's crucial to have a solid foundation in several prerequisite areas. These building blocks not only enhance your comprehension but also provide the necessary tools to solve more complex problems involving congruent triangles.

One essential prerequisite is the hypotenuse-leg theorem for right triangles. This theorem, which is closely related to the sine ratio, helps in understanding the relationships between sides and angles in right triangles. Mastering this concept is crucial because congruent triangles often involve comparing corresponding sides and angles, and the ability to calculate these elements accurately is paramount.

Another important foundation is understanding distance and time questions in linear equations. While this may seem unrelated at first glance, it actually plays a significant role in developing problem-solving skills and logical thinking, which are essential when proving triangle congruence. The ability to manipulate equations and understand relationships between variables directly translates to working with triangle properties and congruence proofs.

The concept of using sine ratios to calculate angles and sides is another critical prerequisite. This trigonometric principle is fundamental in analyzing triangles, especially when dealing with right triangles. Understanding sine ratios provides a powerful tool for comparing triangle properties, which is at the heart of proving congruence.

Lastly, familiarity with proving triangles congruent by ASA and AAS is a direct precursor to more advanced congruence concepts. These proofs introduce the logical steps and reasoning required to establish congruence between triangles. Mastering ASA (Angle-Side-Angle) and AAS (Angle-Angle-Side) proofs builds a strong foundation for understanding more complex congruence scenarios.

By solidifying your understanding of these prerequisite topics, you'll be well-equipped to tackle the intricacies of congruence and congruent triangles. Each of these concepts contributes to a comprehensive understanding of triangle properties, measurement, and proof techniques. As you progress in your study of geometry, you'll find that these foundational skills continually resurface, reinforcing their importance in mastering more advanced geometric concepts.

Remember, mathematics is a subject built on interconnected ideas. Taking the time to thoroughly understand these prerequisites will not only make learning about congruence and congruent triangles easier but will also enhance your overall mathematical prowess. As you delve into the world of congruent triangles, you'll appreciate how these foundational concepts come together to form a cohesive and powerful set of geometric tools.