Sign In
Sign Up
flag-us

Mastering Triangle Classification: Your Key to Geometry Success
Unlock the world of geometry by mastering triangle classification. Learn to identify and understand various triangle types, their properties, and real-world applications. Boost your problem-solving skills today!

  1. Intros0/1 watched
  2. Examples0/11 watched
  1. 0/1
  2. 0/11
Now Playing:Classifying triangles – Example 0a
Intros
0/1 watched
  1. Naming types of triangles based on their properties
    1. By angles
      • Acute
      • Right
      • Obtuse
    2. By sides
      • Scalene
      • Isosceles
      • Equilateral
Examples
0/11 watched
  1. Classify the triangle by its sides and angles.

    1. Classifying triangles: right triangle


    2. Classifying triangles: equilateral triangle


    3. Classifying triangles: isosceles triangle


    4. Classifying triangles: scalene triangle

Pythagorean theorem
Jump to:NotesConceptFAQsPrerequisites
Notes
Concept

Introduction to Classifying Triangles

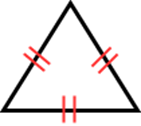
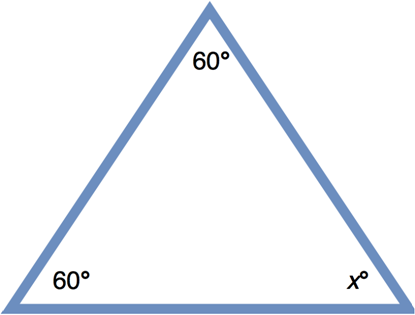
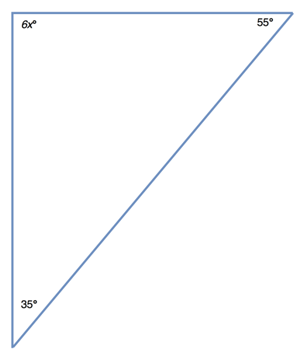
Welcome to the fascinating world of classifying triangles! Before we dive in, let's start with our introduction video, which provides an essential foundation for understanding this topic. This video will help you grasp the key concepts we'll be exploring. Now, let's talk about triangles. These three-sided shapes can be classified in two main ways: by their angles and by their sides. Each classification method reveals unique properties of the triangle. When we look at angles, we can identify right triangles, acute, and obtuse triangles. On the other hand, examining sides allows us to categorize triangles as equilateral, isosceles triangles, or scalene. Understanding these classifications is crucial in geometry and has practical applications in various fields. As we progress, you'll discover how these classifications help us solve problems and understand more complex geometric concepts. So, let's embark on this journey of triangle classification together!

When we delve deeper into the properties of triangles, we find that right triangles have a unique set of characteristics that make them particularly interesting. Similarly, isosceles triangles have two sides of equal length, which leads to some fascinating geometric properties. Additionally, understanding the different triangle sides helps in solving various mathematical problems. By mastering these concepts, you'll be well-equipped to tackle more advanced topics in geometry.

FAQs

  1. What are the three main types of triangles based on side lengths?

    The three main types of triangles based on side lengths are:

    • Equilateral: All three sides are equal in length
    • Isosceles: Two sides are equal in length
    • Scalene: All three sides have different lengths

  2. How are triangles classified based on their angles?

    Triangles are classified into three types based on their angles:

    • Acute: All angles are less than 90 degrees
    • Right: One angle is exactly 90 degrees
    • Obtuse: One angle is greater than 90 degrees

  3. What is special about a right triangle?

    A right triangle has one angle that measures exactly 90 degrees. It's significant in mathematics and real-world applications because:

    • It forms the basis for trigonometry
    • The Pythagorean theorem applies specifically to right triangles
    • It's commonly used in construction and engineering

  4. Can a triangle be classified by both its angles and sides simultaneously?

    Yes, a triangle can be classified by both its angles and sides at the same time. For example:

    • A right isosceles triangle has one 90-degree angle and two equal sides
    • An acute scalene triangle has all angles less than 90 degrees and all sides of different lengths
    • An equilateral triangle is also always acute, with all angles measuring 60 degrees

  5. What are some real-world applications of triangle classification?

    Triangle classification has numerous practical applications:

    • Architecture: Triangular shapes are used for structural stability in buildings and bridges
    • Engineering: Triangulation is used in surveying and navigation systems
    • Design: Triangles are used in graphic design to guide the viewer's eye
    • Computer Graphics: 3D modeling uses triangular polygons to create complex shapes
    • Sports: Strategic formations in games like basketball often involve triangular arrangements
Prerequisites

Understanding the classification of triangles is a fundamental skill in geometry, but to truly master this concept, it's crucial to have a solid grasp of several prerequisite topics. These foundational concepts not only enhance your understanding of triangle classification but also provide a broader perspective on geometric principles.

One of the key prerequisites is the ability to use tangent ratio to calculate angles and sides. This skill is essential for determining angle measurements in triangles, which is a critical aspect of classification. Similarly, using sine ratio to calculate angles and sides is equally important, especially when dealing with properties of right triangles.

A thorough understanding of isosceles and equilateral triangles is crucial for classification. This knowledge helps in recognizing the unique properties of equilateral triangles and how they differ from other types. Additionally, familiarity with the law of sines and the law of cosines is vital for solving more complex triangle problems and understanding the relationships between sides and angles in various triangle types.

The Pythagorean theorem and its applications form another crucial prerequisite. This theorem is not only fundamental for right triangles but also plays a role in understanding the relationships between sides in other triangle types.

By mastering these prerequisite topics, students gain a comprehensive toolkit for classifying triangles. The tangent and sine ratios provide methods for calculating unknown angles and sides, which is often necessary when determining a triangle's classification. Understanding isosceles and equilateral triangles helps in recognizing specific triangle types based on their unique properties.

The laws of sines and cosines extend this understanding to more complex scenarios, allowing for the analysis of triangles that aren't right-angled. These laws are particularly useful when dealing with obtuse triangles or when limited information is available about a triangle's dimensions.

Lastly, the Pythagorean theorem serves as a cornerstone in triangle classification, especially for identifying right triangles and understanding the relationships between side lengths in various triangle types.

In conclusion, a solid grasp of these prerequisite topics provides a strong foundation for classifying triangles. It enables students to approach triangle classification with confidence, armed with a diverse set of tools and a deep understanding of the underlying principles. This comprehensive knowledge not only aids in accurate classification but also enhances overall problem-solving skills in geometry.