Chord properties

Chord properties

In a circle, when a line passes through the center of the circle and is perpendicular to a chord, the line will bisect the chord. In other words, the perpendicular bisector of a chord always passes through the center of the circle.
Basic concepts: Angles in a circle, Tangent properties, Circles and circumference ,
Related concepts: Arcs of a circle, Areas and sectors of circles, Circle chord, tangent, and inscribed angles proofs,

Lessons

  • 1.
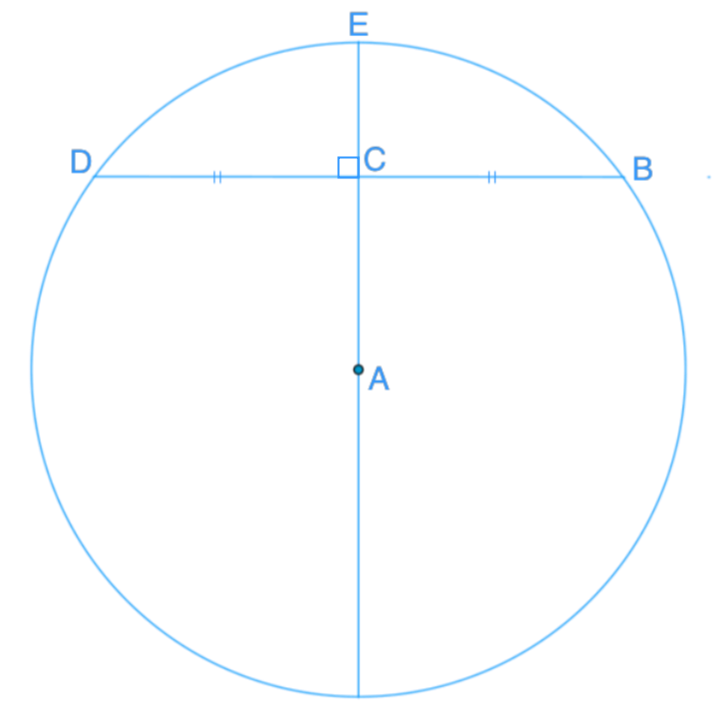
    If AC is 4 cm and BD is 15 cm, what is the diameter of the circle?
    using chord properties to determine diameter
  • 2.
    Zoe wants to set up her round dining table by putting a candle in the centre of it. How can she do that by using a tangent? Explain your answer with a diagram.
  • 3.
    Below is a segment of a circle, and A is the center of the circle. The radius is 15 cm, BC is 7.5 cm, and DE is 24 cm.
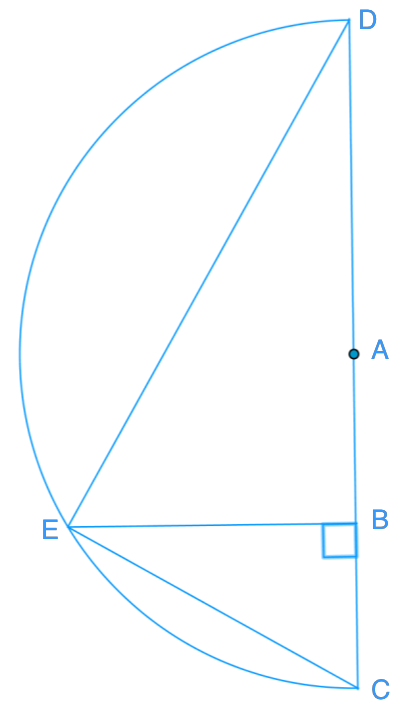
    Using chord properties to find radius and other unknowns
    Determine.
    a)
    ∠\angleCED

    b)
    CE

    c)
    BE

Do better in math today
Get Started Now
4.
Circles, plane and coordinate
4.1
Circles and circumference
4.2
Arcs of a circle
4.3
Areas and sectors of circles
4.4
Angles in a circle
4.5
Chord properties in circle geometry
4.6
Tangent properties in circle geometry
4.7
Central angles and proofs
4.8
Inscribed angles and proofs
4.9
Central and inscribed angles in circles
4.10
Circle chord, tangent, and inscribed angles proofs
Geometry
Don't just watch, practice makes perfect.