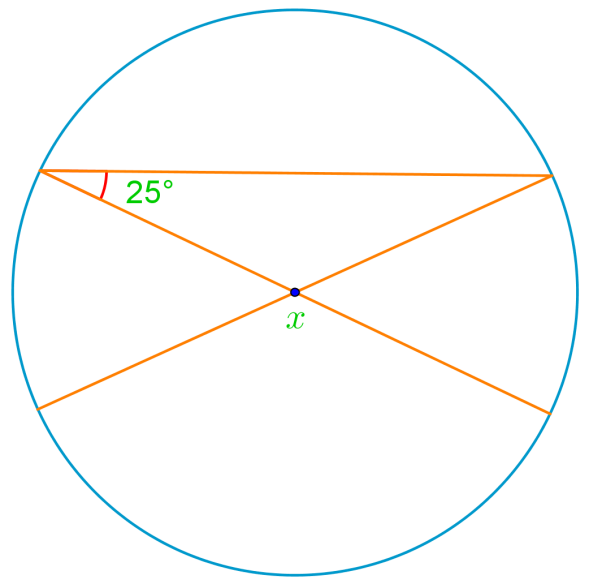
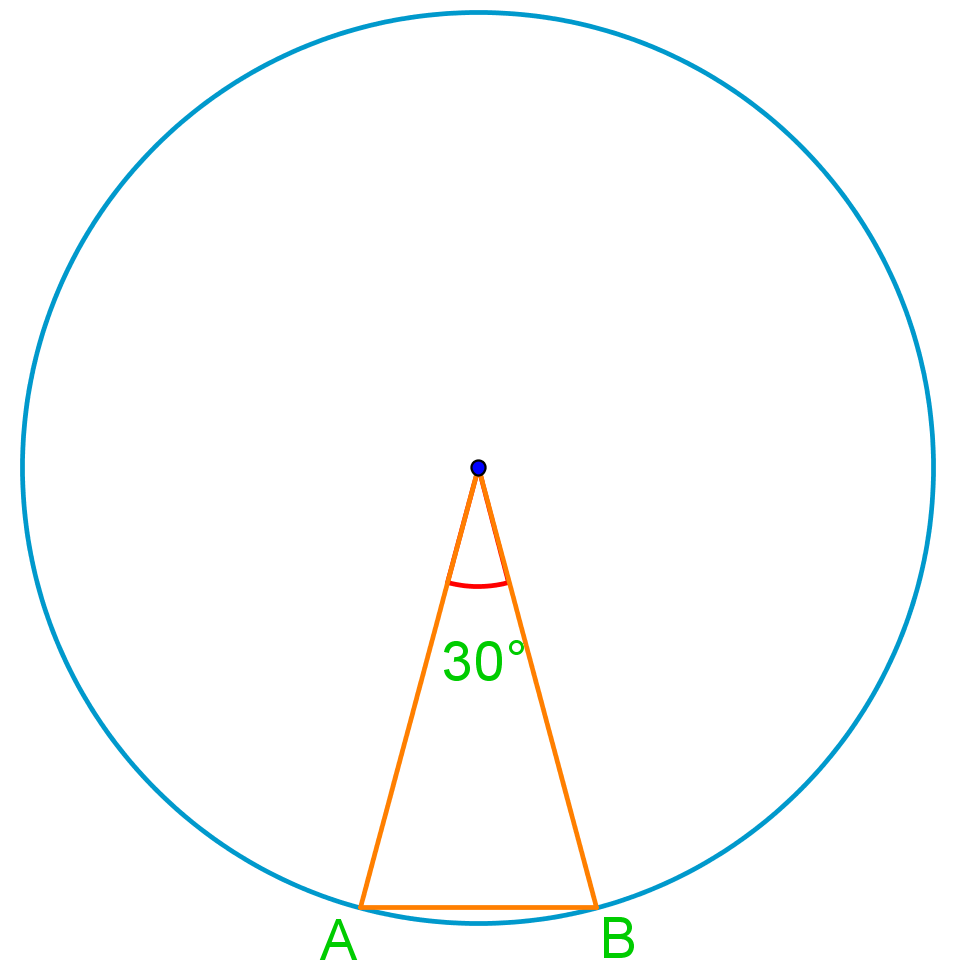
Central Angles and Proofs: Unlocking Circle Geometry

Dive into the world of central angles and circle proofs. Discover how these fundamental concepts form the backbone of geometry, from basic principles to real-world applications in architecture and engineering.

Find x

Step 1: Understand the Given Information

In this problem, we are given a circle with a central angle and a diameter. The central angle is marked as 40 degrees. The diameter of the circle is a straight line that passes through the center of the circle, dividing it into two equal halves. This information is crucial for solving the problem.

Step 2: Recognize the Properties of a Diameter

The diameter of a circle is a straight line that passes through the center of the circle, creating a straight angle. A straight angle measures 180 degrees. This property is essential because it helps us understand that the total angle formed by the diameter is 180 degrees.

Step 3: Identify the Relationship Between the Given Angle and the Diameter

Since the diameter forms a straight angle of 180 degrees, and we are given a central angle of 40 degrees, we can use this information to find the unknown angle, x. The central angle and the unknown angle together form the straight angle of 180 degrees.

Step 4: Set Up the Equation

To find the unknown angle, x, we need to set up an equation that represents the relationship between the given angle and the total angle formed by the diameter. The equation is as follows:

180 degrees (total angle) = 40 degrees (given angle) + x (unknown angle)

Step 5: Solve for x

To solve for x, we need to isolate x on one side of the equation. We can do this by subtracting the given angle from the total angle:

x = 180 degrees - 40 degrees

By performing the subtraction, we find that:

x = 140 degrees

Step 6: Verify the Solution

To ensure that our solution is correct, we can verify that the sum of the given angle and the unknown angle equals the total angle formed by the diameter. In this case, 40 degrees (given angle) + 140 degrees (unknown angle) = 180 degrees (total angle). Since the sum is correct, our solution is verified.

Conclusion

By following these steps, we have successfully found the unknown angle, x, using the properties of the diameter and the given central angle. This method can be applied to similar problems involving central angles and diameters in circles.

1. What is the difference between a central angle and an inscribed angle?

   A central angle has its vertex at the center of the circle, while an inscribed angle has its vertex on the circle's circumference. The measure of a central angle is always twice that of an inscribed angle that subtends the same arc.

2. How do you calculate the measure of an inscribed angle?

   The measure of an inscribed angle is half the measure of the central angle that subtends the same arc. Alternatively, it's half the measure of the arc it intercepts on the circle.

3. What is the inscribed angle theorem?

   The inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc on a circle. This theorem is fundamental in solving many circle geometry problems.

4. Why is an angle inscribed in a semicircle always a right angle?

   An angle inscribed in a semicircle is always 90 degrees (a right angle) because it intercepts a diameter, which subtends a central angle of 180 degrees. Since an inscribed angle is half the measure of the central angle, it must be 90 degrees.

5. How are central and inscribed angles used in real-world applications?

   Central and inscribed angles have numerous practical applications, including architecture (designing circular structures), navigation (determining distances and positions), optics (lens design), and engineering (circular motion analysis). They're also used in surveying, astronomy, and many other fields requiring precise angular measurements.

Understanding central angles and proofs is a crucial aspect of geometry and trigonometry. To fully grasp this concept, it's essential to have a solid foundation in several prerequisite topics. One of the most fundamental prerequisites is radian measure and arc length, which provides the basis for measuring angles in a circular context.

Another important concept to master is angles in a circle. This topic helps students understand how angles are formed within circular shapes and how they relate to central angles. Additionally, knowledge of tangent properties is crucial, as it allows for a deeper understanding of how lines interact with circles, which is often a key component in central angle proofs.

When dealing with more advanced problems involving central angles, students may need to apply arc length calculation techniques. This skill is particularly useful when working with complex geometric figures or in calculus-related problems. Understanding the relationship between central angles and chords is also vital, as it forms the basis for many theorems and proofs in this area.

For students tackling problems involving right angles, knowing how to use tangent ratios to calculate angles and sides can be incredibly helpful, especially when dealing with right angles in semicircles. This knowledge ties directly into the broader concept of central angles and their properties.

While not directly related, understanding the central limit theorem can provide valuable insights into the concept of centrality in mathematics, which can be beneficial when studying central angles. Lastly, familiarity with the angle of elevation and depression can enhance a student's spatial reasoning skills, which are crucial when visualizing and solving problems related to central angles and their proofs.

By mastering these prerequisite topics, students will be well-equipped to tackle the challenges presented by central angles and proofs. Each of these concepts builds upon the others, creating a comprehensive understanding of circular geometry and its applications. As students progress through these topics, they'll find that their ability to solve complex problems and construct rigorous proofs improves significantly, setting a strong foundation for advanced mathematical studies.