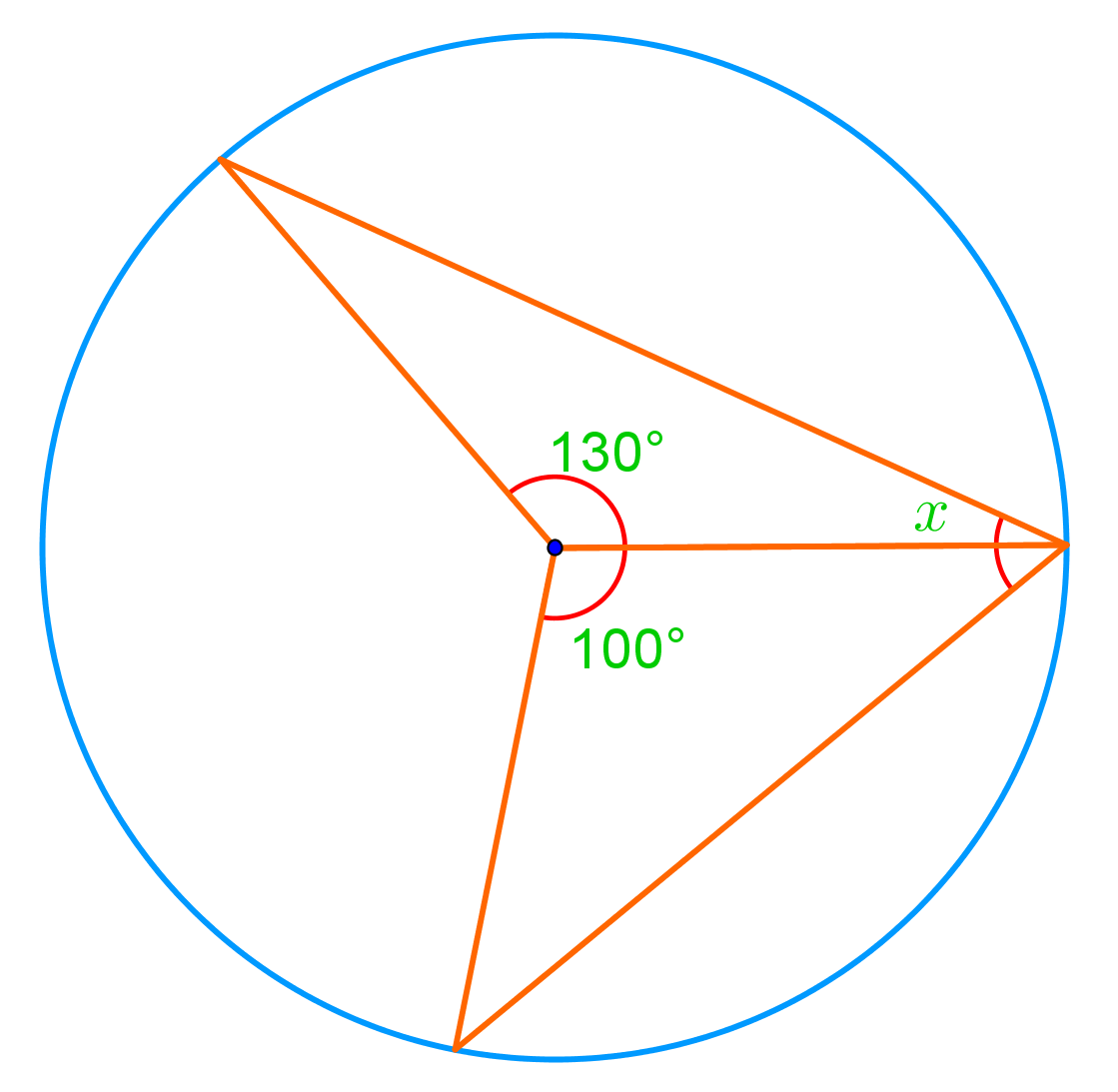
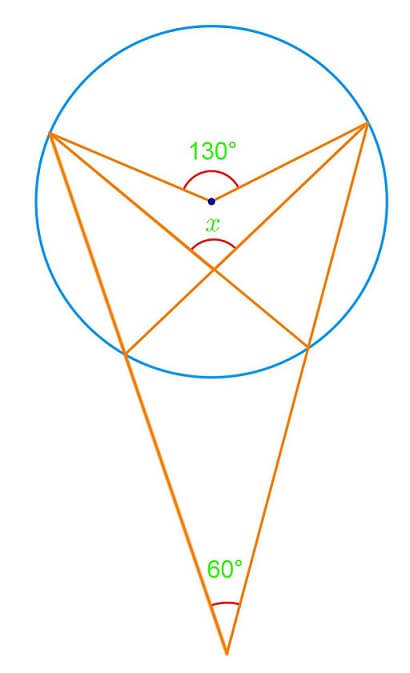
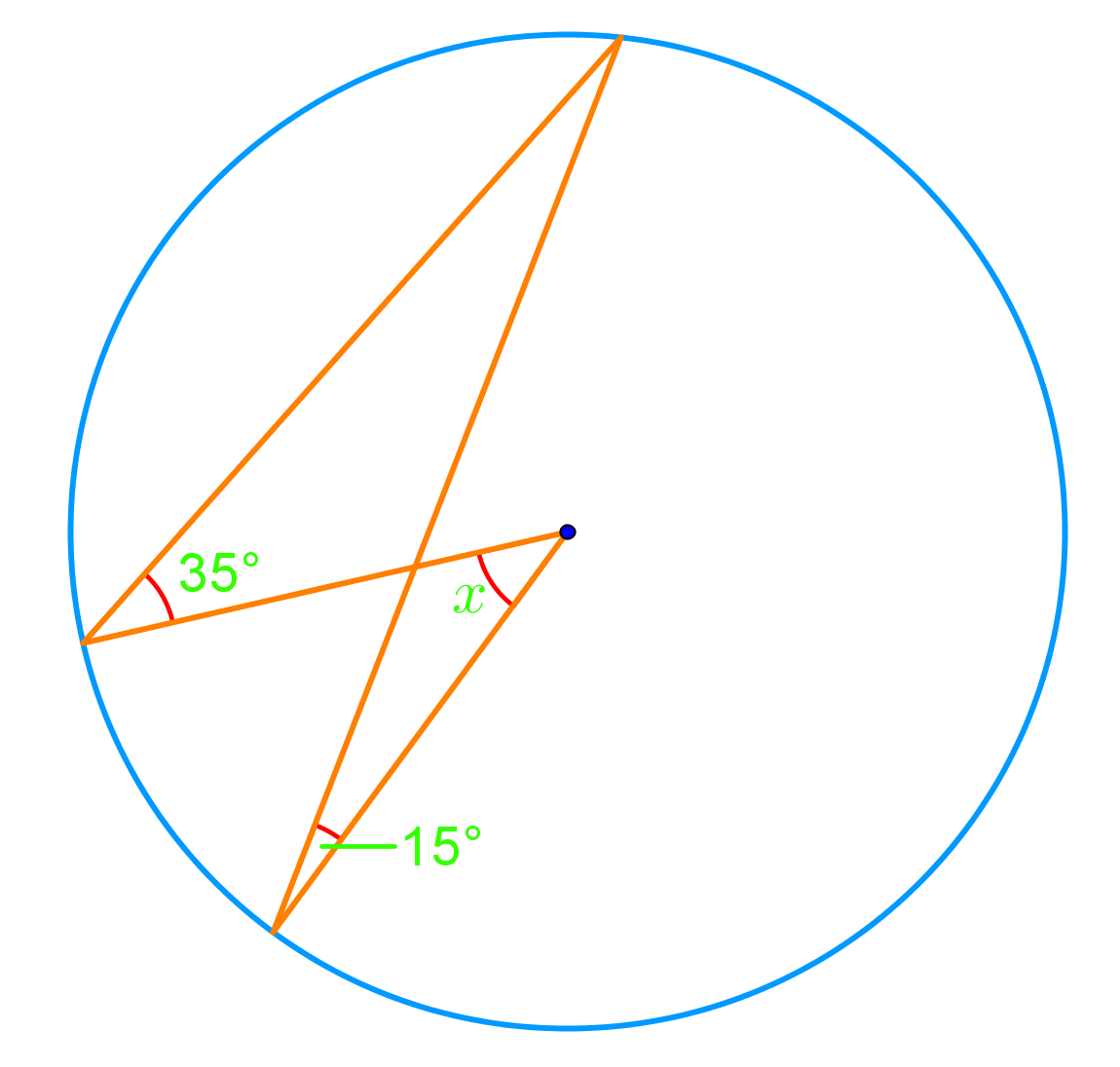
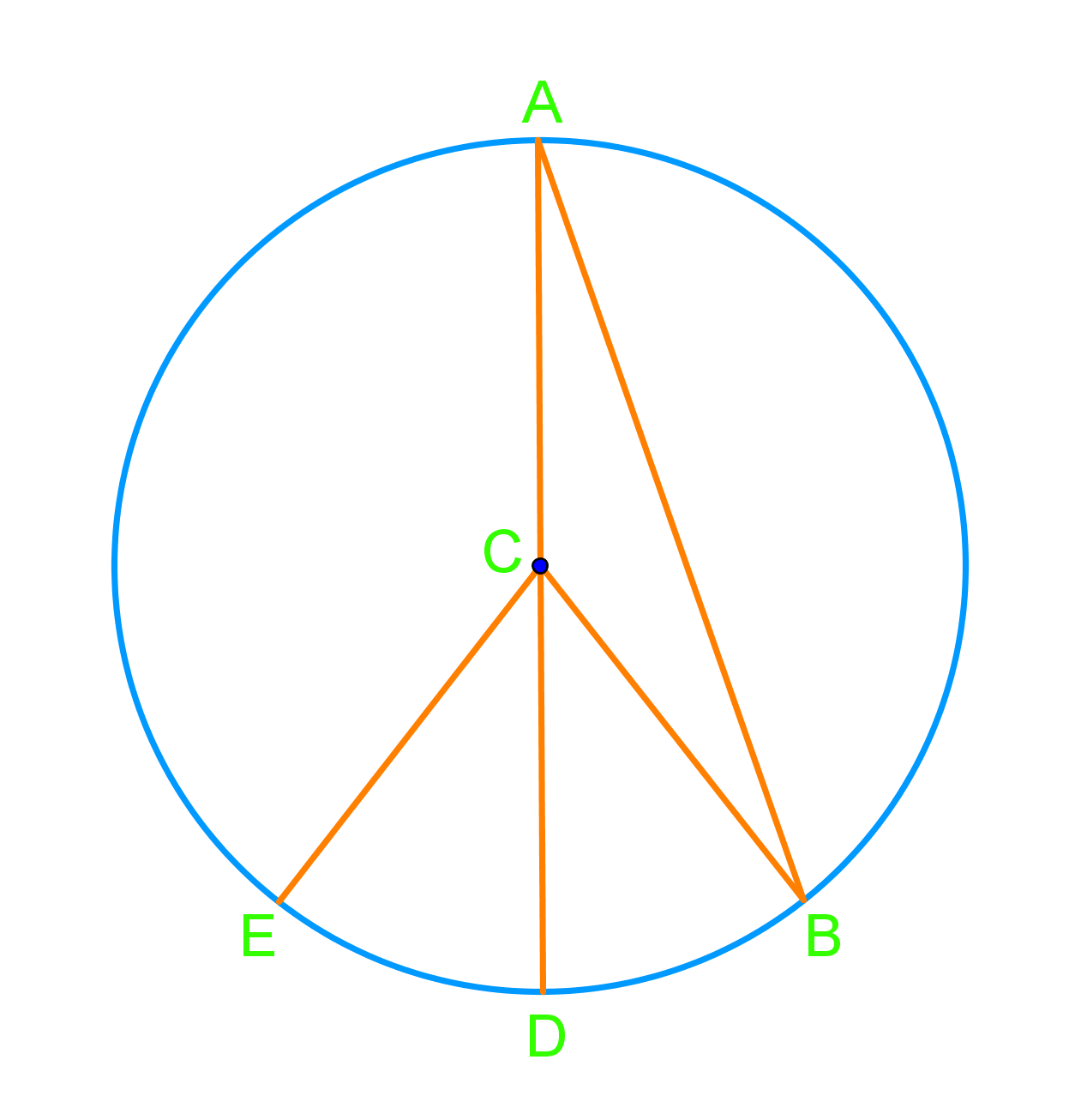
Introduction
Circle geometry and inscribed angles are fundamental concepts in circle geometry, playing a crucial role in understanding the relationships between angles and arcs within circles. Our introduction video provides a comprehensive overview of these essential topics, serving as a valuable starting point for students and enthusiasts alike. This article delves into the key concepts, properties of inscribed angles, and relationships between angles and arcs, offering a deeper understanding of their significance in circular geometry. We'll explore how central angles, which have their vertex at the circle's center, differ from inscribed angles, which have their vertex on the circle's circumference. By examining these angles and their properties of inscribed angles, we'll uncover important theorems and practical applications in mathematics and real-world scenarios. Whether you're a student preparing for exams or simply curious about circle geometry, this exploration of central and inscribed angles will enhance your understanding of these fascinating mathematical concepts.