Similar solids

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

?
Intros
Lessons
  1. Introduction to Similar Solids
  2. When are two objects similar?
  3. Scale factor vs. surface area ratio vs. volume ratio
?
Examples
Lessons
  1. Identify Similar Solids

    Which of the following are similar solids?

    1. MATH7 19 1 1a1 MATH7 19 1 1a2
    2. MATH7 19 1 1b1 MATH7 19 1 1b2
  2. Proof of the Relationships Between Scale Factor, Area Ratio and Volume Ratio

    Use the following similar solids to prove the relationships between the scale factor, surface area ratio and volume ratio.

    MATH7 19 1 2 1 MATH7 19 1 2 2
    1. Given the Scale Factors, Find a Surface Area

      Given two similar hemispheres. The radius of the smaller hemisphere is 5m5m and that of the larger hemisphere is 7m7m. If the surface area of the larger hemisphere is 147m2147m^{2}, what is the surface area of the smaller hemisphere?

      1. Given the Volumes, Find the Scale Factors

        Given that the volumes of the two similar prisms are 729cm3729cm^{3} and 1331cm31331cm^{3} respectively. What is the scale factor of the smaller prism to the larger prism?

        1. Scale Factors Doubled, Find a Volume

          The dimensions of a pyramid figure with a volume of 24m324m^{3} have been doubled. What is the volume of the new pyramid figure?

          Topic Notes
          ?

          In this lesson, we will learn:

          • Identify Similar Solids
          • Proof of the Relationships Between Scale Factor, Area Ratio and Volume Ratio
          • Given the Scale Factors, Find a Surface Area
          • Given the Volumes, Find the Scale Factors
          • Scale Factors Doubled, Find a Volume

          • Solid: A three-dimensional object
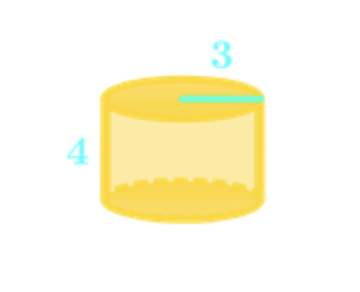
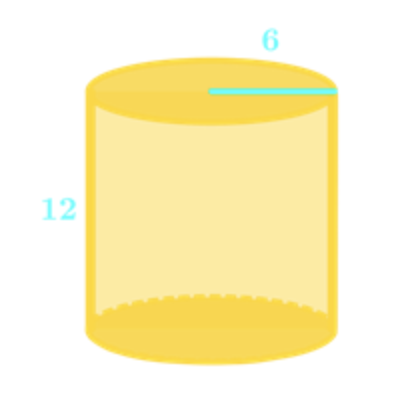
          • Two solids are similar when the ratios of their corresponding measures are constant.
          • Scale factor:
            • The ratios of the corresponding measures of two objects.
            • A numeric multiplier used for scaling.
          • If two similar solids have a scale factor of ab\frac{a}{b}, then
            1. They have a surface area ratio of (ab)2(\frac{a}{b})^{2}.
            2. They have a volume ratio of (ab)3(\frac{a}{b})^{3}.