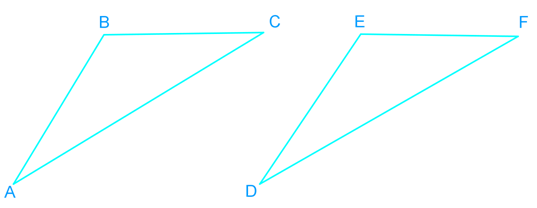
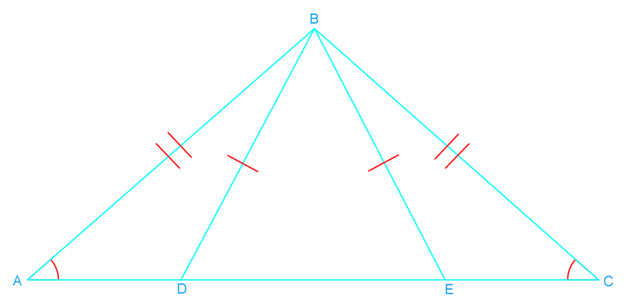
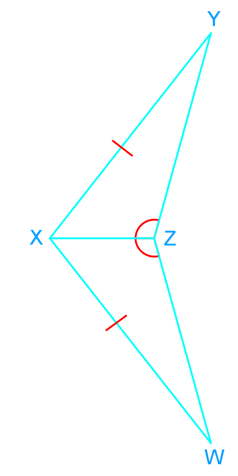
Mastering Triangle Congruence: ASA and AAS Proofs

Unlock the power of geometric reasoning with our in-depth guide to ASA and AAS proofs. Learn to confidently prove triangle congruence and apply these skills to advanced geometry problems.

What is the third congruence that is needed to prove that $\triangle ABC$$\cong$$\triangle DEF$ using the given postulate or theorem?

$\overline {AB}$$\cong$$\overline {DE}$ and $\angle C$$\cong$$\angle F$
Prove by AAS.

Step 1: Identify Given Information

First, identify the given information in the problem. We are provided with two pieces of information:

• $\overline {AB}$$\cong$$\overline {DE}$: This means that side AB of $\triangle ABC$ is congruent to side DE of $\triangle DEF$.
• $\angle C$$\cong$$\angle F$: This means that angle C of $\triangle ABC$ is congruent to angle F of $\triangle DEF$.

Step 2: Understand the AAS Postulate

The Angle-Angle-Side (AAS) postulate states that if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent. In this case, we need to find another angle in $\triangle ABC$ that is congruent to the corresponding angle in $\triangle DEF$.

Step 3: Determine the Third Congruence

To use the AAS postulate, we need to identify a third congruence. This can be either:

• $\angle A$$\cong$$\angle D$: If angle A in $\triangle ABC$ is congruent to angle D in $\triangle DEF$, then we have two angles and a non-included side congruent.
• $\angle B$$\cong$$\angle E$: Alternatively, if angle B in $\triangle ABC$ is congruent to angle E in $\triangle DEF$, we also have two angles and a non-included side congruent.

Step 4: Verify the Non-Included Side

Ensure that the side $\overline {AB}$ (or $\overline {DE}$) is not included between the two angles we are using. This is crucial for the AAS postulate. In this case, $\overline {AB}$ is not between $\angle C$ and either $\angle A$ or $\angle B$, and similarly, $\overline {DE}$ is not between $\angle F$ and either $\angle D$ or $\angle E$.

Step 5: Conclude the Congruence

Once we have identified the third congruence, we can conclude that $\triangle ABC$$\cong$$\triangle DEF$ by the AAS postulate. This means that all corresponding sides and angles of the two triangles are congruent.

Here are some frequently asked questions about ASA and AAS proofs:

1. What are the 5 ways to prove triangles are congruent?

The five ways to prove triangles congruent are: SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and HL (Hypotenuse-Leg for right triangles).

2. How do you prove that a pair of triangles are congruent?

To prove triangles congruent, you need to show that three corresponding parts of the triangles are equal. This can be done using one of the congruence theorems (SSS, SAS, ASA, AAS, or HL) depending on the given information.

3. What is the ASA postulate proof?

The ASA (Angle-Side-Angle) postulate states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent. This is proven using the fact that the third angle is determined by the other two, and the remaining sides are fixed by the given side and angles.

4. What does AAS prove?

AAS (Angle-Angle-Side) proves that two triangles are congruent if two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle. This works because the third angle is determined by the other two, making it equivalent to ASA.

5. How do you tell SSS, SAS, ASA, and AAS apart?

To distinguish between these proofs, look at the given information: - SSS: All three sides are congruent - SAS: Two sides and the included angle are congruent - ASA: Two angles and the included side are congruent - AAS: Two angles and a non-included side are congruent Pay attention to the order and relationship between the given parts to determine which proof to use.

Understanding triangles congruent by ASA (Angle-Side-Angle) and AAS (Angle-Angle-Side) proofs is a crucial concept in geometry. However, to fully grasp these proofs, it's essential to have a solid foundation in several prerequisite topics. Let's explore how these fundamental concepts contribute to your understanding of ASA and AAS proofs.

First and foremost, a strong grasp of congruent triangles is vital. This concept forms the basis for ASA and AAS proofs, as these methods are used to prove that two triangles are indeed congruent. Understanding the criteria for congruence will help you recognize when and how to apply ASA and AAS proofs effectively.

Knowledge of angle bisectors is also crucial. In ASA and AAS proofs, you'll often need to identify and work with angles, including those created by angle bisectors. This understanding helps in recognizing the relationships between angles in different triangles, which is key to proving congruence.

The concept of parallel lines and corresponding angles plays a significant role in these proofs. Often, ASA and AAS situations arise in configurations involving parallel lines, where corresponding angles are congruent. This knowledge helps in identifying congruent angles across different triangles.

Similarly, understanding perpendicular bisectors is beneficial. While not directly used in ASA or AAS proofs, this concept enhances your overall geometric intuition, which is valuable when analyzing triangle congruence.

A solid understanding of the sum of angles in a triangle is essential. This fundamental property of triangles is often used in conjunction with ASA and AAS proofs to deduce the measures of unknown angles, which can be crucial in establishing congruence.

Lastly, familiarity with right angles in triangles is important. While ASA and AAS proofs apply to all types of triangles, understanding right triangles provides a strong foundation for triangle congruence concepts in general.

By mastering these prerequisite topics, you'll be well-equipped to tackle ASA and AAS proofs with confidence. Each concept builds upon the others, creating a comprehensive understanding of triangle congruence. Remember, geometry is all about relationships and patterns the more connections you can make between these topics, the stronger your grasp of ASA and AAS proofs will be.