Parallel Lines and Transversals: Understanding Angle Relationships

Master the concepts of parallel lines cut by transversals. Learn to identify and apply angle relationships, solve complex problems, and enhance your geometric reasoning skills.

Parallel lines

What are parallel lines? They are lines that are equidistant (the same distance apart) from each other but never meet. They also point in the same direction.

When a set of parallel lines gets cut by another line, that other line is called a transversal. Having this transversal line paves the way for a variety of helpful information that we can derive from the parallel lines' angles.

What are corresponding angles

When we've got a line with a transversal through it, we can identify corresponding angles from the two parallel lines that are the same. Therefore, corresponding angles are equal. This is the corresponding angles definition. We'll have a chart below to summarize this and the following concept at the end with visual depictions of what these terms mean.

What are alternate interior angles

Alternate interior angles are found on the opposite sides of the transversal but inside the two lines. These angles are on the interior of the lines that cross, but on alternate sides of the transversal. This is the alternate interior angles definition.

Here's a summary chart of the above concepts, plus a few more pairs of angles that come about due to parallel lines and a transversal. Unlike regular pairs of lines and angles, these ones have special rules to their angles based off the parallel lines. They'll be very useful in helping you solve questions related to pairs of angles.

Example questions

Question 1:

Find the missing values and then explain your reasoning.

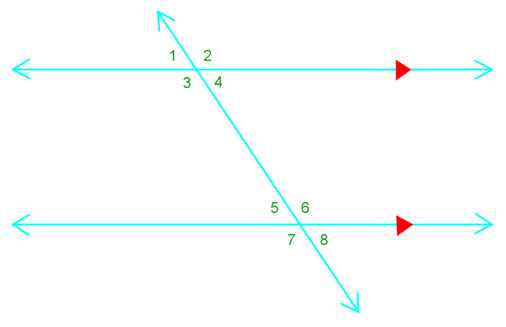
a) angle 6 $\cong$ ?

b) angle 2 $\cong$ ?

c) if m angle 8 = 60°, m angle 1 = ?

d) angle 3 and angle ? are supplementary

Solutions:

a) angle 6 $\cong$ ?

Angle 6 is congruent to angle 2 due to the corresponding angle rule.

Angle 6 is also congruent to angle 7 due to vertical angle congruence.

Lastly, angle 6 is congruent to angle 3 because of the corresponding angle rule between angle 3 and angle 7.

b) angle 2 $\cong$ ?

Angle 2 is equalled to angle 6 since they're corresponding angles.

Angle 2 is also congruent to angle 3 due to vertical angle congruence.

Lastly, angle 2 is congruent to angle 7 based on the corresponding angle rule or alternate exterior angle theorem.

c) if m angle 8 = 60°, m angle 1 = ?

We get that m angle 1 = 60°. This is based on the alternate exterior angle theorem.

d) angle 3 and angle ? are supplementary

Supplementary means that the sum the two angles = 180°

So angle 3 + angle 5 is supplementary due to the consecutive interior angle theorem.

In addition, angle 8, angle 1, angle 4 are also supplementary to angle 3.

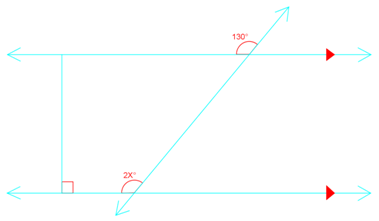
Question 2:

Find the value of x.

Solution:

Angle 130° = 2x°

So,

130 = 2x

65° = x

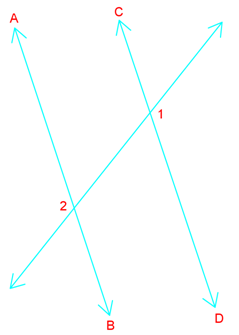
Question 3:

Write a two-column proof.

Given: AB||CD

Prove: angle 1 $\cong$ angle 2

Solution:

Take a look at this interactive online diagram to help you see the angle relationships that exist when there is a set of parallel lines and a transversal.

To move further into this concept, learn more about parallel line equation and how to deal with a combination of parallel and perpendicular line equations.

• Pairs of lines and angles

• Parallel line equation
• Combination of both parallel and perpendicular line equations