Introduction to transformations

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

Get the most by viewing this topic in your current grade. Pick your course now.

?
Intros
Lessons
  1. Types of transformations:
    What are translations, reflections and rotations?
?
Examples
Lessons
  1. Draw the reflection image of the following diagram. The line of reflection is labeled rr.
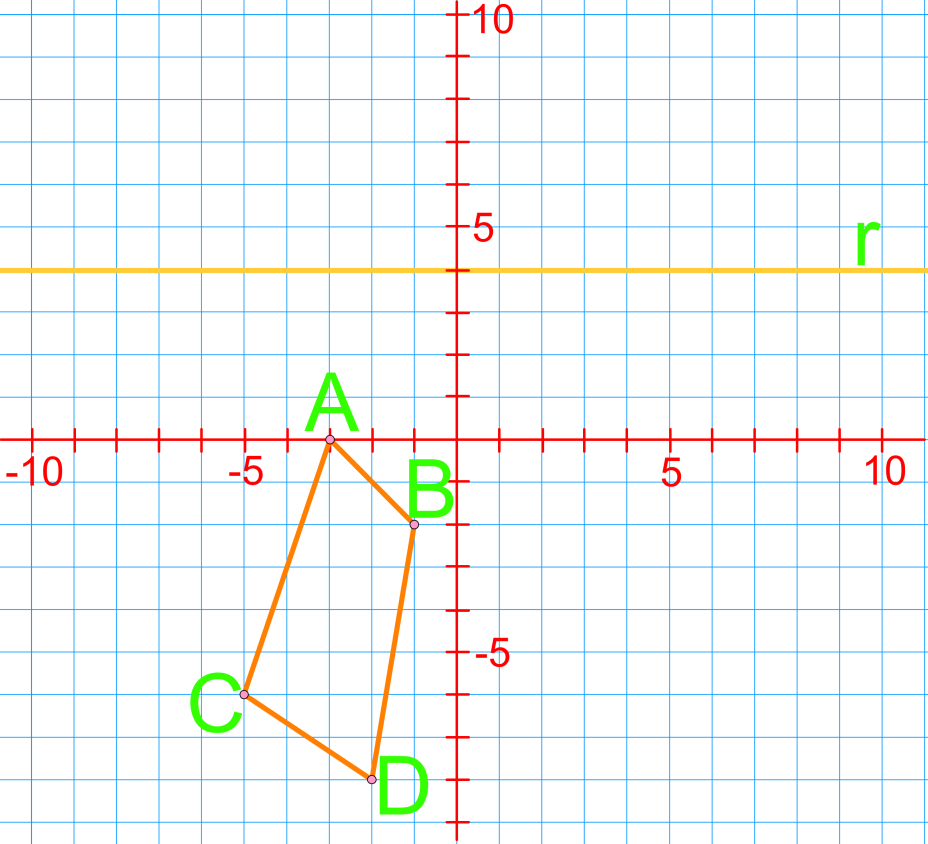
    Reflect the object
    1. The diagram shows a quadrilateral. Rotate the figure 180 degrees counter clockwise about its centre of rotation, P.
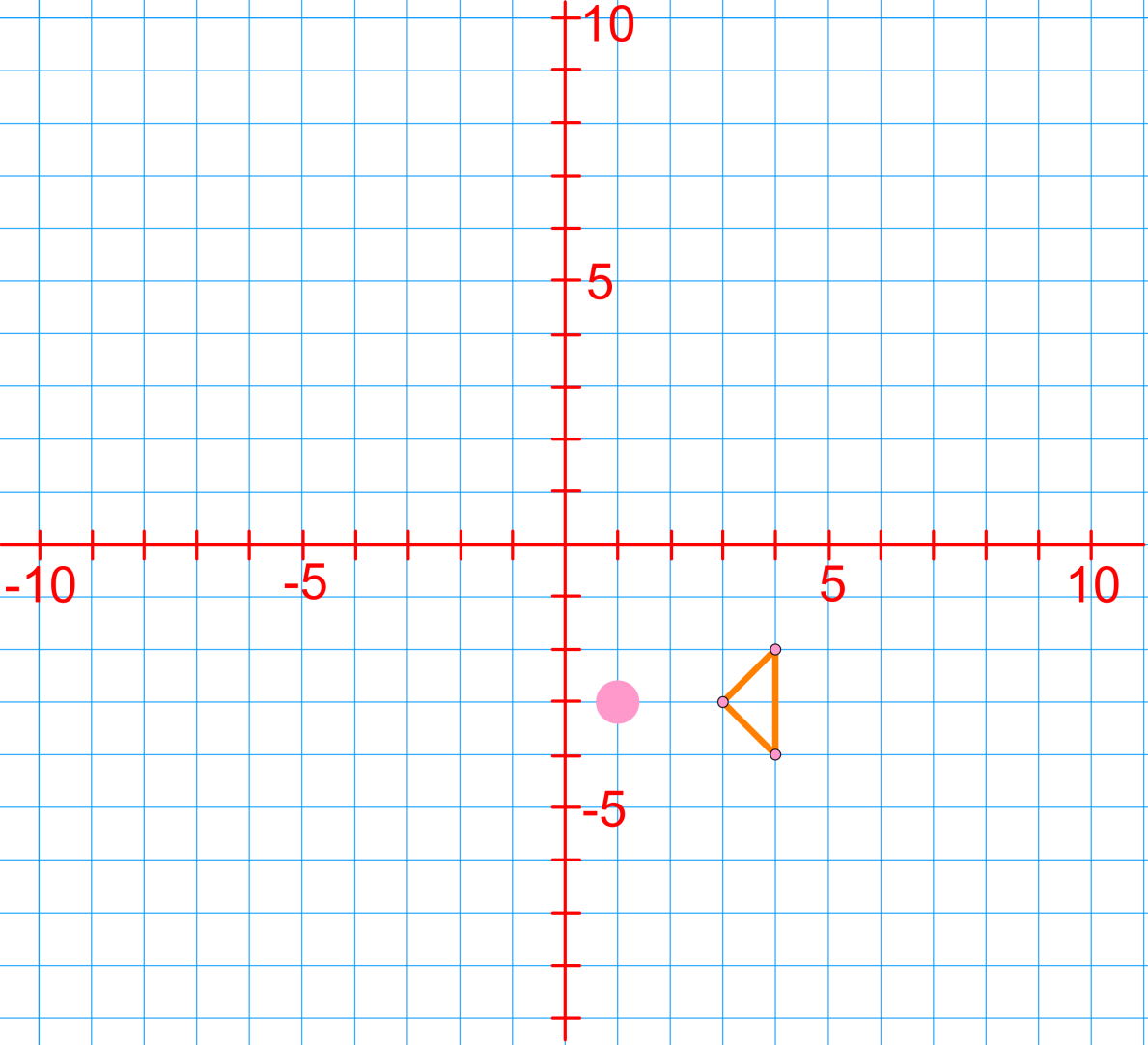
      Introduction to transformations, rotations of object
      Topic Notes
      ?
      When an object is reflected in a mirror, the line of reflection is the mirror. Reflections are a type of transformation. In this section, we will use our knowledge from sections on Cartesian plane and drawing on coordinate planes to show transformations of figures on coordinate planes. Along with reflections, translations and rotations are types of transformations. When showing translations, we always describe horizontal (left or right) movements before vertical (up or down) movements.
      Basic Concepts
      ?
      Related Concepts
      ?