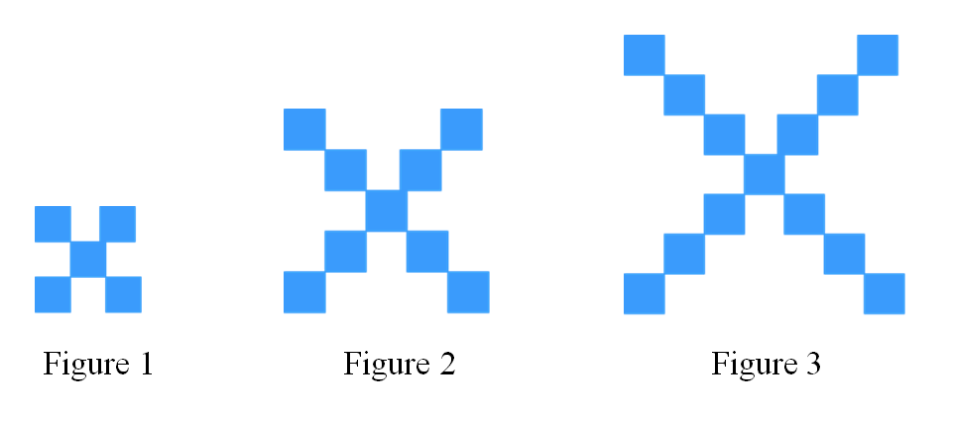
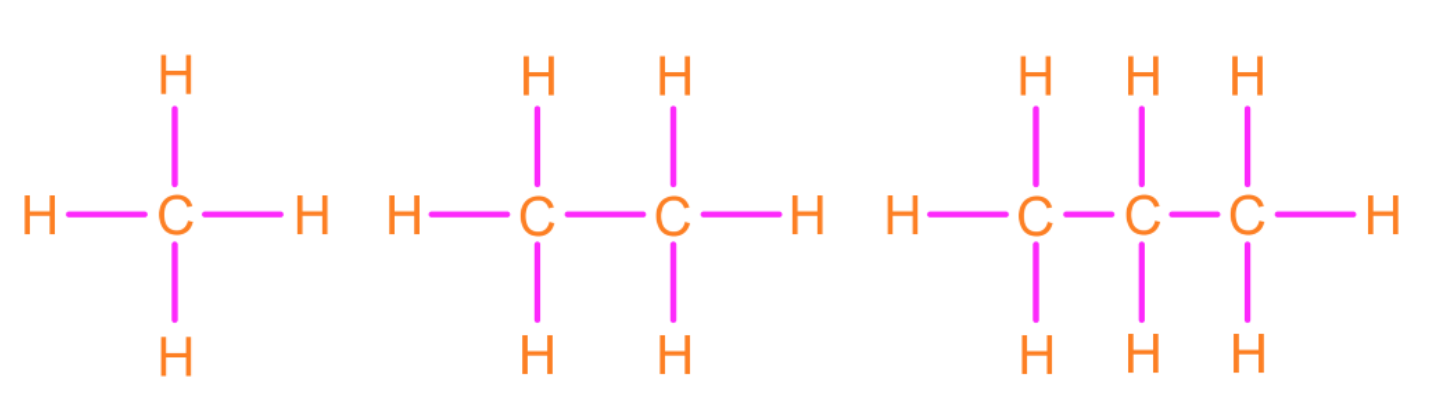
A conjecture is an educational guess made from the given information. Inductive reasoning is about making a conjecture that predicts the next set of patterns, or arrive at a conclusion.
Unlock the Power of Inductive Reasoning in Mathematics Explore inductive reasoning to boost your math skills. Learn to draw conclusions from observations, identify patterns, and make predictions. Perfect for beginners and those looking to enhance their problem-solving abilities.
- Making a Conjecture
Make a conjecture of the next item or number based on the information given:
- Make a conjecture with the given information. Draw a figure to show that your conjecture is correct:
- Counterexamples of Conjectures
Determine if the following conjecture is true or false. If it is false, then find a counterexample of the conjecture:
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
A conjecture is an educational guess made from the given information. Inductive reasoning is about making a conjecture that predicts the next set of patterns, or arrive at a conclusion.
Introduction to Inductive Reasoning
Inductive reasoning is a fundamental concept in mathematics that plays a crucial role in problem-solving and logical thinking. This powerful method allows us to draw general conclusions from specific observations, helping us identify patterns and make predictions. In mathematics, inductive reasoning is essential for developing conjectures, proving theorems, and understanding complex mathematical structures. Our introduction video on inductive reasoning will guide you through the basics of this important concept, providing clear examples and explanations to help you grasp its significance. You'll learn how to apply inductive reasoning to various mathematical problems and see how it connects to other areas of study. Whether you're a beginner or looking to refresh your knowledge, this video will equip you with the tools to enhance your mathematical reasoning skills. By understanding inductive reasoning, you'll be better prepared to tackle advanced mathematical concepts and develop a more intuitive approach to problem-solving.
-
What is inductive reasoning?
Inductive reasoning is a logical process where specific observations or examples are used to form general conclusions or principles. In mathematics, it involves recognizing patterns and making educated guesses (conjectures) based on available evidence. This method of thinking allows us to draw broader inferences from limited data, which can then be tested and verified.
-
How does inductive reasoning differ from deductive reasoning?
While inductive reasoning moves from specific observations to general conclusions, deductive reasoning works in the opposite direction. Deductive reasoning starts with general principles and applies them to specific cases. Inductive reasoning is more exploratory and can lead to new hypotheses, while deductive reasoning is used to prove or disprove statements based on established rules or axioms.
-
Can you give an example of inductive reasoning in mathematics?
A classic example is the sequence 2, 4, 6, 8. Using inductive reasoning, we might observe that each number increases by 2. We could then conjecture that the next number in the sequence would be 10, and the general rule for the nth term would be 2n. This conclusion is reached by observing a pattern in specific cases and generalizing it.
-
How are conjectures related to inductive reasoning?
Conjectures are educated guesses or propositions formed through inductive reasoning. They are based on observed patterns or limited evidence but haven't been proven definitively. In mathematics, conjectures often serve as starting points for further investigation and can lead to important theorems if proven true.
-
Why is it important to be able to disprove conjectures?
Disproving conjectures is crucial in mathematics for several reasons. It helps refine our understanding of concepts, challenges assumptions, and often leads to new insights. Finding counterexamples to disprove a conjecture can reveal limitations in our thinking and prompt us to develop more accurate theories. This process is essential for the advancement of mathematical knowledge and the development of critical thinking skills.
Understanding inductive reasoning is crucial in many fields of study, from mathematics to science and logic. To fully grasp this concept, it's essential to have a solid foundation in certain prerequisite topics. Two key areas that contribute significantly to understanding inductive reasoning are converting from general to vertex form by completing the square and applications of the Pythagorean theorem.
Inductive reasoning involves drawing general conclusions from specific observations. This process is similar to how we approach mathematical problems, particularly in algebra and geometry. When we look at converting from general to vertex form by completing the square, we're essentially moving from a broad, general equation to a more specific, focused form. This mirrors the inductive reasoning process, where we start with specific instances and work towards a general principle.
The skill of completing the square helps students understand how to manipulate equations and see patterns, which is crucial in inductive reasoning. By practicing this algebraic technique, students develop the ability to recognize relationships between variables and constants, a key component in forming general conclusions from specific cases.
Similarly, the applications of the Pythagorean theorem provide an excellent foundation for inductive reasoning. This fundamental geometric principle demonstrates how a specific relationship (between the sides of a right triangle) can be applied to various real-world situations. Understanding how to use the Pythagorean theorem in different contexts helps students see how a single principle can be generalized to solve diverse problems.
When students work with the Pythagorean theorem, they're essentially practicing inductive reasoning. They start with a specific rule about right triangles and then apply it to various scenarios, gradually building a broader understanding of its applications. This process of taking a specific concept and expanding its use to more general situations is at the heart of inductive reasoning.
Both of these prerequisite topics enhance a student's ability to recognize patterns and relationships, which is essential in inductive reasoning. By mastering these concepts, students develop the analytical skills needed to observe specific instances, identify common threads, and formulate general principles or hypotheses.
In conclusion, while inductive reasoning might seem abstract at first, its foundations are rooted in concrete mathematical concepts. By understanding and practicing topics like completing the square and applying the Pythagorean theorem, students build the necessary skills to excel in inductive reasoning. These prerequisites not only provide a solid mathematical foundation but also cultivate the critical thinking abilities crucial for success in higher-level reasoning and problem-solving across various disciplines.