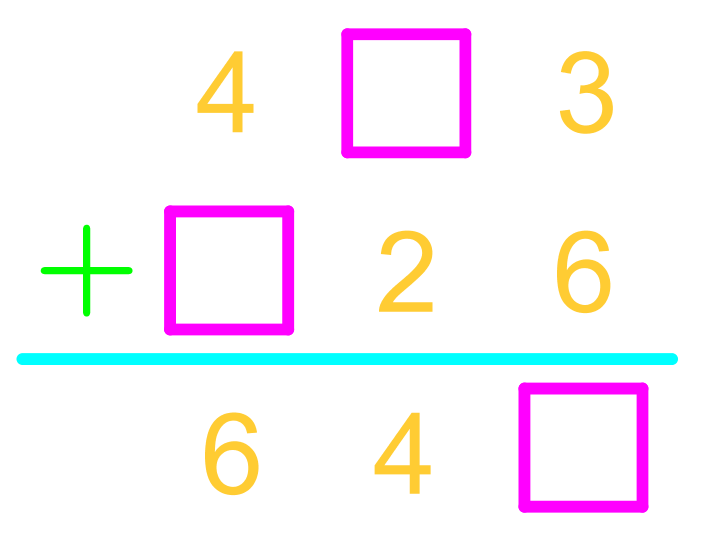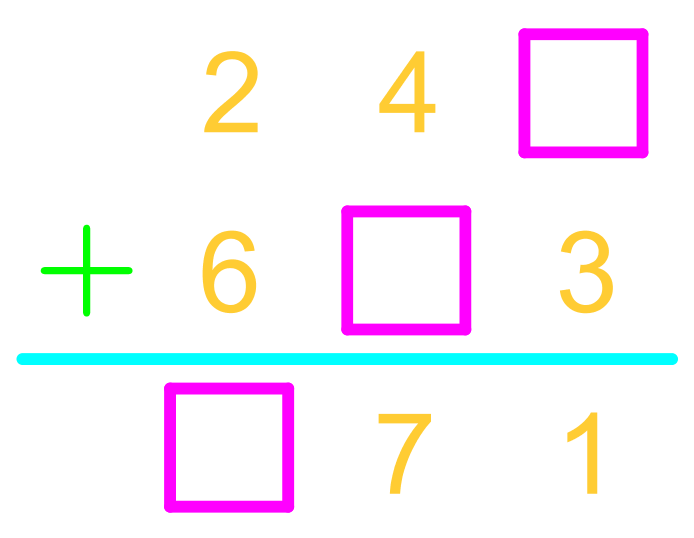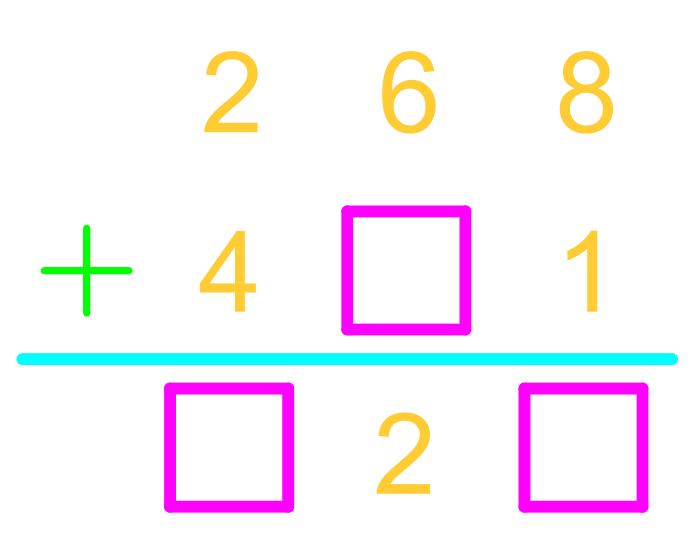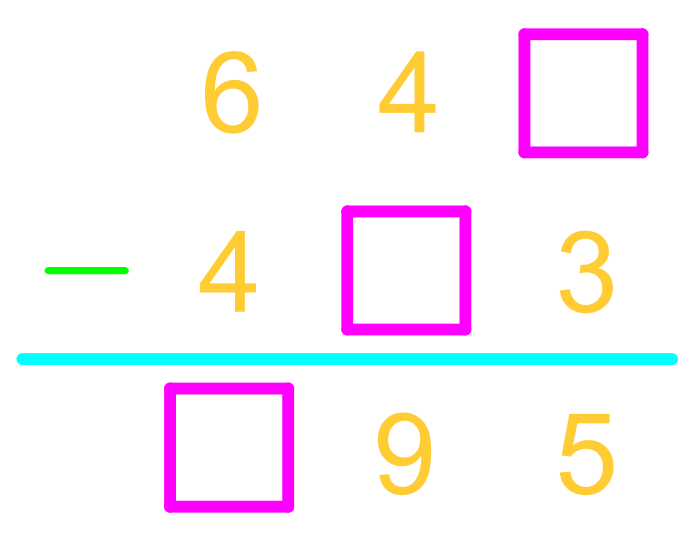Finding the Missing Digit: Unlock Your Math Potential

Discover powerful strategies to solve missing digit problems in addition and subtraction. Boost your numerical reasoning and computational skills with our comprehensive guide and engaging video lessons.

In this guide, we will walk through the process of finding missing digits in addition problems. This method ensures accuracy and eliminates the need for guessing. Follow the steps below to understand how to systematically approach these types of questions.

Step 1: Understand the Problem

First, carefully read the problem to understand what is being asked. In our example, we have an addition problem with missing digits. The problem is presented as follows:

330_ + 50_2 = _13

Our goal is to find the missing digits that make this equation true.

Step 2: Analyze Each Column

To solve the problem, we need to analyze each column of the addition problem individually. This helps us isolate the missing digits and solve for them step by step. We will start from the rightmost column and move to the left.

Step 3: Solve the Rightmost Column

Look at the rightmost column first. The equation here is:

_ + 2 = 3

To find the missing digit, we need to determine what number, when added to 2, equals 3. The answer is 1 because 1 + 2 = 3. Therefore, the missing digit in the rightmost column is 1.

Step 4: Solve the Middle Column

Next, we move to the middle column. The equation here is:

3 + _ = 1

At first glance, it seems impossible to find a number that, when added to 3, equals 1. This is because 3 is greater than 1. To resolve this, we need to consider carrying over a digit from the next column. We add 1 to the left of the 1, making it 11. Now the equation becomes:

3 + _ = 11

The missing digit is 8 because 3 + 8 = 11. Therefore, the missing digit in the middle column is 8.

Step 5: Solve the Leftmost Column

Finally, we move to the leftmost column. The equation here is:

1 + 3 + 5 = _

We need to find the sum of these numbers. Adding them together, we get:

1 + 3 = 4

4 + 5 = 9

Therefore, the missing digit in the leftmost column is 9.

Step 6: Verify the Solution

After finding all the missing digits, it's important to verify the solution by adding the numbers together to ensure the equation is correct. The completed equation should be:

3301 + 5082 = 8393

By verifying the solution, we can confirm that our method is accurate and the missing digits are correctly identified.

Conclusion

By following these steps, you can systematically find missing digits in addition problems. This method ensures accuracy and eliminates the need for guessing. Remember to analyze each column individually, consider carrying over digits when necessary, and always verify your solution.

1. What is the column strategy for finding missing digits?

   The column strategy is a systematic approach to solving addition and subtraction problems with missing digits. It involves analyzing each column of the problem individually, starting from the rightmost column and working towards the left. This method helps in logically deducing the missing digits by considering place values and carry-overs or borrowing when necessary.

2. How do you handle carry-over in addition problems with missing digits?

   When dealing with carry-over in addition problems, start from the rightmost column and work left. If the sum in a column exceeds 9, write down the ones digit and carry the tens digit to the next column. Continue this process, including any carried numbers from previous columns, until you reach the leftmost column. This technique is crucial for maintaining accurate place values in your calculations.

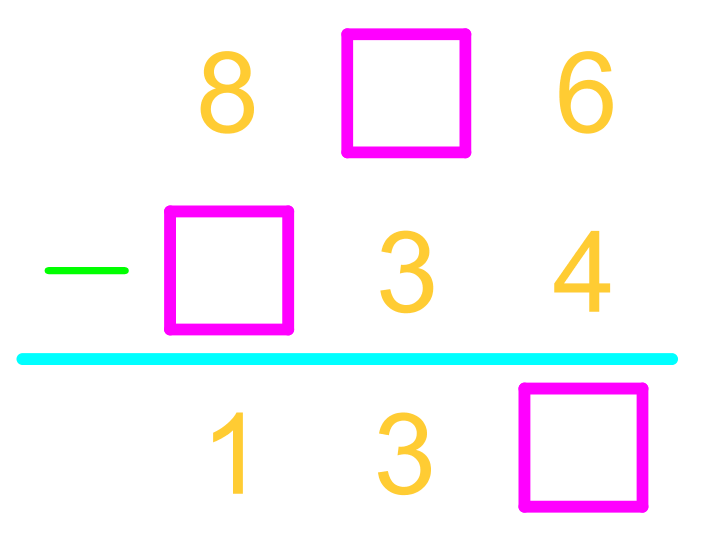
3. What's the difference between solving missing digit problems in addition versus subtraction?

   While both use the column strategy, subtraction problems often involve borrowing instead of carrying. In subtraction, you may need to borrow from higher place values when you can't subtract the bottom digit from the top digit. This process involves regrouping numbers to make the subtraction possible. Addition focuses on carrying excess values to the next column, while subtraction focuses on borrowing from higher place values.

4. What are some common challenges in solving missing digit problems?

   Common challenges include dealing with multiple missing digits, understanding place value, and recognizing when to borrow or carry over. Students may feel overwhelmed when faced with several unknowns or struggle to grasp the significance of each digit's position. Overcoming these challenges involves breaking down problems into smaller steps, using visualization techniques, and practicing borrowing and carrying exercises separately before integrating them into missing digit problems.

5. How can I improve my skills in solving missing digit problems?

   To improve your skills, practice regularly with a variety of problems, starting from simple ones and gradually increasing difficulty. Use visualization techniques like place value charts to better understand digit positions. Develop your logical thinking by asking yourself questions about how changing digits affects the overall result. Connect these problems to real-world scenarios to make them more relatable. Finally, maintain a growth mindset, viewing challenges as opportunities to learn and improve your mathematical abilities.

Understanding the foundation of mathematics is crucial when tackling more advanced concepts like finding the missing digit. Two key prerequisite topics that play a significant role in this area are place value and distance and time related questions in linear equations. These fundamental concepts provide the necessary groundwork for students to excel in more complex mathematical problems.

The place value system is an essential concept that forms the backbone of our number system. It helps students understand the significance of each digit's position in a number, which is crucial when identifying or calculating a missing digit. By mastering place value, students can easily recognize the impact of a missing digit on the overall value of a number, making it easier to deduce the correct answer.

Moreover, a solid grasp of place value enables students to perform mental math more efficiently, a skill that proves invaluable when working with missing digit problems. It allows for quick estimations and helps in narrowing down possible solutions, ultimately leading to more accurate and faster problem-solving.

While it might not seem immediately apparent, solving multi-digit subtraction problems, often encountered in distance and time related questions, is closely related to finding missing digits. These problems require students to work with multiple digits simultaneously, often involving borrowing or regrouping. This skill directly translates to scenarios where a digit is missing, as students need to consider the relationships between different place values and how they affect the overall calculation.

Furthermore, the logical thinking and problem-solving strategies developed while working on distance and time questions in linear equations can be applied to missing digit problems. Both types of problems often require a step-by-step approach, careful consideration of given information, and the ability to work backwards from a known result to find an unknown value.

By focusing on these prerequisite topics, students build a strong foundation that makes tackling missing digit problems much more manageable. The place value system provides the necessary understanding of number structure, while experience with multi-digit operations and linear equations hones the problem-solving skills required for more complex scenarios.

In conclusion, mastering these prerequisite topics is not just about learning isolated concepts; it's about building a interconnected web of mathematical knowledge. This comprehensive understanding allows students to approach missing digit problems with confidence, armed with the tools and strategies necessary for success. As students progress in their mathematical journey, they'll find that these foundational skills continue to play a crucial role in more advanced mathematical concepts, reinforcing the importance of thoroughly grasping these prerequisite topics.