Además de usar la pendiente, otro método sencillo para encontrar el número de soluciones de un sistema de ecuaciones lineales es graficándolo.
Al graficar las líneas provenientes de cada ecuación del sistema, se puede buscar por algún punto de intersección entre ellas y por la falta de éste y así determinar si el sistema tiene una solución, infinitas, o ninguna.
A un sistema de ecuaciones lineales con al menos una solución se le llama consistente, por otra parte, si el sistema no tienen ninguna solución se le llama inconsistente.
Una solución: En un sistema de ecuaciones lineales con una solución, las líneas correspondientes al sistema se interceptan en un punto en la gráfica. Este punto da el valor de cada una de las variables . Este sistema es consistente e independiente.
Soluciones infinitas: En un sistema de ecuaciones lineales con soluciones infinitas, las líneas correspondientes al sistema se superponen en cada uno de sus puntos (son la misma línea). A esto se le llama un sistema consistente y dependiente.
Sin solución: En un sistema de ecuaciones lineales sin solución, las líneas correspondientes al sistema son paralelas entre sí. A esto se le llama un sistema inconsistente.
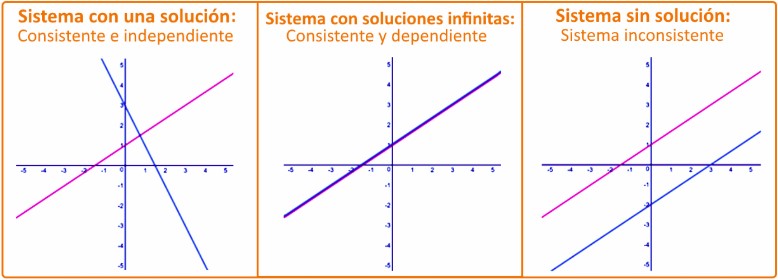
Una solución: En un sistema de ecuaciones lineales con una solución, las líneas correspondientes al sistema se interceptan en un punto en la gráfica. Este punto da el valor de cada una de las variables . Este sistema es consistente e independiente.
Soluciones infinitas: En un sistema de ecuaciones lineales con soluciones infinitas, las líneas correspondientes al sistema se superponen en cada uno de sus puntos (son la misma línea). A esto se le llama un sistema consistente y dependiente.
Sin solución: En un sistema de ecuaciones lineales sin solución, las líneas correspondientes al sistema son paralelas entre sí. A esto se le llama un sistema inconsistente.







