Si el área de la sección transversal de un sólido se define como = , entonces:
Dado un sólido con una base modelada por y con una figura en su sección transversal conocida, podemos definir su volumen con lo siguiente:
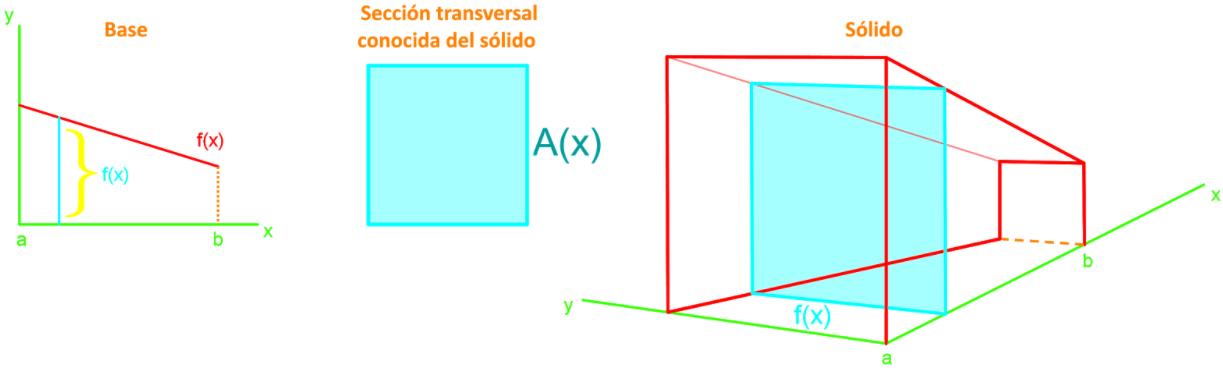
Dado un sólido con una base modelada por y con una figura en su sección transversal conocida, podemos definir su volumen con lo siguiente:







