Sign In
Join for Free
 flag-us

Coordenadas polares

Now Playing:Es polar coordinates – Example 1a
Examples
  1. Convirtiendo Ecuaciones Cartesianas a Coordenadas polares
    Convierte las siguientes ecuaciones cartesianas a coordenadas polares:
    1. x2+y2=5x^2+y^2=5

    2. x2+4x+y2+4y+8=(tan⁡−1yx)2x^2+4x+y^2+4y+8=(\tan^{-1} \frac{y}{x})^2

    3. x2−y3=6 x^2-y^3=6

Coordenadas polares
Jump to:Notes
Notes
En esta sección introduciremos un nuevo sistema de coordenadas llamado el Sistema Polar o Sistema de Coordenadas Polares.

Por el momento nos enfocaremos en convertir coordenadas polares a coordenadas cartesianas, coordenadas cartesianas a polares y construir ecuaciones polares.

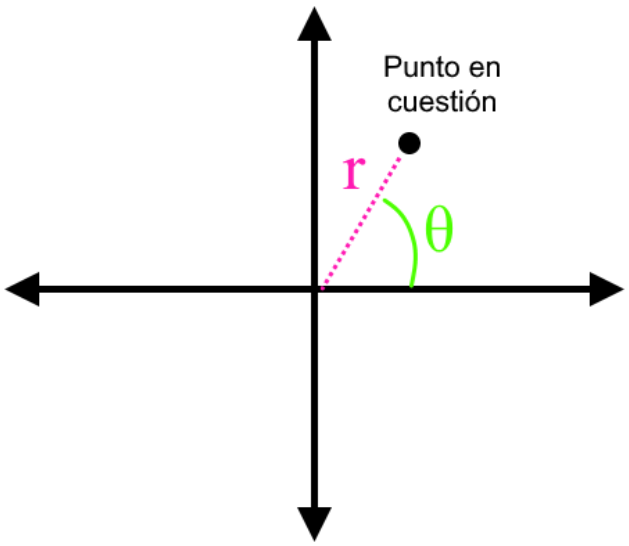
En coordenadas cartesianas el par ordenado que define las coordenadas de un punto se escribe como (x,y)(x, y). En coordenadas polares se utilizan las variables r r \, y  θ\,\theta , donde rr significa “radio” (la distancia desde el origen al punto en cuestión) y  θ \, \theta \, es el ángulo con respecto al eje xx. Por lo tanto, el par ordenado de coordenadas se escribe como (r,θ)(r, \theta).

Basics of Coordinate Plane

Cuando convertimos de coordenadas polares a coordenadas cartesianas podemos utilizar las siguientes fórmulas:

x=rcos⁡θx=r \cos \theta
y=r sen θy=r \, sen \, \theta
r2=x2+y2r^2=x^2+y^2
r=x2+y2r=\sqrt{x^2+y^2}
θ=tan⁡−1(yx)\theta = \tan^{-1}(\frac{y}{x})